Алгоритм RSK, плоские разбиения и симметрические функции

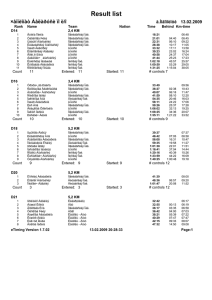
Àëãîðèòì RSK, ïëîñêèå ðàçáèåíèÿ è
ñèììåòðè÷åñêèå ôóíêöèè
The RSK Algorithm, Plain Partitions and Symmetric
Functions
Äëÿ 1 êóðñà
Ïîëèíà Ôèëèïïîâà, e-mail: [email protected]; vk.com/apolylav
Àëãîðèòì Ðîáèíñîíà-Øåíñòåäà-Êíóòà (àëãîðèòì RSK) îñóùåñòâëÿåò áèåêöèþ ìåæäó ìàòðèöàìè ñ íåîòðèöàòåëüíûìè öåëûìè êîýôôèöèåíòàìè
è óïîðÿäî÷åííûìè ïàðàìè ïîëóñòàíäàðòíûõ òàáëèö Þíãà îäíîé ôîðìû. Âàæíûé øàã ýòîãî àëãîðèòìà òàê íàçûâàåìàÿ ñòðî÷íàÿ âñòàâêà,
èëëþñòðèðóåìàÿ êàðòèíêîé íèæå.
Êóðñîâàÿ ðàáîòà ñîñòîèò â òîì, ÷òî áû ðàçîáðàòü ýòîò àëãîðèòì è
ïîíÿòü, êàê ñ åãî ïîìîùüþ âûâîäèòñÿ ðÿä òîæäåñòâ äëÿ ñèììåòðè÷åñêèõ ôóíêöèé è ïðîèçâîäÿùàÿ ôóíêöèþ äëÿ ÷èñëà ïëîñêèõ ðàçáèåíèé
Ýòî ïîìîæåò ïðèîáðåñòè íàâûêè ðàáîòû ñ ñèììåòðè÷åñêèìè ôóíêöèÿìè è ñ äèàãðàììàìè è òàáëèöàìè Þíãà îáúåêòàìè, êîòîðûå èãðàþò
çàìåòíóþ ðîëü â òåîðèè ïðåäñòàâëåíèé è äðóãèõ îáëàñòÿõ ñîâðåìåííîé
ìàòåìàòèêè.
1 223 4
1 2 2 33
2 335
2 3 34
=
3
45
4 6
56
5
6
6
Ëèòåðàòóðà
Ñòåíëè Ð. Ïåðå÷èñëèòåëüíàÿ êîìáèíàòîðèêà. Äåðåâüÿ, ïðîèçâîäÿùèå
ôóíêöèè è ñèììåòðè÷åñêèå ôóíêöèè: Ïåð. ñ àíãë. Ì.: Ìèð, 2009. Òîì
2., ãëàâà 7 ¾Ñèììåòðè÷åñêèå ôóíêöèè¿.
Ñêîðåå âñåãî, ïðîèçâîäÿùèå ôóíêöèè íà îñíîâíûõ êóðñàõ áóäóò ïðîõîäèòü ïîçæå, ÷åì îíè ïîíàäîáÿòñÿ â êóðñîâîé ðàáîòå, è ïðî íèõ ïðè
íåîáõîäèìîñòè ìîæíî ïðî÷èòàòü â òîé æå êíèãå èëè â êíèãå: Ëàíäî Ñ.Ê.
Ââåäåíèå â äèñêðåòíóþ ìàòåìàòèêó. Ì.: ÌÖÍÌÎ, 2012.