Момент импульса частицы относительно точки

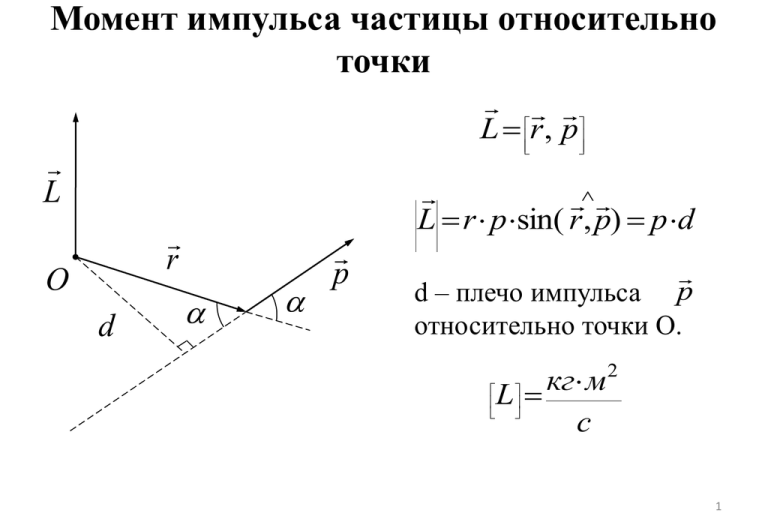
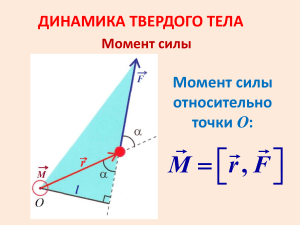
Момент импульса частицы относительно
точки
  
L  r , p

L

^ 
L  r  p sin( r , p)  p d

r
O
d



p

d – плечо импульса p
относительно точки О.



L  кг м
с
2
1
Момент силы относительно точки
  
M  r , F 



^ 
M  r  F sin( r ,F)  F d

M

r
O
d



F

d – плечо силы F
относительно точки О.



M   Н  м
2
Уравнение моментов
dL  r

 dp 
r , F 
  , p   r ,

v
,
p





dt
dt 
 dt



0, т.к. v  p
 
dL  M
dt
3
Вращение системы материальных точек
вокруг точки. Уравнение моментов.


Lсистемы   Li


dLсистемы
  M внутренних
сил
dt
i
i


  M внешних   M внешних
i
сил
0 ( Fik параллелен rik )

Fik

Fki
i
сил
Момент импульса частицы относительно оси

p
r   e  rz ez
p  p e   p e  pz ez
Z
pz
p
rz
O
e
ez


r
e
p
e
L 
p
e
0
p
ez
rz
pz
Lz   p  m 2 z
   z
5
Момент силы, действующий на частицу,
относительно оси.

F
F  F e   F e  Fz ez
Z
Fz
F
rz
O
r   e  rz ez
e
ez


r
e
F
e
M 
F
e
0
F
ez
rz
Fz
M z   F
6
Момент инерции твёрдого тела
mi
I   mi ri2
ri
i
I   r dm
2
M
Пример: Вычислим I0 стержня массой m и длинной l.
m
dm dx
l
dx
ц.м.
l
2
0
l
x
l
2
X
2
2m
2
ml
I 0   x dx 
l
12
l
2
7
Вращение твёрдого тела вокруг неподвижной
оси














Lz   mi  i z
i
I – момент инерции
dLz
d z
Mz 
I 
 I  z
dt
dt
z

M 



F
Для главных осей:


L  I 
8
Теорема Штейнера
I0
m
I
I  I 0  mx 2
цм
x
Пример: Вычислим I стержня массой m и длинной l.
2
Центральный момент
инерции
ml
I0 
12
цм
I
I0






2





l
ml
I  I0  m

2
3
2
Момент пары сил

F1

r12
2

r2
1 
r1
O

F2

 F1
r12
O

F2
 
F1  F2
  


M  r1 ,F1   r2 ,F2  

 







  r1  r2 ,F1    r2  r1 ,F2  

 




 
 r12 ,F1   r21 ,F2 




Если силы направлены вдоль
одной прямой:

M 0
10
Кинетическая энергия вращения твёрдого
тела вокруг оси.
 ( m i ri ) 
2
miv
Eк  
2
i
2
i

2
i
2


r
v
I

2
2
Кинетическая энергия при плоском движении
твёрдого тела.
mv
Eк 
2
2
c

I 0
2
2
Пример: Однородный шар массой m и радиусом R
катится со скоростью . v
v
m
R
mv
Eк 
2
2
2
7
2 
2
 mR

mv
5
2
10
2