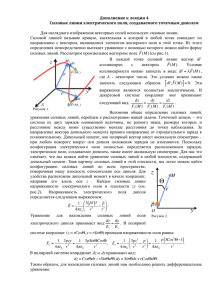
Семинар 6. Картина силовых линий. Распределение

Семинар 6. Картина силовых линий. Распределение
электрического потенциала.
Картина силовых линий
Разработайте компьютерную программу для изображения на плоскости силовых линий системы
электрических зарядов. Предусмотрите возможность варьирования величины и знака зарядов, их
общего количества и местоположения на плоскости.
Теория.
Напряженность электрического поля системы n точечных зарядов.
r r
n
r r
qi (r − ri )
Визуализация. Наглядное изображение. Силовые линии. Направление вектора
E (r ) = k ∑ r
3
i =1 r − ri
напряженности электрического поля – по касательной к силовым линиям.
y
Силовые линии: начинаются на положительных зарядах и
кончаются на отрицательных или уходят на бесконечность.
Число линий пропорционально заряду.
x
Алгоритм построения силовых линий.
Введем декартову систему координат (x, y).
r
Т.к. вектор E направлен по касательной к силовым линиям, то
уравнение траектории силовой линии имеет вид:
dх E x
dy E y
=
=
(1) или
(2).
dx E x
dy E y
Уравнения (1) и (2) служат основой для расчета силовых линий. Расчет силовой линии начинается в
окрестности положительного заряда. Соответственно задаются начальные условия (x0, y0). Вместе с
начальными условиями уравнение (1) или (2) являются задачей Коши, которая может быть решена с
помощью численных методов решения ОДУ, например, используя схему Эйлера или Рунге-Кутта.
Полученное решение отображается графически.
Особенности.
1. Для построения (расчета) силовой линии используется одно из уравнений (1) или (2) в зависимости от
поведения знаменателя. При стремлении знаменателя к нулю (силовая линия горизонтальная или
вертикальная) следует продолжить расчет, используя другое уравнение.
2. Для поддержания большей густоты силовых линий в области больших величин напряженности можно
выбирать число начальных точек (количество силовых линий) в окрестности положительного заряда
пропорционально величине этого заряда.
3. При наличии видимых изломов силовых линий следует уменьшить шаг интегрирования и построить
эти линии заново.
Варианты начальных условий. Точечный заряд. Два точечных заряда. Симметричный квадруполь.
Модель плоского конденсатора. Случайно расположенные заряды со случайной величиной и знаком.
Выбор количества зарядов, их знаков, величин и положения на плоскости на усмотрение пользователя
(средствами интерфейса прикладной программы).
Вариант задания. Построение эквипотенциалей системы точечных электрических зарядов на плоскости
(самостоятельно). Намек: эквипотенциальные поверхности перпендикулярны силовым линиям. Важно:
необходимо отображать величину потенциала и его знак (например, цветом).
Литература
1. И.В. Савельев. Курс общей физики. М.: Наука, 1973, т. 2, глава 1.
2. А.Н. Матвеев. Электричество и магнетизм. М.: Высшая школа, 1983, главы 1-2
2
Распределение электрического потенциала
На каждой из четырех границ прямоугольной области поддерживается свой собственный
постоянный электрический потенциал. Найдите распределение электрического потенциала внутри
прямоугольной области.
Численное решение уравнения Лапласа методом релаксаций.
Пусть ϕ - потенциал электростатического поля. Тогда
∆ϕ = 0
Граничные условия
ϕ Г = ϕГ1 , ϕ Г2 , ϕ Г3 , ϕГ4 .
r
Напряженность электрического поля E = - ∇ϕ .
(1).
В декартовой системе координат (1) принимает вид:
∂ϕ ∂ϕ
+
=0
∂x 2 ∂y 2
(2)
Введем расчетную сетку с узлами (i,j) в указанной
прямоугольной
области.
Пусть
∆x = ∆y = h
(эквидистантная квадратная сетка). Аппроксимируем
производные конечными разностями:
ϕ i +1, j − ϕ i , j
∂ϕ
≈
h
∂x i , j
(3)
Аналогично аппроксимируем производную по y.
Вторую производную аппроксимируем центральной
разностью:
∂ ϕ
≈
∂x 2 i , j
2
∂ϕ
∂ϕ
−
∂x i , j ∂x i −1, j
h
=
ϕ i +1, j − ϕ i , j − (ϕ i , j − ϕ i −1, j )
h
2
=
ϕ i +1, j − 2ϕ i , j + ϕ i −1, j
h2
ϕ i , j +1 − 2ϕ i , j + ϕ i , j −1
∂ 2ϕ
≈
∂x 2 i , j
h2
(4)
(5)
Подставляем (4), (5) в (2). Получаем:
ϕi, j =
ϕ i +1, j + ϕ i −1, j + ϕ i , j +1 + ϕ i , j −1
4
.
(6)
Возник шаблон типа «крест», в соответствие с которым значение функции во внутренней точки области
равно среднему арифметическому по ближайшим «соседям». Для того, чтобы удовлетворить граничным
условиям положим: ϕ 0, j = ϕ Г1 , ϕ i , N −1 = ϕ Г2 , ϕ N −1, j = ϕ Г3 , ϕ i , 0 = ϕ Г4 , где N – число узлов по каждой
координате.
Как найти ϕ i, j , если значения всех соседей неизвестно? Метод релаксации (итераций). Предположим,
что значения во всех точках известны. Назовем это нулевой итерацией ϕ i , j . Тогда подставив эти
(0)
значения в правую часть (6), найдем значения в узлах сетки на первой итерации и т.д. В общем случае
значения потенциала в узлах расчетной сетки на n-ой итерации ϕ i , j выражаются через значения на
(n)
предыдущей итерации следующим образом:
ϕ i(,nj) =
ϕ ( n −1) i +1, j + ϕ ( n −1) i −1, j + ϕ ( n −1) i , j +1 + ϕ ( n −1) i , j −1
4
(7)
Формула (7) – основная расчетная формула метода релаксаций. Нулевая итерация во внутренних точках
расчетной сетки может быть выбрана произвольно. На каждом итерационном шаге граничные условия
выполняются, меняются значения только внутренних точек. Итерационный алгоритм сходится.
3
( n −1)
Критерий завершения итерационного процесса Max ϕ i , j − ϕ i , j
( n)
i, j
< ε.
Цели. Различные граничные условия. Различное число узлов сетки. Визуализация итерационного
процесса решения графическими средствами (цветовые карты распределения потенциала). Выбор
нулевой итерации: ϕ i , j = 0 , ϕ i , j = (ϕ Г1 + ϕ Г2 + ϕ Г3 + ϕ Г4 ) 4 , другой вариант. Анализ сходимости
(0)
(0)
решения в зависимости от выбора нулевой итерации.
Вариант. Включение в центр области круга с заданным потенциалом ϕ Г5 . Аппроксимация граничных
условий на прямоугольной сетке.
Литература
1. А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука, 1989