определение момента и межатомного расстояния молекулы

Ëàáîðàòîðíàÿ ðàáîòà ¹72
ÎÏÐÅÄÅËÅÍÈÅ ÌÎÌÅÍÒÀ È ÌÅÆÀÒÎÌÍÎÃÎ
ÐÀÑÑÒÎßÍÈß ÌÎËÅÊÓËÛ ÖÈÀÍÀ (ÏÎËÎÑÀ ÑN).
ÂÂÅÄÅÍÈÅ.
I.Îïûòíûå äàííûå.
Ìîëåêóëÿðíûå ñïåêòðû ìîæíî îáíàðóæèòü â ñâå÷åíèè ðàçëè÷íûõ
âèäîâ ãàçîâîãî ðàçðÿäà, ïëàìåíè, ôëþîðåñöåíöèè. Íàáëþäàåìûå ñ ïîìîùüþ
ïðèáîðîâ ñ íåáîëüøîé äèñïåðñèåé ìîëåêóëÿðíûå ñïåêòðû èìåþò âèä ïîëîñ.
Ýòè ïîëîñû îáû÷íî ñ îäíîé ñòîðîíû îãðàíè÷åíû ðåçêèì êðàåì êàíòîì, ñ
äðóãîé èíòåíñèâíîñòü ïîñòåïåííî ñïàäàåò äî íóëÿ. Ýòîò ïîñòåïåííûé ñïàä
èíòåíñèâíîñòè íàçûâàþò "îòòåíåíèåì". Ðàçëè÷àþò "êðàñíîå" è "ôèîëåòîâîå"
îòòåíåíèå â çàâèñèìîñòè îò åãî ðàñïîëîæåíèÿ ñî ñòîðîíû äëèííûõ èëè
êîðîòêèõ âîëí ñîîòâåòñòâåííî. Èíîãäà ïîëîñû èìåþò íåñêîëüêî êàíòîâ, â
íåêîòîðûõ ñëó÷àÿõ êàíòû ñîâñåì îòñóòñòâóþò.
Ïîëîñû, îáëàäàþùèå ðÿäîì îáùèõ ñâîéñòâ: îäíîâðåìåííîå ïîÿâëåíèå,
ëîêàëèçàöèÿ â îïðåäåëåííîé ÷àñòè ñïåêòðà, îäèíàêîâîå îòòåíåíèå, îäèíàêîâîå
÷èñëî êàíòîâ - îáúåäèíÿþòñÿ â ñèñòåìû.
Ïðèáîðàìè ñ áîëüøîé ðàçðåøàþùåé ñèëîé áîëüøèíñòâî ïîëîñ
ðàçðåøàåòñÿ íà îòäåëüíûå ëèíèè, ðàññòîÿíèå ìåæäó êîòîðûìè ïîñòåïåííî
óâåëè÷èâàåòñÿ ïî ìåðå óäàëåíèÿ îò êàíòà. Îäíàêî, âñòðå÷àþòñÿ è ñïëîøíûå
ìîëåêóëÿðíûå ñïåêòðû. Ñïåêòðû ïîãëîùåíèÿ ìîëåêóë ãîðàçäî áåäíåå
ýìèññèîííûõ ñïåêòðîâ.  îáëàñòè äîñòàòî÷íî êîðîòêèõ âîëí âñåãäà
íàáëþäàåòñÿ ñïëîøíîå ïîãëîùåíèå, êîòîðîå ïðèìûêàåò ê ñåðèè ïîëîñ.
II. Îñíîâû òåîðèè äâóõàòîìíûõ ìîëåêóë.
Êâàíòîâàÿ òåîðèÿ õîðîøî îáúÿñíÿåò âñå îñîáåííîñòè ñòðîåíèÿ ñïåêòðîâ
äâóõàòîìíûõ ìîëåêóë. Òåîðèÿ ñïåêòðîâ ìíîãîàòîìíûõ ìîëåêóë çíà÷èòåëüíî
ñëîæíåå, îíà åùå íå ïîëíîñòüþ ðàçðàáîòàíà è ñåé÷àñ íàõîäèòñÿ â ñòàäèè
ðàçâèòèÿ.
 äàëüíåéøåì ìû áóäåì ðàññìàòðèâàòü òîëüêî äâóõàòîìíûå ìîëåêóëû. Â
ìîëåêóëàõ àòîìû ñâÿçàíû ñèëàìè âçàèìíîãî ïðèòÿæåíèÿ. Ðàçëè÷èÿ â ïðèðîäå
ýòèõ ñèë ïîëîæåí â îñíîâó êëàññèôèêàöèè ìîëåêóëÿðíûõ ñâÿçåé. Óêàæåì íà
äâà îñíîâíûõ âèäà ñâÿçåé: ãîìåîïîëÿðíóþ è ãåòåðîïîëÿðíóþ. Ïîñëåäíÿÿ èìååò
ìåñòî, íàïðèìåð, ó ùåëî÷íî-ãàëîèäíûõ ñîåäèíåíèé.
Àòîìû ùåëî÷íûõ ýëåìåíòîâ îáëàäàþò íèçêèì ïîòåíöèàëîì èîíèçàöèè. Îíè
ëåãêî îòäàþò ñâîé âàëåíòíûé ýëåêòðîí àòîìó ãàëîèäà, èìåþùåìó ñèëüíîå
ýëåêòðîííîå ñðîäñòâî. Îáðàçóþùèåñÿ òàêèì îáðàçîì èîíû ïðèòÿãèâàþòñÿ
äðóã ê äðóãó ýëåêòðîñòàòè÷åñêèìè ñèëàìè. Ìîëåêóëû ýòîãî âèäà îáëàäàþò
áîëüøèì ýëåêòðè÷åñêèì äèïîëüíûì ìîìåíòîì. Ýíåðãèþ èîííîé ñâÿçè ìîæíî
ðàññ÷èòàòü íà îñíîâå êëàññè÷åñêèõ ïðåäñòàâëåíèé.  ñëó÷àå ãîìåîïîëÿðíûõ
ìîëåêóë ( H 2 , N 2 , O2 ) áîëüøàÿ ýíåðãèÿ ñâÿçè ìîæåò áûòü îáúÿñíåíà òîëüêî ñ
ïîìîùüþ êâàíòîâîé òåîðèè, ñîãëàñíî êîòîðîé âçàèìíîå ïðèòÿæåíèå
äâóõàòîìíûõ ìîëåêóë îáóñëîâëåíî, òàê íàçûâàåìûìè, îáìåííûìè ñèëàìè, íå
èìåþùèå êëàññè÷åñêîãî àíàëîãà. Äëÿ îáðàçîâàíèÿ ãîìåîïîëÿðíîé ñâÿçè
1
Ëàáîðàòîðíàÿ ðàáîòà ¹72
îáÿçàòåëüíî íàëè÷èå ó àòîìîâ ýëåêòðîíîâ ñ íåêîìïåíñèðîâàííûìè ñïèíîâûìè
ìîìåíòàìè. Óñòîé÷èâîå ñîñòîÿíèå âîçíèêàåò òîëüêî ïðè îáúåäèíåíèè àòîìîâ
ñ ïðîòèâîïîëîæíûìè ñïèíîâûìè ìîìåíòàìè. Ó áîëüøèíñòâà ìîëåêóë èîííîå
è îáìåííîå âçàèìîäåéñòâèå ïðîÿâëÿåòñÿ îäíîâðåìåííî.
Ïîòåíöèàëüíàÿ ýíåðãèÿ ìîëåêóë, ðàññìàòðèâàåìàÿ êàê ôóíêöèÿ ìåæàòîìíîãî
ðàññòîÿíèÿ, â ñëó÷àå ôèçè÷åñêè óñòîé÷èâîãî ñîñòîÿíèÿ îáÿçàòåëüíî äîëæíà
èìåòü ìèíèìóì. Ýòó ôèçè÷åñêóþ óñòîé÷èâîñòü ñëåäóåò îòëè÷àòü îò õèìè÷åñêîé
óñòîé÷èâîñòè. Íàïðèìåð, ìîëåêóëû CN , CH , OH è ðÿä äðóãèõ îáëàäàþò
ôèçè÷åñêîé óñòîé÷èâîñòüþ, íî ïðè îáû÷íîé òåìïåðàòóðå äîëãî ñóùåñòâîâàòü
íå ìîãóò, à â ïëàìåíè äóãè íåïðåðûâíî âîçíèêàþò: îíè âñòóïàþò â õèìè÷åñêóþ
ðåàêöèþ, îáðàçóÿ õèìè÷åñêè óñòîé÷èâûå ñîåäèíåíèÿ. Èõ ñóùåñòâîâàíèå ìîæíî
îáíàðóæèòü òîëüêî îïòè÷åñêèì ìåòîäîì ïî õàðàêòåðíûì äëÿ íèõ ñïåêòðàì.
Ïðè îáðàçîâàíèè ìîëåêóëû èç âíåøíèõ ýëåêòðîííûõ îáîëî÷åê àòîìîâ
âîçíèêàåò îáîëî÷êà ìîëåêóëû, êîòîðàÿ ñèììåòðè÷íà â ñëó÷àå ñèììåòðè÷íûõ
ìîëåêóë ( H 2 , N 2 , O2 ) è íå ñèììåòðè÷íà ó ãåòåðîïîëÿðíûõ.
Âíóòðåííèå îáîëî÷êè àòîìîâ ïðè ýòîì ñóùåñòâåííî íå èçìåíÿþòñÿ. Â
ñîîòâåòñòâèè ñ ðàçäåëåíèåì ìîëåêóëÿðíûõ ñïåêòðîâ íà ñèñòåìû, ñèñòåì íà
ïîëîñû, à ïîëîñ íà îòäåëüíûå ëèíèè, âíóòðåííþþ ýíåðãèþ ìîëåêóëû ìîæíî
ðàçäåëèòü íà òðè, â ïåðâîì ïðèáëèæåíèè íåçàâèñèìûå ÷àñòè: ýíåðãèþ
ýëåêòðîííîé îáîëî÷êè, ýíåðãèþ êîëåáàíèÿ, ýíåðãèþ âðàùåíèÿ ìîëåêóë, êàê
öåëîãî.
Ñîãëàñíî êâàíòîâîé ìåõàíèêå, âñå ïåðå÷èñëåííûå âèäû ýíåðãèè êâàíòóþòñÿ
ò.å. ìîãóò ïðèíèìàòü äèñêðåòíîå çíà÷åíèå.
Âðàùàòåëüíîå äâèæåíèå.
Äëÿ âðàùàòåëüíîé ýíåðãèè ìîëåêóëû, â ïðåäïîëîæåíèè, ÷òî îíà ñîñòîèò èç
äâóõ òî÷å÷íûõ ìàññ, ñêðåïëåííûõ æåñòêîé íåâåñîìîé ñâÿçüþ (æåñòêèé ðîòàòîð),
êâàíòîâàÿ ìåõàíèêà äàåò ñëåäóþùåå âûðàæåíèå:
h2
E =
j( j + 1) = B h c j( j + 1 )
8π2J
(1)
ãäå J - ìîìåíò èíåðöèè ìîëåêóëû, j - âðàùàòåëüíîå êâàíòîâîå ÷èñëî,
j = 0 , 1, 2,K , c - ñêîðîñòü ñâåòà â âàêóóìå, h - ïîñòîÿííàÿ Ïëàíêà.
h
(2)
8 π 2 Jc
íàçûâàåòñÿ âðàùàòåëüíîé ïîñòîÿííîé ìîëåêóëû. Ïåðåõîä èç ñîñòîÿíèÿ E ′
â ñîñòîÿíèå ñ ìåíüøåé ýíåðãèåé E ′′ ñîãëàñíî îñíîâíîìó ñîîòíîøåíèþ ÷àñòîò
Áîðà E ′ − E ′′ = hν ñîïðîâîæäàåòñÿ èçëó÷åíèåì, ÷àñòîòà êîòîðîãî ñ ó÷åòîì
íàëàãàåìîãî êâàíòîâîé ìåõàíèêîé îãðàíè÷åíèÿ íà èçìåíåíèå ÷èñëà
j = 0 , 1, 2,K , ∆j = j ′′ − j ′ = ±1 âûðàçèòñÿ òàê:
Âåëè÷èíà
B=
∆ ν ñ ì −1 = 2 B ( j + 1)
2
(3)
 ôîðìóëå (3) è â äàëüíåéøåì ÷àñòîòà èçìåðÿåòñÿ â âîëíîâûõ ÷èñëàõ,
Ëàáîðàòîðíàÿ ðàáîòà ¹72
óêàçûâàþùèõ êàêîå ÷èñëî âîëí óêëàäûâàåòñÿ â îäíîì ñì. Òàê êàê ìîëåêóëà íà
ñàìîì äåëå íå ÿâëÿåòñÿ æåñòêîé ñèñòåìîé, åå ìîìåíò èíåðöèè äîëæåí çàâèñåòü
îò ÷àñòîòû âðàùåíèÿ. Ó÷åò ýòîãî ÿâëåíèÿ ïðèâîäèò â âûðàæåíèè (1) ê ìàëîé
ïîïðàâêå, êîòîðîé ìû â äàëüíåéøåì áóäåì ïðåíåáðåãàòü. Êàê âèäíî èç ôîðìóëû
(3), âðàùàòåëüíûé ñïåêòð ìîëåêóëû â ïðèíÿòîì ïðèáëèæåíèè ñîñòîèò èç
ðÿäà ðàâíîñòîÿùèõ ëèíèé. Òàê êàê âðàùàòåëüíàÿ ýíåðãèÿ ìîëåêóëû
îòíîñèòåëüíî ìàëà, ýòîò ñïåêòð äîëæåí ðàñïîëàãàòüñÿ â äàëåêîé èíôðàêðàñíîé
îáëàñòè. Äåéñòâèòåëüíî â ýòîé îáëàñòè ó äèïîëüíûõ ìîëåêóë íàáëþäàåòñÿ
ñåëåêòèâíîå ïîãëîùåíèå â âèäå ïî÷òè ðàâíîñòîÿùèõ â øêàëå ÷àñòîò ëèíèé.
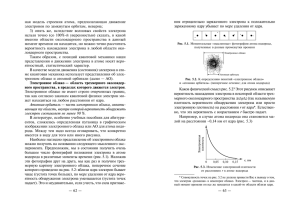
Ðèñ.1. Óðîâíè ýíåðãèè è èíôðàêðàñíûå ïåðåõîäû æåñòêîãî ðîòàòîðà.
à) äèàãðàììà óðîâíåé ýíåðãèè,
á) ñïåêòð æåñòêîãî ðîòàòîðà (ñõåìàòè÷åñêèé)
Ïîãëîùåíèå %
Íà ðèñ.1 ñõåìàòè÷åñêè ïîêàçàíà ñõåìà óðàâíåíèé è ñïåêòð æåñòêîãî
ðîòàòîðà, íà ðèñ.2 èçîáðàæåí ó÷àñòîê ýêñïåðèìåíòàëüíîãî íàáëþäàåìîãî
ñïåêòðà ïîãëîùåíèÿ ìîëåêóëû HCl .
100
80
3,8
3,7
3,6
3,5
3,4
60
34
40
2
4'
3'
2'
20
1
1'
6' 5'
0
8'ρ7'
9'
R
12' 11' 10'
20
Ðèñ.2.
3
Ëàáîðàòîðíàÿ ðàáîòà ¹72
Îðäèíàòû äàþò ïðîöåíò ïðîïóñêàåìîãî ñâåòà. Ìîìåíòû èíåðöèè è
ìåæàòîìíûå ðàññòîÿíèÿ, îïðåäåëÿåìûå íà îñíîâå òàêèõ ñïåêòðîâ ïî ôîðìóëàì
(2) è (3) õîðîøî ñîãëàñóþòñÿ ñ ðåçóëüòàòàìè äðóãèõ ìåòîäîâ.
Ñèììåòðè÷íûå ìîëåêóëû, íå èìåþùèå ïîñòîÿííîãî äèïîëüíîãî ìîìåíòà, â
äàëåêîé èíôðàêðàñíîé îáëàñòè íå èçëó÷àþò è íå ïîãëîùàþò.
Êîëåáàòåëüíîå äâèæåíèå.
Ðàññìàòðèâàÿ êîëåáàòåëüíîå äâèæåíèå ìîëåêóëû, áóäåì ñíà÷àëà ïðåäïîëàãàòü,
÷òî êîëåáàíèÿ ìàëû è ïîòîìó ñèëó, âîçâðàùàþùóþ àòîìû ê ïîëîæåíèþ
ðàâíîâåñèÿ, ìîæíî ñ÷èòàòü êâàçè óïðóãîé, ëèíåéíî çàâèñÿùåé îò îòêëîíåíèÿ:
f = − k ∆x
Ñèñòåìà, óäîâëåòâîðÿþùàÿ ýòîìó óñëîâèþ, íàçûâàåòñÿ ãàðìîíè÷åñêèì
îñöèëëÿòîðîì.
Äëÿ åãî ýíåðãèè êâàíòîâàÿ ìåõàíèêà äàåò ñëåäóþùåå âûðàæåíèå:
E êîë = hnêë ( u + 12 )
(4)
1 k
, ãäå k ãäå υ êîëåáàòåëüíîå êâàíòîâîå ÷èñëî, υ = 0 , 1, 2,K, νêë =
2π µ
óïðóãàÿ êîíñòàíòà ñâÿçåé, µ - ïðèâåäåííàÿ ìàññà ìîëåêóëû.
Âåëè÷èíà νêë ñîâïàäàåò ñ ñîáñòâåííîé êëàññè÷åñêîé ÷àñòîòîé ìîëåêóëû. Èç
ôîðìóëû (4) âèäíî, ÷òî äàæå â íèçêîì ýíåðãåòè÷åñêîì ñîñòîÿíèè, êîãäà υ = 0 ,
êîëåáàòåëüíàÿ ýíåðãèÿ E = 12 hνêë - ýòî íàèìåíüøàÿ ýíåðãèÿ, ñîâìåñòèìàÿ ñ
ñîîòíîøåíèåì íåîïðåäåëåííîñòè Ãåéçåíáåðãà.
Êâàíòîâàÿ ìåõàíèêà îãðàíè÷èâàåò ÷èñëî ðàçðåøåííûõ ïåðåõîäîâ ìåæäó
ðàçëè÷íûìè êîëåáàòåëüíûìè ñîñòîÿíèÿìè óñëîâèåì ∆υ = υ′′ − υ′ = ±1 .
Ïîýòîìó, ãàðìîíè÷åñêèé îñöèëëÿòîð, êàê ïî êëàññè÷åñêîé, òàê è ïî êâàíòîâîé
νêë
.
c
Äëÿ òîãî ÷òîáû èçëó÷åíèå (ïîãëîùåíèå) íà ñàìîì äåëå èìåëî ìåñòî, ïî
êëàññè÷åñêîé òåîðèè âî âðåìÿ êîëåáàíèÿ äîëæåí ìåíÿòüñÿ äèïîëüíûé ìîìåíò
ñèñòåìû, à ïî êâàíòîâîé äîëæíû áûòü îòëè÷íû îò íóëÿ ñîîòâåòñòâóþùèå
ìàòðè÷íûå ýëåìåíòû äèïîëüíîãî ïåðåõîäà.
òåîðèè ìîæåò èçëó÷àòü (ïîãëîùàòü) òîëüêî îäíó ÷àñòîòó
ω ñì =
−1
Ìîëåêóëà, êàê àíãàðìîíè÷åñêèé îñöèëëÿòîð.
Êîëåáàòåëüíàÿ ýíåðãèÿ ìîëåêóëû ïðèìåðíî íà ïîðÿäîê áîëüøå åå
âðàùàòåëüíîé ýíåðãèè, êîëåáàòåëüíûå ñïåêòðû ðàñïîëîæåíû â áëèæàéøåé
èíôðàêðàñíîé îáëàñòè è ñîñòîÿò, åñëè îòâëå÷üñÿ îò èõ òîíêîé ñòðóêòóðû, èç
ðÿäà ïî÷òè ðàâíîñòîÿùèõ â øêàëå ÷àñòîò ëèíèé, èíòåíñèâíîñòü êîòîðûõ áûñòðî
óáûâàåò ñ ÷àñòîòîé.
Ìû êàê áû èìååì îñíîâíîé òîí è ðÿä ãàðìîíèê, ïðèñóòñòâèå ïîñëåäíèõ
îáúÿñíÿåòñÿ àíãàðìîíè÷íîñòüþ ìîëåêóëû - îñöèëëÿòîðà.
Äåéñòâèòåëüíî, ïîòåíöèàëüíàÿ êðèâàÿ ìîëåêóëû, îïèñûâàþùåé
4
Ëàáîðàòîðíàÿ ðàáîòà ¹72
çàâèñèìîñòü îò
-1
E(ñì )
ìåæàòîìíîãî ðàññòîÿíèÿ
(ðèñ. 3) òîëüêî â ñâîåé
4000
íèæíåé ÷àñòè èìååò
ôîðìó ïàðàáîëû âòîðîãî
ïîðÿäêà. Ñ óâåëè÷åíèåì
3000
ðàññòîÿíèÿ
ìåæäó
àòîìàìè, ñèëà èõ
2000
âçàèìíîãî ïðèòÿæåíèÿ
ñòðåìèòñÿ ê íóëþ (ïî
1000
ýêñïîíåíòå
äëÿ
r (10-8ñ
ãîìåîïîëÿðíûõ
4,0
1,0 rl 2,0
3,0
ìîëåêóë), à ýíåðãèÿ - ê
ïîñòîÿííîé âåëè÷èíå
Ðèñ.3.
ýíåðãèè äèññîöèàöèè
ìîëåêóëû; íàîáîðîò, ñáëèæåíèå àòîìîâ äîëæíî ñîïðîâîæäàòüñÿ áûñòðûì
ðîñòîì ñèëû îòòàëêèâàíèÿ èõ ÿäåð.
Ó÷åò àíãàðìîíè÷íîñòè ïðèâîäèò ê ïîÿâëåíèþ â âûðàæåíèè (4) äîáàâî÷íûõ
3
2
÷ëåíîâ. Òåïåðü:
(5)
E ê î ë = h c w ( u + 12 ) - h c w x ( u + 12 ) + h c w y ( u + 12 )
Çäåñü ìû ïîëüçóåìñÿ íåñêîëüêî ãðîìîçäêèìè, îáùåïðèíÿòûìè
îáîçíà÷åíèÿìè. Åñëè àíãàðìîíè÷íîñòü ìàëà, òî ω >> ωx >> ωy
Óðîâíè ýíåðãèè àíãàðìîíè÷åñêîãî îñöèëëÿòîðà íå ÿâëÿþòñÿ
ðàâíîñòîÿùèìè, ðàññòîÿíèå ìåæäó íèìè óáûâàåò ñ ðîñòîì ÷èñëà υ . Óñëîâèå
∆υ = ±1 äîïîëíÿåòñÿ óñëîâèåì ∆υ = ±2, ±3,K (6) Îäíàêî, âåðîÿòíîñòü òàêèõ
ïåðåõîäîâ áûñòðî óáûâàåò ñ ðîñòîì ∆υ , ýòèì îáúÿñíÿåòñÿ íàáëþäàåìàÿ â
äåéñòâèòåëüíîñòè ìàëàÿ èíòåíñèâíîñòü ãàðìîíèê ïî ñðàâíåíèþ ñ îñíîâíûì
òîíîì. Îáåðòîíû, ñîãëàñíî (5) ,(6) , íå êðàòíû îñíîâíîé ÷àñòîòå, ÷àñòîòà èõ
íåñêîëüêî ìåíüøå. Òàê êàê óâåëè÷åíèå ðàññòîÿíèÿ ìåæäó
àòîìàìè ñîïðîâîæäàåòñÿ áîëåå ìåäëåííûì ðîñòîì ñèëû ïðèòÿæåíèÿ, ÷åì ðîñò
ñèëû îòòàëêèâàíèÿ ïðè èõ ñáëèæåíèè (ñì. ðèñ.3), ñðåäíåå ïî âðåìåíè
ìåæàòîìíîå ðàññòîÿíèå ïðè íàëè÷èè êîëåáàíèÿ áóäåò áîëüøå ðàâíîâåñíîãî
(r0 ), ïîýòîìó ìîìåíò èíåðöèè, à ñëåäîâàòåëüíî è êîíñòàíòà B äîëæíû çàâèñåòü îò
êîëåáàòåëüíîãî ñîñòîÿíèÿ ìîëåêóë.
Ñîãëàñíî êâàíòîâîé ìåõàíèêå, â ïåðâîì ïðèáëèæåíèè
B u = B e - a ( u + 12 )
Be - ñîîòâåòñòâóåò íåîñóùåñòâèìîìó ñîñòîÿíèþ, êîãäà êîëåáàíèÿ
îòñóòñòâóþò. Êîíñòàíòà α << Be . Âðàùàòåëüíàÿ ïîñòîÿííàÿ B0 , îïðåäåëÿåìàÿ
èç ÷èñòî âðàùàòåëüíûõ ñïåêòðîâ (äàëåêàÿ èíôðàêðàñíàÿ îáëàñòü) , ñîîòâåòñòâóåò
íàèíèçøåìó êîëåáàòåëüíîìó ñîñòîÿíèþ, êîãäà υ = 0 , òàê êàê ïðè îáû÷íîé
(êîìíàòíîé) òåìïåðàòóðå êîëåáàòåëüíûå óðîâíè ïî÷òè íå âîçáóæäàþòñÿ.
5
Ëàáîðàòîðíàÿ ðàáîòà ¹72
Êîëåáàòåëüíî-âðàùàòåëüíûå ñïåêòðû.
Ðàññìàòðèâàÿ êîëåáàòåëüíîå äâèæåíèå ìîëåêóëû, ìû íå ó÷èòûâàåì åå
âðàùåíèÿ. Òàê êàê îáà äâèæåíèÿ ñóùåñòâóþò îäíîâðåìåííî, ñîãëàñíî ôîðìóëàì
(1) è (5) äëÿ âðàùàòåëüíî-êîëåáàòåëüíîé ýíåðãèè ìîëåêóëû Eâê èìååì:
E âê = w h c
[( u +
1
2
) - x ( u + 12 ) 2 + K ] +
B u h c j( j + 1 )
n ñ ì - 1 = n ê î ë + B ¢u j¢ ( j¢ + 1) - B ¢¢u j¢¢ ( j¢¢ + 1 )
(7)
(8)
ãäå νêîë ñîîòâåòñòâóåò ÷èñòî êîëåáàòåëüíîìó ïåðåõîäó, ïðè îòñóòñòâèè
âðàùåíèÿ.
Ñîâîêóïíîñòü ëèíèé, îïèñûâàåìûõ ôîðìóëîé (8), ïðè íåèçìåííîé
νêîë îáðàçóåò ïîëîñó. Ëèíèè, äëÿ êîòîðûõ j ′′ − j ′ = −1 ïðèíàäëåæàò, òàê
íàçûâàåìîé, âåòâè R, à ëèíèè äëÿ êîòîðûõ j ′′ − j ′ = 1 , îáðàçóþò P âåòâü. Åñëè
íå ó÷èòûâàòü çàâèñèìîñòü êîíñòàíòû Bυ îò êîëåáàòåëüíîãî êâàíòîâîãî ÷èñëà,
ïîëó÷èì äëÿ R âåòâè:
(9)
ν = νêîë + 2 Bj ′; j ′ = 1, 2, 3, K
à äëÿ P âåòâè:
(10)
n = n ê î ë - 2 B ( j¢ + 1 ) ; j¢ = 0 ,1, 2 , K
Èç ôîðìóë (9) è (10) ñëåäóåò, ÷òî ðàññòîÿíèå ìåæäó ñîñåäíèìè ëèíèÿìè â
îáåèõ âåòâÿõ îäèíàêîâû è ðàâíû 2B , ìåæäó âåòâÿìè èìåþòñÿ ïðîìåæóòêè,
ðàâíûå 4B . Íà ðèñ.2 ïîêàçàíà íàáëþäàåìàÿ ýêñïåðèìåíòàëüíî òîíêàÿ
ñòðóêòóðà â ïîëîñå ïîãëîùåíèÿ ìîëåêóëû HCl . Òàê êàê äîñòèæèìàÿ íà
ïðàêòèêå ðàçðåøàþùàÿ ñèëà ïðèáîðîâ â èíôðàêðàñíîé îáëàñòè íåâåëèêà,
îáíàðóæèòü òîíêóþ ñòðóêòóðó âðàùàòåëüíî-êîëåáàòåëüíûõ ñïåêòðîâ óäàåòñÿ
òîëüêî ó ëåãêèõ ìîëåêóë, èìåþùèõ ìàëûé ìîìåíò èíåðöèè è ñëåäîâàòåëüíî
øèðîêî ðàññòàâëåííûå ëèíèè. Èçìåðÿÿ ðàññòîÿíèÿ ìåæäó ñîñåäíèìè ëèíèÿìè,
ìîæíî îïðåäåëèòü êîíñòàíòó B , à ñëåäîâàòåëüíî ìîìåíò èíåðöèè è ìåæàòîìíîå
ðàññòîÿíèå â ìîëåêóëå.
Ýëåêòðîííûå óðîâíè ìîëåêóëû.
Ïðè îáúåäèíåíèè àòîìîâ â ìîëåêóëó èõ âíåøíèå ýëåêòðîíû â òîé èëè
èíîé ñòåïåíè (ýòî çàâèñèò îò âèäà ñâÿçè) òåðÿþò èíäèâèäóàëüíóþ ïðèíàäëåæíîñòü
ê îïðåäåëåííîìó àòîìó è îáðàçóåò ýëåêòðîííóþ îáîëî÷êó ìîëåêóëû.
Ýíåðãåòè÷åñêèå óðîâíè ýòîé îáîëî÷êè ìîæíî ðàññìàòðèâàòü, êàê ðåçóëüòàò
øòàðêîâñêîãî ðàñùåïëåíèÿ ñîîòâåòñòâóþùèõ óðîâíåé àòîìîâ â ýëåêòðè÷åñêîì
ïîëå ìîëåêóëû. (Ïîëå ñîçäàâàåìîå ÿäðàìè è ýêðàíèðóþùèìè èõ âíóòðåííèìè
ýëåêòðîííûìè îáîëî÷êàìè). Ýòî ïîëå â íàøåì ñëó÷àå, î÷åâèäíî, èìååò îñåâóþ
ñèììåòðèþ. Âñëåäñòâèå âðàùåíèÿ ýëåêòðîíîâ, ýëåêòðîííàÿ îáîëî÷êà ìîëåêóëû
îáëàäàåò ìîìåíòîì êîëè÷åñòâà äâèæåíèÿ L , âåëè÷èíà êîòîðîãî, ñîãëàñíî
êâàíòîâîé ìåõàíèêå, â åäèíèöàõ h 2π ïðèíèìàåò öåëî÷èñëåííûå çíà÷åíèÿ.
 ýëåêòðè÷åñêîì ïîëå ìîëåêóë, âåêòîð L ìîæåò îðèåíòèðîâàòüñÿ
( 2 L + 1 ) ðàçëè÷íûìè ñïîñîáàìè, òàê ÷òî åãî ïðîåêöèÿ íà îñü ìîëåêóëû
L = ± L ,± ( L - 1 ) , K , 0 . Ñîñòîÿíèÿ, îòëè÷àþùååñÿ çíàêîì Λ , åñëè íå
6
Ëàáîðàòîðíàÿ ðàáîòà ¹72
ó÷èòûâàòü âçàèìîäåéñòâèÿ ñ âðàùåíèåì ìîëåêóëû (ýòîò ó÷åò ïðèâåäåò ê ìàëîìó,
çàâèñÿùåìó îò j ðàñùåïëåíèþ óðîâíåé, äëÿ êîòîðûõ Λ = 0 ), ýíåðãåòè÷åñêè
ýêâèâàëåíòíû, ïîýòîìó äëÿ êàæäîãî Λ èìååòñÿ L + 1 ýíåðãåòè÷åñêè ðàçëè÷íûõ
ñîñòîÿíèé. Òàê êàê L öåëîå ÷èñëî, òî Λ ìîæåò ïðèíèìàòü òîæå òîëüêî öåëûå
çíà÷åíèÿ.
Ñïèíû îòäåëüíûõ ýëåêòðîíîâ, îðèåíòèðóÿñü ïàðàëëåëüíî íåêîòîðîìó
îáùåìó íàïðàâëåíèþ, îáðàçóþò ðåçóëüòèðóþùèé ñïèí S = ΣSi , ãäå Si = ± 12 â
åäèíèöàõ h 2π .
Âåëè÷èíà 2S îïðåäåëÿåò ÷èñëî íåêîìïåíñèðîâàííûõ ñïèíîâ è ðàâíà
âàëåíòíîñòè ìîëåêóëû. Âíóòðåííèå ýëåêòðîíû ìîëåêóëû îáðàçóþò çàìêíóòûå
îáîëî÷êè, äëÿ êîòîðûõ L è S ðàâíû 0. Âñëåäñòâèå ïðåöåñèè âåêòîðà L â
ýëåêòðè÷åñêîì ïîëå ìîëåêóëû, ñðåäíåå ïî âðåìåíè ìàãíèòíîå ïîëå,
îáóñëîâëåííîå îðáèòàëüíûì äâèæåíèåì ýëåêòðîíîâ îáîëî÷êè, ïàðàëëåëüíî
îñè ìîëåêóëû, ïîýòîìó ýíåðãèÿ ìàãíèòíîãî âçàèìîäåéñòâèÿ ñïèíà ñ
îðáèòàëüíûì äâèæåíèåì çàâèñèò òîëüêî îò âåëè÷èíû ïðîåêöèè ñïèíà ε íà ýòó
îñü
e = ± S ,± ( S - 1 ) , K .0
Ýòî âçàèìîäåéñòâèå ïðèâîäèò, êàê â àòîìå, ê ðàñùåïëåíèþ ýëåêòðîííûõ
ýíåðãåòè÷åñêèõ óðîâíåé íà 2 S + 1 ïîäóðîâíåé.
Ïðè ñèëüíîì âçàèìîäåéñòâèè îðáèòàëüíîãî è ñïèíîâîãî ìîìåíòîâ (ñëó÷àé
r
"à" ïî Ãóíäó) ïðîåêöèè âåêòîðîâ Lr è S íà ìîëåêóëÿðíóþ îñü äàþò
r
r
ðåçóëüòèðóþùèå ìîìåíòû W , W = L + re êîòîðûå ñêëàäûâàÿñü ñ âðàùàòåëüíûì
r
ìîìåíòîì êîëè÷åñòâà äâèæåíèÿ N , îáðàçóþò ïîëíûé ìîìåíò êîëè÷åñòâà
r
äâèæåíèÿ ìîëåêóëû y . Âåëè÷èíà ïîñëåäíåãî îïðåäåëÿåòñÿ êâàíòîâûì ÷èñëîì
J , êîòîðîå ìîæåò ïðèíèìàòü òîëüêî öåëûå èëè ïîëóöåëûå çíà÷åíèÿ
r
y=
J ( J + 1) , J = W , W + 1, W + 2, K
Ñëó÷àé (à) èìååò ìåñòî îáû÷íî äëÿ òÿæåëûõ ìîëåêóë. Èñêëþ÷åíèÿ
ïðåäñòàâëÿþò ε - óðîâíè äëÿ êîòîðûõ îòñóòñòâóåò ñâÿçü ìåæäó L è S .
r
r
 ñëó÷àå (â), õàðàêòåðíîì äëÿ ëåãêèõ ìîëåêóë, Λ è S îáû÷íî ñëàáåå ñâÿçè
r
r
r
Λ è N , êîòîðûå râ ñóììå äàþò âåêòîð k , ïîñëåäíèé âìåñòå ñî ñïèíîì îáðàçóþò
ïîëíûé ìîìåíò J .
Ñëó÷àé (ñ) ñîîòâåòñòâóåò Øòàðê-ýôôåêòó â ñëàáîì ïîëå, êîãäà ñâÿçü ìåæäó
r
r
r
r
r
è
íå
íàðóøàåòñÿ
ïîëåì.
Âåêòîðà
è
îáðàçóþò
ñíà÷àëà
âåêòîð
,
J
L
L
S
S
n
r
ïðîåêöèÿ êîòîðîãî Ω íà îñü ìîëåêóëû âìåñòå ñ âåêòîðîì N îáðàçóþò ïîëíûé
r
ìîìåíò ìîëåêóëû J .
×èñëà Λ è ε äëÿ ñëó÷àÿ (â) è (ñ) íå èìååò ñìûñëà. Ïåðåõîä îò ñëó÷àåâ (à) è
(â) ê ñëó÷àþ (ñ) äîëæåí , î÷åâèäíî, èìåòü ìåñòî ïðè ðàçäâèæåíèè ÿäåð.
 ñëó÷àå (à) òåðìû çàïèñûâàþòñÿ àíàëîãè÷íî àòîìíûì, ñîñòîÿíèÿ äëÿ
êîòîðûõ Λ = 0 , 1, 2, 3 îáîçíà÷àþòñÿ ãðå÷åñêèìè áóêâàìè Σ , π , ∆ , Φ ñîîòâåòñòâåííî, â âåðõíåì ëåâîìó óãëó áóêâû îòìå÷àåòñÿ ìóëüòèïëåòíîñòü, îíà
7
Ëàáîðàòîðíàÿ ðàáîòà ¹72
ðàâíà 2 S + 1, â ïðàâîì íèæíåì çàïèñûâàåòñÿ âåëè÷èíà Ω . Íàïðèìåð, 2 π
îçíà÷àåò, ÷òî â ýòîì ñîñòîÿíèè Λ = 1, S = 12 , Ω = 32 .  ñëó÷àå (â) òåðì
3
2
çàïèñûâàåòñÿ òàê: 2 S + 1{ L } ; â ñëó÷àå (ñ) çàïèñûâàåòñÿ òîëüêî Ω .
Ýëåêòðîííî-êîëåáàòåëüíûå ñïåêòðû.
 êàæäîì óñòîé÷èâîì ýëåêòðîííîì ñîñòîÿíèè ïîòåíöèàëüíàÿ êðèâàÿ
ìîëåêóëû èìååò ìèíèìóì, òàêàÿ ìîëåêóëà ìîæåò ñîâåðøàòü êîëåáàòåëüíî è
âðàùàòåëüíîå äâèæåíèå. Ïîëíàÿ ýíåðãèÿ ìîëåêóëû áóäåò ðàâíà ñóììå ýíåðãèè
- ýëåêòðîííîé E ýë , êîëåáàòåëüíîé E êîë , âðàùàòåëüíîé Eâð : E = E ýë + Eêîë + Eâð
(11) Ïåðåõîäû ìåæäó äâóìÿ ðàçëè÷íûìè ýíåðãåòè÷åñêèìè ñîñòîÿíèÿìè áóäóò
ñîïðîâîæäàòüñÿ èçëó÷åíèåì ÷àñòîòû
ν=
1
′ ) + (E′âð − E′âð′ )]
[(E′ýë − E′ýë′ ) + (E′êîë − E′êîë
hÑ
(12)
Òàê êàê ðàññòîÿíèå ìåæäó ýëåêòðîííûìè óðîâíÿìè, êàê ïðàâèëî,
îòíîñèòåëüíî âåëèêî, ýëåêòðîííî-êîëåáàòåëüíûé ñïåêòð ìîëåêóëû ðàñïîëîæåí
â âèäèìîé èëè óëüòðàôèîëåòîâîé îáëàñòè . êâàíòîâàÿ ìåõàíèêà ñèëüíî
îãðàíè÷èâàåò ÷èñëî âîçìîæíûõ êîìáèíàöèé ìåæäó òåðìàìè ïðàâèëàìè îòáîðà.
Òîíêàÿ ñòðóêòóðà ýëåêòðîííî-êîëåáàòåëüíîãî ñïåêòðà.
Äëÿ âðàùàòåëüíîé ýíåðãèè ìîëåêóëû Eâð ñ ó÷åòîì ýíåðãèè äâèæåíèÿ
j'
9
8
7
6
5
4
3
21
0
R
j
P
9 8 7 6 5 4 3 2 10
m
1 2 3 4 5 6 7 8 910
109 8 7 6 5 4 3 2 1 -1-2 -3 -4 -5 -6 -7-8 -9 -10
8
ν0
Ðèñ.4.
λ
9
8
7
6
5
4
3
21
0
ν0
Ðèñ.5.
P(5)
10
R(3)
R(2)
R(1)
R(0)
Q(1)
Q(7)
P(2)
P(3)
P(4)
P(5)
j''
j'
R(3)
R(2)
R(1)
R(0)
Q(1)
Q(7)
P(2)
P(3)
R(9)
R(8)
R(7)
R(6)
R(5)
R(4)
R(3)
R(2)
R(1)
R(0)
P(1)
P(2)
P(3)
P(4)
P(5)
P(6)
P(7)
P(8)
P(9)
P(10)
10
λ
8
7
6
5
4
3
12
j''
9
8
7
6
5
4
23
01
Ëàáîðàòîðíàÿ ðàáîòà ¹72
ýëåêòðîíîâ â ñëó÷àå ñâÿçè (à), êâàíòîâàÿ ìåõàíèêà äàåò ñëåäóþùåå âûðàæåíèå:
E âð = hCB{j(j + 1) − Ω 2 }
(13)
 ε ñîñòîÿíèå Ω = 0 è ìû ïðèõîäèì ê ïðàâèëüíîìó âûðàæåíèþ (1). Íèæíèå
ýíåðãåòè÷åñêèå óðîâíè áîëüøèíñòâà ìîëåêóë ÿâëÿþòñÿ ε óðîâíÿìè.
Îáîçíà÷àÿ ÷åðåç ν ýê ÷àñòîòó, êîòîðàÿ ñîîòâåòñòâóåò ïåðåõîäó ïðè îòñóòñòâèè
âðàùåíèÿ, íà îñè (12) è (13) ïîëó÷èì:
(14)
ν = ν ýê + B′{j′(j′ + 1) − Ω′2 }− B′′{j′′(j′′ + 1) − Ω′′2 }
Òåïåðü B′ è B′′ îòíîñÿòñÿ ê ðàçëè÷íûì ýëåêòðîííûì óðîâíÿì.
Êàê óêàçûâàëîñü âûøå, j ìîæåò ìåíÿòüñÿ íà ± 1 èëè îñòàåòñÿ áåç èçìåíåíèÿ.
Ñîîòâåòñòâåííî ýòèì òðåì âîçìîæíîñòÿì áóäåì èìåòü ñåðèè ëèíèé èëè òðè
âåòâè:
P âåòâü:
(15)
j′′ = j′ + 1 , ν = ν 0 + (B′ − B′′)j′2 − (3 B′′ − B′)j′ − 2B′′
Q âåòâü:
j′′ = j′ , ν = ν 0 + (B′ − B′′)j′(j′ + 1)
(16)
R âåòâü:
j′′ = j′ − 1 , ν = ν 0 + (B′ − B′′)j′2 + (B′ + B′′)j′
(17)
Íåçàâèñÿùèå îò j ÷ëåíà ìû âêëþ÷èì â êîíñòàíòó ν 0 . Ôîðìóëû (15) è (17)
ìîæíî îáúåäèíèòü â îäíó:
ν = ν 0 + (B′ + B′′)m + (B′ − B′′)m 2
(18)
ãäå m = − (j′ + 1) äëÿ P ïîëîñû, m = j′ äëÿ R ïîëîñû.
Íà ðèñ.5 ïîêàçàíà ñõåìà ïåðåõîäîâ ìåæäó 1 π (Λ′ = 1) è 1 Σ(Λ ′ = 0 ) ñîñòñÿíèÿìè,
ïðèâîäÿùèõ ê îáðàçîâàíèþ P, Q, R âåòâåé. Òàê êàê j′ = Ω′, Ω′ + 1, Ω′ + 2,K
íàèìåíüøåå çíà÷åíèå j′ = 1 , ïîýòîìó â P âåòâè ëèíèÿ ν = ν 0 − 2B′′ , à â ïîëîñå Q
- ëèíèÿ ν = ν 0 (íóëåâàÿ ëèíèÿ ) îòñóòñòâóåò.
Ðàññìàòðèâàÿ ν , êàê íåïðåðûâíóþ ôóíêöèþ j, ñîãëàñíî (15), (16), (17)
ïîëó÷èì ó÷àñòêè òðåõ ïàðàáîë - ïàðàáîëû Ôîðòðàòà.
Íà ðèñ.6à ïîêàçàíû òàêèå ïàðàáîëû, ïîñòðîåííûå äëÿ ïîëîñû
|m|
25
20
Q
R
15
10
5
23600
R
Ñïåêòð
23500
23400
23300
Ðèñ.6à.
2
9
Ëàáîðàòîðíàÿ ðàáîòà ¹72
20
P
15
10
20
Q
5 43
15
1
R
-1
23008ñì
Ðèñ.6á.
o
λ = 4241 A ìîëåêóëû AlH, âíèçó èçîáðàæåíà ñàìà ïîëîñà (ðèñ 6á)
Âîçíèêíîâåíèå êàíòà ñâÿçàíî ñ êâàäðàòè÷íûì ÷ëåíîì â ôîðìóëàõ (15) è
(17). Êàêàÿ èç âåòâåé åãî îáðàçóåò, çàâèñèò îò çíàêà ðàâåíñòâà (B′ − B′′ ) . Åñëè
B′ > B′′ , êàíò îáðàçóåòñÿ âåòâüþ P, åñëè æå B′ < B′′ - âåòâüþ R. Òàêèì îáðàçîì,
ïî õàðàêòåðó îòòåíåíèÿ ìîæíî ñóäèòü óâåëè÷èâàåòñÿ èëè óìåíüøàåòñÿ
ìåæàòîìíîå ðàññòîÿíèå ïðè âîçáóæäåíèè ýëåêòðîííîãî óðîâíÿ. Åñëè êîíñòàíòà
B′e è B′e′ áëèçêè ïî âåëè÷èíå, ñ ðîñòîì êîëåáàòåëüíîãî ÷èñëà (υ) ðàçíîñòü
B′υ − B′υ′ ìîæåò èçìåíÿòü çíàê, ÷òî äîëæíî ñîïðîâîæäàòüñÿ èçìåíåíèåì õàðàêòåðà
îòíîøåíèé. Òàêîå ÿâëåíèå èìååò ìåñòî äëÿ ôèîëåòîâîé ñèñòåìû ïîëîñ öèàíà,
ôèîëåòîâîå îòòåíåíèå èíòåíñèâíûõ ïîëîñ äèàãîíàëüíîé ãðóïïû (υ′ = υ′′) ,
ñîîòâåòñòâóþùèõ ìàëûì υ , ñìåíÿåòñÿ êðàñíûì ïðè áîëüøèõ υ ýòî ñëàáûå,
ò.í. "’õâîñòîâûå ïîëîñû".
Îïðåäåëåíèå âðàùàòåëüíûõ ïîñòîÿííûõ.
Ðàçíîñòü ÷àñòîò äâóõ ëèíèé, îäíà èç êîòîðûõ ïðèíàäëåæèò R, à âòîðàÿ P
âåòâÿì ïîëîñû, è îáå èìåþò îáùèé âåðõíèé âðàùàòåëüíûé óðîâåíü (ñì ðèñ
4), çàâèñèò òîëüêî îò êîíñòàíòû B′ è íå çàâèñèò îò êîíñòàíòû B′′ . Àíàëîãè÷íàÿ
ðàçíîñòü, ñîîòâåòñòâóþùàÿ äâóì ïåðåõîäàì íà îáùèé íèæíèé âðàùàòåëüíûé
óðîâåíü åñòü ôóíêöèÿ B′ è íå çàâèñèò îò B′′ . Îáîçíà÷àÿ ïåðâóþ ðàçíîñòü ÷åðåç
∆ν′ , à âòîðóþ ÷åðåç ∆ν′′ íà îñíîâå ôîðìóëû (14) íàéäåì , ÷òî:
∆ν′′ = B′′(j′′ + 1)(j′′ + 2 ) − B′′(j′′ − 1)j′′ = 4 B′′(j′′ + 12 )
(19)
∆ν′ = B′(j′ + 1)(j′ + 2 ) − B′(j′ − 1)j′ = 4 B′(j′ + 21 )
(20)
ãäå j′ è j′′ îòíîñÿòñÿ ê îáùåìó äëÿ äàííîé ïàðû ïåðåõîäîâ âðàùàòåëüíîìó
óðîâíþ.
ÝÊÑÏÅÐÈÌÅÍÒÀËÜÍÀß ×ÀÑÒÜ.
Çàäà÷à íàñòîÿùåé ðàáîòû ÿâëÿåòñÿ îïðåäåëåíèå ìîìåíòà èíåðöèè ìîëåêóëû
öèàíà ïî åãî ýëåêòðîííîé ïîëîñå.
Äëÿ âûïîëíåíèÿ ðàáîòû íåîáõîäèìî ñíÿòü ñïåêòð óãîëüíîé äóãè è, èçìåðèâ
ïîëó÷åííóþ ñïåêòðîãðàììó íà êîìïàðàòîðå, îïðåäåëèòü âîëíîâûå ÷èñëà ëèíèé
10
Ëàáîðàòîðíàÿ ðàáîòà ¹72
o
ïîëîñû ñ êàíòîì 3883 A .
Äàëåå íåîáõîäèìî îïðåäåëèòü âðàùàòåëüíûå êâàíòîâûå ÷èñëà P è R âåòâåé
äàííîé ïîëîñû, èñïîëüçóÿ ïðè ýòîì ñõåìó èõ îáðàçîâàíèÿ è ñðàâíèâàÿ
ïîëó÷åííûé ñïåêòð ñî ñïåêòðîì, èçîáðàæåííûì íà ðèñ. 6á. Çàòåì ïî ôîðìóëàì
(19) è (20) íàõîäÿòñÿ âðàùàòåëüíûå ïîñòîÿííûå B′ è B′′ äëÿ âåðõíåãî è íèæíåãî
ýíåðãåòè÷åñêèõ ñîñòîÿíèé. Ìîìåíò èíåðöèè ìîëåêóëû öèàíà âû÷èñëÿåòñÿ ïî
ôîðìóëå (2) äëÿ îáîèõ ýíåðãåòè÷åñêèõ ñîñòîÿíèé.
Ñïåêòðîãðàììà ñíèìàåòñÿ íà ñïåêòðîãðàôå ÄÔÑ-8, ïðèíöèïèàëüíàÿ ñõåìà
5
3
4
2
1
Ðèñ.7.
êîòîðîãî äàíà íà ðèñ.7 (Ýìèññèîííûé ñïåêòðàëüíûé àíàëèç àòîìíûõ
ìàòåðèàëîâ, ñòð. 670 , ðèñ. V)
Êàê âèäíî èç ðèñ.7, ýòî àâòîêîëëèìàöèîííûé ñïåêòðîãðàô ñ
ïîëîñêîé äèôðàêöèîííîé ðåøåòêîé. Â íàøåì ïðèáîðå ñòîèò ðåøåòêà 600
o
øòðèõîâ íà ìì, êîòîðàÿ â ïåðâîì ïîðÿäêå èìååò äèñïåðñèþ 6 A /ìì. Òàêàÿ
äèñïåðñèÿ ìàëà äëÿ õîðîøåãî ðàçðåøåíèÿ ñòðóêòóðû ïîëîñû. Ïîýòîìó ñïåêòð
íàäî ñíèìàòü âî âòîðîì ïîðÿäêå.
Äëÿ óñïåøíîãî âûïîëíåíèÿ ðàáîòû íàäî ïîëó÷èòü ñíèìîê î÷åíü
õîðîøåãî êà÷åñòâà è áåç ôîíà. Ýòî âîçìîæíî ïðè íåïðåìåííîì ñîáëþäåíèè
ñëåäóþùèõ óñëîâèé:
à) õîðîøàÿ ôîêóñèðîâêà ñïåêòðîãðàôà è ïðàâèëüíî âûáðàííàÿ øèðèíà
ùåëè;
á) ïðàâèëüíîå îñâåùåíèå ùåëè,
â) òùàòåëüíî îòðàáîòàííàÿ ñïåêòðîãðàììà.
Ñïåêòðîãðàô
óæå
ñôîêóñèðîâàí; ïåðåä íà÷àëîì
ðàáîòû íåîáõîäèìî òîëüêî
ïðîâåðèòü íå ñáèëàñü ëè
ôîêóñèðîâêà. Äàííûå
14
15
ôîêóñèðîâêè ñïåêòðîãðàôà
ñìîòðèòå â îïèñàíèè ïðèáîðà,
êîòîðîå íàõîäèòüñÿ
íà
óñòàíîâêå.
Øèðèíà ùåëè óñèëèâàåòñÿ ïî
ñîîòâåòñòâóþùåìó áàðàáàí÷èêó,
öåíà äåëåíèÿ êîòîðîãî ðàâíà 1
Ðèñ.8.
11
Ëàáîðàòîðíàÿ ðàáîòà ¹72
ìèêðîíó. Ñâåòîñèëà ñïåêòðîãðàôà ðàâíà 1:35. Íåîáõîäèìî îïðåäåëèòü
îïòèìàëüíóþ øèðèíó ùåëè äëÿ òîé îáëàñòè äëèí âîëí, â êîòîðîé
áóäåò ñíèìàòüñÿ ñïåêòð.
Äëÿ ïîëíîãî èñïîëüçîâàíèÿ ñâåòîñèëû ïðèáîðà è ðàâíîìåðíîãî
îñâåùåíèÿ ùåëè, ïðèíèìàåòñÿ àõðîìàòè÷åñêàÿ òðåõëèíçîâàÿ îñâåòèòåëüíàÿ
ñèñòåìà (ðèñ.9). Îòñ÷åò ðàññòîÿíèÿ ïðîèçâîäèòñÿ îò ñåðåäèíû îïðàâ
êîíäåíñàòîðîâ.
3 298ìì 5
2
1
594ìì
6
4
692ìì
1 - èñòî÷íèê ñâåòà,
2,3,4 - êîíäåíñîðû
5 - ùåëü,
6 - êîëëèìàòîðíûé îáúåêòèâ.
Îòñ÷åò ðàññòîÿíèÿ ïðîèçâîäèòñÿ îò ñåðåäèíû îïðàâ êîíäåíñîðîâ.
Ðèñ.9.
Èñòî÷íèê ñâåòà (1) ïðîåêòèðóåòñÿ êîíäåñàòîðîì (2) - ôîêóñíîå ðàññòîÿíèå
75 ìì, íà ïëîñêîñòü ãëàâíîãî ñå÷åíèÿ êîíäåñàòîðà (3) f = 150 ìì. Ïîñëåäíèé
ïðîåêòèðóåò óìåíüøåííîå èçîáðàæåíèå êîíäåíñàòîðà (2) íà ïëîñêîñòü ùåëè
ñïåêòðîãðàôà (5) è, íàêîíåö, ëèíçà (4) - f = 320 ìì, óñòàíîâëåííàÿ
íåïîñðåäñòâåííî ïåðåä ùåëüþ ñïåêòðîãðàôà, ôîêóñèðóåò ëèíçó (3) íà ãëàâíóþ
ïëîñêîñòü êîëëèìàòîðíîãî îáúåêòèâà (6), â íàøåì ñëó÷àå ýòî ñôåðè÷åñêîå
çåðêàëî. Î÷åâèäíî, äëÿ òîãî, ÷òîáû êîëëèìàòîðíûé îáúåêòèâ áûë çàïîëíåí
ñâåòîì, èçîáðàæåíèå èñòî÷íèêà èëè âûäåëåííîé åãî ÷àñòè äîëæíî áûòü íå
ìåíåå ðàçìåðîâ îáúåêòèâà. Èç ýòîãî óñëîâèÿ ðàññ÷èòûâàåòñÿ óâåëè÷åíèå âñåé
îñâåòèòåëüíîé ñèñòåìû. Ïðèáëèæåííûé ðàñ÷åò òðåõëèíçîâîé ñèñòåìû äîâîëüíî
ïðîñò, íà íåì ìû íå îñòàíàâëèâàåìñÿ, òàê êàê ê ñïåêòðîãðàôàì îáû÷íî
ïðèëàãàåòñÿ ðàññ÷èòàííûå è èçãîòîâëåííûå çàâîäîì îñâåòèòåëüíûå ñèñòåìû.
Òàêîãî ðîäà ñèñòåìû îáåñïå÷èâàþò îñâåùåíèå êàæäîé òî÷êè ùåëè
âñåìè òî÷êàìè èñòî÷íèêà ñâåòà, òî÷íåå òîãî åãî ó÷àñòêà, êîòîðûé âûäåëåí
ïðîìåæóòî÷íîé äèàôðàãìîé. Ïîýòîìó ùåëü îñâåùåíà ðàâíîìåðíî, íåçàâèñèìî
îò ðàñïðåäåëåíèÿ ÿðêîñòè â èñòî÷íèêå. Ïîòîê ñâåòà îò êàæäîãî ýëåìåíòà
ùåëè, äîñòèãàþùèé ïðèåìíèêà ñâåòà, ïðîïîðöèîíàëåí îñâåùåííîñòè ùåëè, è
îñâåùåííîñòü èçîáðàæåíèÿ ùåëè â ôîêàëüíîé ïëîñêîñòè ïðèáîðà òàêæå
ðàâíîìåðíà. Ïðîìåæóòî÷íàÿ äèàôðàãìà ïîçâîëÿåò âûäåëèòü ñâåò òîëüêî îò
÷àñòè èñòî÷íèêà èëè óñòðàíèòü ñâåò, ìåøàþùèé àíàëèçó (íàïðèìåð, ñâåò îò
ðàñêàëåííûõ ýëåêòðîäîâ, óâåëè÷èâàþùèé ñïëîøíîé ôîí).
12
Ëàáîðàòîðíàÿ ðàáîòà ¹72
Ïîäðîáíûé ðàñ÷åò òðåõëèíçîâîé ñèñòåìû ñì. â êíèãå Â Ê Ïðîêîôüåâà , Ì
-Ë ,1951ã. "Ôîòîãðàôè÷åñêèå ìåòîäû êîëè÷åñòâåííîãî ñïåêòðàëüíîãî àíàëèçà
ìåòàëëîâ è ñïëàâîâ", ò.1, §18 , ñïîñîá 7 (ñòð. 156)
Äëÿ îïðåäåëåíèÿ âîëíîâûõ ÷èñåë ïîëîñû ÑN ïîëüçóþòñÿ ñïåêòðîì æåëåçà,
ïîýòîìó âñòûê ñî ñïåêòðîì ÑN íåîáõîäèìî
S
S
ñíÿòü ñïåêòð æåëåçà. Äëÿ ýòîãî ïåðåä ùåëüþ
0 2 4 6 8 10
ñïåêòðîãðàôà óñòàíàâëèâàåòñÿ ñïåöèàëüíàÿ
I
II
äèàôðàãìà "ëàñòî÷êèí õâîñò", ðèñ.10.
Êîãäà äèàôðàãìà ñòîèò ïî îòíîøåíèþ ê
0 2 4 6 8 10
ùåëè S â ïîëîæåíèè 1, îòêðûòà ñðåäíÿÿ
÷àñòü ùåëè - ïðè òàêîì ïîëîæåíèè äèàôðàãìû
Ðèñ.10.
íàäî ñíÿòü ñïåêòð ÑN. Åñëè äèàôðàãìà
ïîñòàâëåíà â ïîëîæåíèå 2 - ñðåäíÿÿ ÷àñòü
ùåëè çàêðûòà, è ñïåêòð ïðîåêòèðóåòñÿ íà âåðõíþþ è íèæíþþ ÷àñòü ùåëè.
Ïîëüçóÿñü ñîîòâåòñòâóþùèìè øêàëàìè, íàíåñåííûìè íà êðàÿõ äèàôðàãìû,
ìîæíî ïîëó÷èòü ñïåêòðîãðàììó, â ñðåäíåé ÷àñòè êîòîðîé áóäåò ñíÿòà ïîëîñà
öèàíà, à ñâåðõó è ñíèçó ñïåêòð æåëåçà. Ñïåêòð ñíèìàåòñÿ íà óçêóþ ïëàñòèíêó
(3,5 × 13 ñì) êîòîðàÿ óêðåïëÿåòñÿ â êàññåòå ñ ïîìîùüþ ñïåöèàëüíîãî âêëàäûøà.
Íà ïëàñòèíêå ìîæíî ñíÿòü ïàðó ñïåêòðîâ ïðè ïîìîùè äèàôðàãìû,
ñòàâÿ êàññåòó â ïîëîæåíèå 34 (äëÿ îäíîé ïàðû) è â ïîëîæåíèå 44 (äëÿ äðóãîé).
1 3 4 6 7 9 258
ÝÊÑÏÎÇÈÖÈÈ ÄËß ÑÚÅÌÊÈ ÂÀÌ ÑÊÀÆÅÒ ËÀÁÎÐÀÍÒ!
Ïîìíèòå, ÷òî ñïåêòð ñíèìàåòñÿ âî âòîðîì ïîðÿäêå, à øêàëà äëèí âîëí
íàíåñåíà äëÿ ïåðâîãî ïîðÿäêà, è íå çàáóäüòå ïîâåðíóòü ðåøåòêó íà
ñîîòâåòñòâóþùèé óãîë.
Ñïåêòðîãðàììà ñíèìàåòñÿ íà ïëàñòèíêó, êîòîðàÿ îáðàáàòûâàåòñÿ
ïðè êðàñíîì ñâåòå.
Ñïåêòðîãðàììà èçìåðÿåòñÿ íà êîìïàðàòîðå (ÈÇÀ -2), îïèñàíèå êîòîðîãî
âûäàåò ëàáîðàíò.
Ïðàêòè÷åñêèå óêàçàíèÿ.
Äàííûå ôîêóñèðîâêè ÄÔÑ-8:
Ïðîäîëüíîå ïåðåìåùåíèå - 11 ìì.
Ïîâîðîò - 6 ìì.
Øèðèíà ùåëè - 15 ìèêðîí.
Ïîëîæåíèå êàññåòû 34, 44.
ÂÍÈÌÀÍÈÅ !
1.Ñúåìêà ñïåêòðà ïðîâîäèòñÿ âî âòîðîì ïîðÿäêå, ò.å. íåîáõîäèìî
o
ïîâåðíóòü ðåøåòêó íà óãîë, ñîîòâåòñòâóþùèé 7770 A (øêàëà ïðèáîðà
o
äàåò îòñ÷åò ñ òî÷íîñòüþ äî 10 A ).
2.Ñïåêòð ñíèìàþò íà óçêóþ ïëåíêó ÐÔ-3 ( 3,5 × 13 ñì) , êîòîðàÿ
13
Ëàáîðàòîðíàÿ ðàáîòà ¹72
óêðåïëÿåòñÿ â êàññåòå ñ ïîìîùüþ ñïåöèàëüíîãî âêëàäûøà. Äëÿ ñîâìåùåíèÿ
âûõîäíîé ïðîðåçè ïðèáîðà ñ ñåðåäèíîé ïëàñòèíêè, êàññåòó íàäî ïîñòàâèòü
â ïîëîæåíèå 37.
ÇÀÄÀÍÈÅ .
1.Îòüþñòèðîâàòü òðåõëèíçîâóþ êîíäåíñîðíóþ ñèñòåìó.
2.Ñôîòîãðàôèðîâàòü ñïåêòð óãîëüíîé äóãè ìåæäó ñïåêòðàìè æåëåçà, ïîëüçóÿñü
äëÿ ýòîãî ôèãóðàëüíîé äèàãðàììîé.
o
3.Îïðåäåëèòü ÷àñòîòû ëèíèé (â ñì-1 ) ïîëîñû 3883 A .
4.Îïðåäåëèòü âðàùàòåëüíûå êâàíòîâûå ÷èñëà ëèíèé P è R âåòâåé, èñïîëüçóÿ
ïðè ýòîì ñõåìó èõ îáðàçîâàíèÿ (ðèñ.5) è ñðàâíèâàÿ ïîëó÷åííûé ñïåêòð ñ
èçîáðàæåíèåì íà ðèñ.6.
5.Íà îñíîâå (19) è (20) íàéòè âðàùàòåëüíûå ïîñòîÿííûå B′ è B′′ äëÿ âåðõíåãî
è íèæíåãî ýíåðãåòè÷åñêèõ ñîñòîÿíèé.
6.Ïî ôîðìóëå (2) îïðåäåëèòü ìîìåíò èíåðöèè ìîëåêóëû öèàíà äëÿ îáåèõ
ýíåðãåòè÷åñêèõ ñîñòîÿíèé.
ÎÒ×ÅÒ ÄÎËÆÅÍ ÑÎÄÅÐÆÀÒÜ:
1.Ïîëíóþ îïòè÷åñêóþ ñõåìó óñòàíîâêè ñ óêàçàíèåì õîäà ëó÷åé ê íåé.
2.Ñïåêòðîãðàììó.
3.Ðåçóëüòàòû èçìåðåíèé ñïåêòðîãðàììû íà êîìïàðàòîðå.
4.Ãðàôè÷åñêîå èçîáðàæåíèå ðàñøèôðîâàííîé ïîëîñû â øêàëå ÷àñòîò ñ
óêàçàíèåì âðàùàòåëüíûõ êâàíòîâûõ ÷èñåë è âåòâåé ïîëîñû.
5.Ðàñ÷åò âðàùàòåëüíûõ ïîñòîÿííûõ è ìîìåíòîâ èíåðöèè ìîëåêóëû.
6.Îöåíêó òî÷íîñòè ïîëó÷åííûõ ðåçóëüòàòîâ.
ËÈÒÅÐÀÒÓÐÀ
1. Ñ. Ý. Ôðèø - Êóðñ îáùåé ôèçèêè, ò. III.
2. Ãåðöáåðã. - Ñòðîåíèå è ñïåêòðû äâóõàòîìíûõ ìîëåêóë, ÃÒÒÈ, 135.
14