Документ 234702

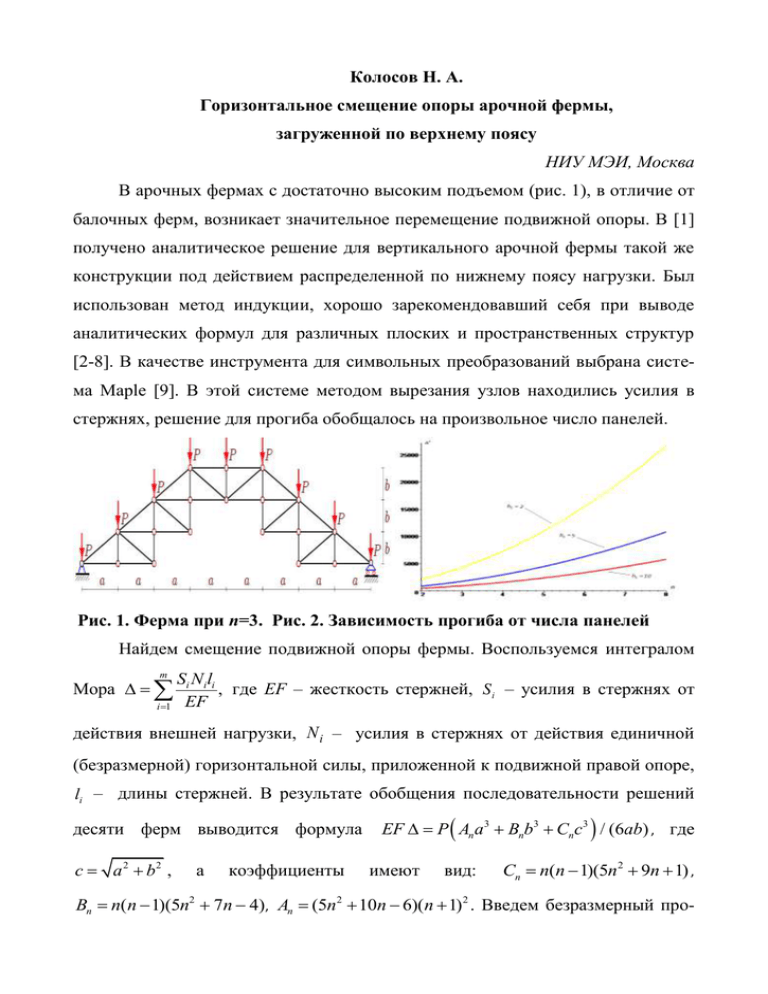
Колосов Н. А.
Горизонтальное смещение опоры арочной фермы,
загруженной по верхнему поясу
НИУ МЭИ, Москва
В арочных фермах с достаточно высоким подъемом (рис. 1), в отличие от
балочных ферм, возникает значительное перемещение подвижной опоры. В [1]
получено аналитическое решение для вертикального арочной фермы такой же
конструкции под действием распределенной по нижнему поясу нагрузки. Был
использован метод индукции, хорошо зарекомендовавший себя при выводе
аналитических формул для различных плоских и пространственных структур
[2-8]. В качестве инструмента для символьных преобразований выбрана система Maple [9]. В этой системе методом вырезания узлов находились усилия в
стержнях, решение для прогиба обобщалось на произвольное число панелей.
Рис. 1. Ферма при n=3. Рис. 2. Зависимость прогиба от числа панелей
Найдем смещение подвижной опоры фермы. Воспользуемся интегралом
m
Мора   
i 1
Si Nili
, где EF – жесткость стержней, S i – усилия в стержнях от
EF
действия внешней нагрузки, N i – усилия в стержнях от действия единичной
(безразмерной) горизонтальной силы, приложенной к подвижной правой опоре,
li – длины стержней. В результате обобщения последовательности решений
десяти ферм выводится формула
c  a 2  b2 ,
а
коэффициенты
EF   P  An a 3  Bnb3  Cn c3  / (6ab) , где
имеют
вид:
Cn  n(n  1)(5n2  9n  1) ,
Bn  n( n  1)(5n2  7n  4), An  (5n2  10n  6)(n  1) 2 . Введем безразмерный про-
гиб  '  EF  / P0 , где P0  (2n  3) P – суммарная нагрузка на ферму. Зафиксируем пролет фермы и ее высоту L  an, b0  bn . Зависимости прогиба от числа
панелей отображены в графиках на рис. 2 при L  30 м.
...
1. Волостнов Д. К. Формула для прогиба балочной фермы, загруженной по
нижнему поясу //Вестник научных конференций. 2015. № 2-2(2). Перспективы развития науки и образования: по материалам международной
научно-практической конференции 31 октября 2015 г. Часть 2. С. 39-40.
2. Тиньков Д. В. Сравнительный анализ аналитических решений задачи о
прогибе ферменных конструкций //Инженерно-строительный журнал.
2015. №5(57). С. 66–73.
3. Кирсанов М.Н. Аналитический расчет, предельный и сравнительный анализ плоской балочной фермы// Научный вестник ВГАСУ. Строительство
и архитектура. 2015. №3(39). С. 86-93.
4. Кирсанов М.Н. Аналитический расчет прогиба плоской решетчатой фермы
треугольного
очертания//
Trends
in
Applied
Mechanics
and
Mechatronics. М: Инфра-М, 2015. Т. 1. С. 28-30.
5. Кирсанов М.Н. Аналитический расчет пространственной стержневой регулярной структуры с плоской гранью // Строительная механика и расчет
сооружений. 2015. № 2. С. 2–6.
6. Кирсанов М.Н. Дискретная модель свайного фундамента // Инженерностроительный журнал. 2015. №3(55). С. 3–9.
7. Кирсанов М.Н. Математическая модель балочной фермы с элементами
упрочнения // Инженерно-строительный журнал. 2015. №4(56). С. 38–44.
8. Кирсанов М.Н. Жесткость торсионной подвески микромеханического
волнового твердотельного гироскопа // Приборы и системы. Управление,
контроль, диагностика. 2015. № 3. С. 18–22.
9. Кирсанов М. Н. Maple и Maplet. Решение задач механики. СПб.: Изд-во
Лань, 2012. 512 с.