Пример расчёта плоской статически неопределимой фермы

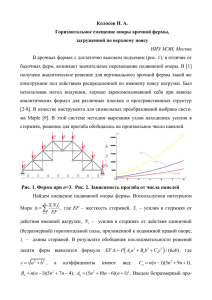
Практическое занятие 1,2
Пример расчёта плоской статически неопределимой
фермы методом сил
Рассмотрим плоскую ферму (рис. 1).
P
P/2 1
P
2
3
3b
4
5
4b
6
4b
Рисунок 1 Расчётная схема фермы
По формуле (1.2) определяем степень статической неопределимости i
(число узлов j = 6, число элементов m = 11, число наложенных опорных связей r
= 3):
i  m  2  j  r  11  2  6  3  2 .
Итак, ферма дважды статически неопределима – имеем две «лишние
связи». Выберем основную статически определимую систему, удалив две связи:
разрежем стержни 1 – 5 и 3 – 5. Действие отброшенных связей заменим
неизвестными реакциями в этих связях – силами в стержнях Х1 и Х2 – получим
статически определимую систему (рис. 2), эквивалентную исходной статически
неопределимой, с неизвестными силами Х1 и Х2.
P
P/2 1
P
2
Х1
3
Х2
4
5
6
Рисунок 2 Эквивалентная система
2
Х1 и Х2 найдём из условий эквивалентности полученной статически
определимой системы и исходной статически неопределимой, которые
выражают отсутствие перемещений в направлении отброшенный связей (т.е.
отсутствие взаимного перемещения сечений в точках разреза стержней 1 – 5 и 3
– 5 от действия внешней нагрузки и неизвестных сил Х1 и Х2 в стержнях 1 – 5 и
3 – 5:
11 X1  12 X 2  1P  0 

 21 X1   22 X 2   2 P  0
Коэффициенты  ij и свободные члены  iP - взаимное смещение краёв
сечений в точках разреза стержней 1 – 5 и 3 – 5 от единичных и внешней
нагрузок соответственно показаны на рис. 3, 5, 6.
Рассмотрим первое единичное нагружение (рис. 1.21) и определим осевые
силы, действующие в стержнях фермы (рис.1.22).
1
2
3
1
δ11
δ21
4
5
6
Рисунок 3 - Перемещения от первого единичного нагружения
Вырежем первый узел (рис. 4).
1
N1-4
0.6
N1-2 0.8
2
1
1
0
0
3
0
0
0
0
N2-4
1
N2-5
0.6
4
0
N5-4
5
6
Рисунок 4 - Силы в стержнях фермы от первого единичного нагружения
Так как косинус угла 5-1-2 равен 0.8, а угла 4-1-5
равновесия для первого узла запишутся:
0.6, то уравнения
©Учебный центр «Эрудит», www.childrensafety.jimdo.com , © Maria Bezmelnitsina Collé
3
F
y
 0 : - 1  0.6  N1-4  0
 Fх  0 :
1  0.8  N1-2  0
N1-4  0.6
N1-2  0.8
Далее рассмотрим третий узел. Он не нагружен и в нём соединяются два
стержня (третий стержень рассечён и усилие в нём равно нулю). Поэтому
осевые силы в этих двух стержнях равны нулю. Аналогично равны нулю и
осевые силы в двух стержнях в узле 6. Теперь рассмотрим второй узел:
 Fх  0 : 0.8  N 2-4  0.8  0
 F  0 : - 1  0.6  N  0
y
2 -5
N 2- 4  1
N 2-5  0.6
Из рассмотрения равновесия 5 узла следует:
 Fх  0 : - 1  0.8  N 5-4  0
N 5-4  0.8 .
Для второго единичного нагружения значения сил можно записать, очевидно,
не рассматривая равновесия узлов (будет в этом случае загружена правая
половина фермы).
1
2
3
1
δ22
δ12
4
5
6
Рисунок 5 Перемещения от второго единичного загружения
©Учебный центр «Эрудит», www.childrensafety.jimdo.com , © Maria Bezmelnitsina Collé
4
P
P/2 1
P
2
3
Δ1P
Δ2P
4
X4
5
6
Y4
Y6
Рисунок 6 Перемещения от внешнего нагружения
Определим осевые силы, возникающие в стержнях фермы, от внешнего
нагружения (рис. 6, 7), для чего сначала определим реакции опор.
 Fx  0 :
 М4  0 :
F
y
Х4  P / 2  0
11
8b  Y6  3b  P / 2  P  4b  0 Y6  P
16
11
Y4  P  P  P  0
16
 0:
Х 4  P / 2
Y4 
Рассмотрим равновесие первого узла (рис. 7).
F  0 : - P  N  0
 Fх  0 : P/2  N1-2  0
y
1- 4
Рассмотрим равновесие 4-го узла:
 Fy  0 : - P  21P / 16  N 4-2  0.6  0
 Fх  0 :
- P/2 - 25P/48   0.8  N 4-5  0
N1-4  P
N1-2  P / 2
N 4-2  25P / 48
N 4-5  11P / 12
©Учебный центр «Эрудит», www.childrensafety.jimdo.com , © Maria Bezmelnitsina Collé
21
P
16
5
P
P/2 1
N1-2 P/2
P
2
0
0
3
N1-4
25Р/48
55/48
Р
0
N6-2 0
4
P/2
21P/16
N4-5 11Р/12 5 N5-6 N6-5 6
11P/16
Рисунок 7 Определение осевых сил в стержнях
Так как в 3-ем ненагруженном узле сходятся два стержня и,
следовательно, осевые силы в них равны нулю.
Из равновесия пятого узла следует:
N 52  0 ; N 56  N 45  11P / 12
Рассмотрим проекцию на вертикальную ось сил для 6-го узла:
F
y
 0 : 11P / 16  N 2-6  0.6  0
N 2-6  55P / 48
Результаты определения сил в основной системе фермы от единичных
загружений и от внешней нагрузки, а также подсчёт коэффициентов и
свободных членов системы канонических уравнений метода сил приведены в
таблице.
Итак, система канонических уравнений метода сил запишется:
401 
P
480 
,
2783 
1.08X1  12.28X 2 
P
480 
12.28X1  1.08X 2 
СтерНагружение
L N1 N1L
жень
1
2
Р
N1-2 -0.8 0
-1/2 4
2.56
N1-4 -0,6 0
-1
3
1.08
N1-5
1
0
0
5
2.5
N2-4
1
0 -25/48 5
2.5
N2-5 -0.6 -0.6
0
3
1.08
N2-6
0
1 -55/48 5
0
N2-3
0 -0.8
0
4
0
N1 N2L
N2 N2L
N1 NPL
N2 NPL
0
0
0
0
1.08
0
0
0
0
0
0
1.08
2.5
2.56
1.6P
1.8P
0
-125P/96
0
0
0
0
0
0
0
0
-275/96P
0
©Учебный центр «Эрудит», www.childrensafety.jimdo.com , © Maria Bezmelnitsina Collé
6
N3-6
0 -0.6
0
3
N3-5
0
1
0
N4-5 -0.8 0
11/12 4
N5-6
0 -0.8 11/12 4
Коэффициенты и свободные
члены системы уравнений
решение которого
0
0
2.56
0
12.28
δ11
0
0
0
0
1.08
δ12
1.08
2.5
0
2.56
12.28
δ22
0
0
0
0
-176P/60
0
0
-176/60P
-401P/480 -2783/480P
Δ1P
Δ2P
X1  23983 P/897792  0.02671P
X 2  421777 P/897792  0.46979P
Осевые силы в стержнях исходной статически неопределимой ферме
определяются по формуле
N  N P  N1  X1  N 2  X 2
что даёт следующие значения осевых сил в стержнях фермы:
Стержень
N1-2
N1-4
N1-5
N2-4
N2-5
N2-6
N2-3
N3-6
N3-5
N4-5
N5-6
X1 = 1
-0.8
-0,6
1
1
-0.6
0
0
0
0
-0.8
0
Нагружение
X2 = 1
0
0
0
0
-0.6
1
-0.8
-0.6
1
0
-0.8
Сила
Р
-P/2
-P
0
-25P/48
0
-55P/48
0
0
0
11P/12
11P/12
©Учебный центр «Эрудит», www.childrensafety.jimdo.com , © Maria Bezmelnitsina Collé
-0.521P
-1.016P
0.027P
-0.494P
-0.298P
-0.676P
-0.376P
-0.282P
0.47P
0.895P
0.541P