определение показателя адиабаты газов при помощи

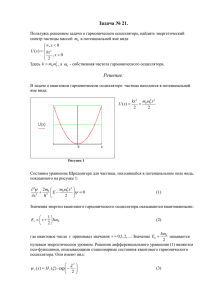
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального
образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ»
Утверждаю
Директор ФТИ
__________О.Ю. Долматов
«__» __________2015 г.
Н.С. Кравченко, О.В. Громова, В.В. Шамшутдинова
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ГАЗОВ
ПРИ ПОМОЩИ ОСЦИЛЛЯТОРА
ФЛАММЕРСФЕЛЬДА
Методические указания к выполнению лабораторной работы МФ-03
по курсу «Общая физика» для студентов всех специальностей
Издательство
Томского политехнического университета
2015
УДК 53(076.5)
ББК 22.3Я73
К 772
Кравченко Н.С.
К772 Определение показателя адиабаты газов при помощи осциллятора Фламерсфельда: методические указания по выполнению лабораторной работы по курсу «Общая физика» для студентов всех специальностей / Н.С.
Кравченко, О.В. Громова, В.В., Шамшутдинова; Томский политехнический университет.- Томск: Изд-во Томского политехнического университета, 2014. – 11 с.
УДК 53(075.8)
ББК 22.3Я73
Учебно-методическое пособие рассмотрено и рекомендовано к изданию
методическим семинаром кафедры теоретической и экспериментальной
физики ФТИ «__»___________20___г.
Зав. кафедрой
проф., доктор физ.-мат. наук
В.Ф.Пичугин
Председатель учебно-методической комиссии
С.И. Борисенко
Рецензент
Доктор физико-математических наук, профессор Томского
государственного университета С.И. Борисенко
 ФГБОУ ВПО НИ ТПУ, 2015
 Кравченко Н.С., Громова О.В.. Шамшутдинова
В.В. 2015
 Оформление. Издательство Томского
политехнического университета, 2015
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ГАЗОВ ПРИ
ПОМОЩИ ОСЦИЛЛЯТОРА ФЛАММЕРСФЕЛЬДА
Цель работы: определение показателя адиабаты для воздуха при помощи
осциллятора Фламмерсфельда.
ТЕОРЕТИЧЕСКОЕ СОДЕРЖАНИЕ
Термодинамическая система - совокупность макроскопических тел, обменивающихся веществом и энергией как друг с другом, так и с внешней средой
(т.е. любое макроскопическое тело или система тел). Замкнутой системой
называется система, не обменивающаяся веществом с окружающими систему
телами. Изолированной системой называется система, не взаимодействующая
с внешними телами (окружающей средой). Физические величины, характеризующие состояние термодинамической системы называются параметрами состояния или термодинамическими параметрами (объем, давление, температура,
плотность и т.д.). Уравнение, связывающее между собой параметры состояния
термодинамической системы, называется уравнением состояния. Простейшей
моделью термодинамической системы является идеальный газ. Для идеального
m
газа уравнение состояния - это уравнение Менделеева-Клапейрона PV  RT .

Если параметры системы при ее взаимодействии с окружающими телами
не изменяются с течением времени, то состояние системы называют стационарным.
Величины, не зависящие от предыстории системы и однозначно определяющие состояние системы в данный момент, называются функциями состояния.
Процессом называется переход системы из одного состояния в другое, который сопровождается изменением хотя бы одного из параметров состояния.
Уравнение, определяющее изменение параметров системы при переходе из одного состояния в другое, называется уравнением процесса.
Равновесные процессы – процессы, при которых скорость изменения термодинамических параметров бесконечно мала, т.е. изменение термодинамических параметров происходит за бесконечно большие времена. Это модель, т.к.
все реальные процессы – неравновесные. Равновесный процесс – процесс, который проходит через последовательность равновесных состояний.
В термодинамике используется особый метод изучения явлений – термодинамический метод. Предметом термодинамики является анализ поведения
термодинамических систем, т. е. систем, состоящих из большого числа частиц.
Одно из важных положений термодинамики, основанное на массе опытных
фактов, гласит: любая система, будучи помещенной в неизменные однородные
внешние условия, обязательно приходит в равновесие, т.е. в определенное состояние, в котором она и будет находиться сколь угодно долго.
3
В основу термодинамики положено три основных закона (первое, второе и
третье начала термодинамики), являющиеся обобщением громадного фактического материала.
Первое начало термодинамики
Рассмотрим замкнутую термодинамическую систему. Например, идеальный газ в цилиндре с подвижным поршнем, состояние которого определятся
термодинамическими параметрами P (давление газа), V (объем газа), T (темпеm
ратура), m (масса газа) или количество молей (  , μ – молярная масса).

Идеальный газ – газ, молекулы которого принимаются за материальные точки
и для которого можно пренебречь потенциальной энергией межмолекулярного
притяжения по сравнению с их кинетической энергией.
1.
Важнейшей характеристикой термодинамической системы в равновесном состоянии является внутренняя энергия. Внутренняя энергия U термодинамической системы равна сумме кинетической энергии внутреннего движения и потенциальной энергии взаимодействия составляющих систему частиц
(молекул, атомов, электронов и т.д.). Такое представление соответствует представлениям молекулярно-кинетической теории о строении и свойствах вещества. В идеальном газе молекулы обладают только кинетической энергией,
среднее значение которой определятся температурой. Средняя кинетическая
i
энергия молекулы, имеющей i степеней свободы, равна Ek  kT , где
2
-23
k=1,38·10 Дж/К.
Числом степеней свободы называется наименьшее число независимых координат, которое
необходимо ввести, чтобы определить положение тела в пространстве.
Внутренняя энергия U идеального газа – это сумма кинетических энергий всех его молекул. Внутренняя энергия U 0 одного моля идеального газа:
U 0  E к N A , где E к – средняя кинетическая энергия одной молекулы газа, N A –
число Авогадро (число молекул в одном моле). Так как постоянная Больцмана
R
i
i R
i
, то
k
U 0  E к N A  kTN A 
TN A  RT .
2
2 NA
2
NA
m
Если газ имеет массу m , то
– число молей, где  – масса моля, и внут-

mi
RT .
2
Внутренняя энергия идеального газа зависит от температуры газа. Изменение
внутренней энергии идеального газа определяется изменением температуры и
не зависит от процесса, при котором это изменение произошло.
mi
RT , где T – изИзменение внутренней энергии идеального газа: U 
2
менение температуры. Внутренней энергией U системы называется функция
состояния, изменение которой при любом процессе однозначно определяет изменение состояния системы.
ренняя энергия газа выражается формулой:
4
U
2.
Обмен энергией замкнутой системы с окружающими телами может
осуществляться двумя различными способами: при совершении работы и при
теплообмене. Изменение внешних параметров термодинамической системы
(например, изменение объема газа) может осуществляться вследствие взаимодействия с телами, окружающими систему. При этом внешние силы совершают
работу Aв неш . Если аналогичное изменение параметров системы произведено
самой системой, то при этом системой совершена работа А. При статических
(или квазистатических) процессах A   Aвнеш . Таким образом, мерой передачи
энергии является работа. Элементарная работа, совершаемая системой в любом
процессе равна A  PdV , где P – давление, dV – изменение объема.
3.
Состояние термодинамической системы можно изменить (например, изменением объема газа) и без совершения работы. Системе в результате
теплообмена можно сообщить некоторое количество теплоты Q. Количеством
теплоты Q называется энергия, полученная термодинамической системой путем
теплообмена, то есть без совершения над системой работы внешними силами.
Если состояние заключенной в жесткую оболочку термодинамической системы
не изменяется при нагревании или охлаждении тел, находящихся вне оболочки,
и постоянных внешних параметрах системы, такая оболочка называется адиабатической. Изменить состояние системы, заключенной в адиабатическую
оболочку, можно только путем изменения внешних параметров системы
(например, изменить объем) внешними силами. Система тел, заключенная в
адиабатическую оболочку, называется адиабатически изолированной.
Рассмотрим газ в теплоизолированном цилиндре (адиабатически изолированную систему). Цилиндр разделен жесткой теплопроводящей перегородкой
на два отсека C и D. Объём отсека С поддерживается постоянным, над этой частью газа не может быть совершена работа. Объём отсека D может меняться
при помощи подвижного поршня. За счет теплопроводящей перегородки отсеки
могут обмениваться внутренней энергией.
Если в результате совершения над
Жёсткая
Подвижный
системой C+D внешними силами работы
перегородка поршень
в неш
A12
, система перешла из произвольного
состояния 1 в произвольное состояние 2,
C
D
то при этом изменилась внутренняя энергия
системы.
Тогда
внеш
CD
CD
C
D
C
D
A12  U 2  U1  U 2  U 2  U1  U1 .
Тогда U1C  U 2C  U 2D  U1D  A12внеш , изменение внутренней энергии газа в отсеке С произошло за счет теплообмена без
совершения работы и равно количеству теплоты Q, полученному газом через
жёсткую перегородку. Обозначим U 2D  U1D  U изменение внутренней энергии
газа в отсеке D. Тогда получим:
внеш
Q  U  A12
. Это равенство является математическим выражением первого начала термодинамики. Оно подразумевает, что полученное термодинами-
5
ческой системой количество теплоты Q равно приращению её внутренней
в неш
энергии U за вычетом работы над системой внешних сил A12
.
Если переход системы из состояние 1 в состояние 2 является равновесным,
в неш
то A12
= – A, где А – работа системы против внешних сил. В таком случае
Q  U  A .
Равенство подразумевает, что полученное термодинамической системой в
равновесном процессе количество теплоты Q идет на приращение его внутренней энергии U и совершение системой работы А над внешними телами.
Для бесконечно малого (элементарного) равновесного процесса уравнение
принимает вид: Q  U  A  dU  PdV . Это выражение представляет собой
дифференциальную форму записи первого начала термодинамики.
Первое начало термодинамики – это закон сохранения энергии. Оно устанавливает закон взаимопревращения теплоты, энергии и работы.
Адиабатический процесс
Адиабатическим называется процесс, в котором термодинамическая система не обменивается теплотой с окружающими телами: Q  0 -уравнение
адиабатического процесса.
Адиабатический процесс можно осуществить двумя способами:
 осуществить хорошую теплоизоляцию, что практически довольно
трудно сделать;
 провести процесс настолько быстро (но так, чтобы процесс оставался
равновесным), чтобы не успел произойти теплообмен с окружающей средой.
Найдем уравнение, связывающее параметры идеального газа в равновесном адиабатическом процессе. В соответствии с первым началом термодинаmi
mi
RdT  PdV  0 , или PdV  
RdT . Из уравнения
мики: Q  dU  A 
2
2
m RT
состояния PV  RT выразим P через объем V и температуру T: P 
. Ис V
m RT
mi
dV
i dT
dV  
RdT , тогда
пользуя это уравнение, имеем
или

 V
2
V
2 T
dT
2 dV
dT
2 dV

 
. Проинтегрируем данное выражение: 
. После интеT
i V
T
i V
2
грирования получим: ln T  ln V  ln const .
i
C
2
i2
2
 1  , отсюда    1 , где  - коВведем обозначения:   P 
i
CV
i
i
эффициент Пуассона или показатель адиабаты, равный отношению теплоемкоi2
R и теплоемкости при постоянном
стей при постоянном давлении C P 
2
6
i
объеме CV  R . Показатель адиабаты зависит только от числа степеней сво2
боды молекул газа.
2
Тогда уравнение ln T  ln V  ln const можно представить в виде
i
 1
TV  const - при увеличении объема идеального газа в адиабатических условиях его температура понижается.
Используя уравнение Менделеева-Клапейрона полученное соотношение
можно записать в виде: PV   const - уравнение Пуассона для идеального газа
или уравнение адиабаты.
Экспериментальная установка
8
5
2
1
7
4
6
3
Экспериментальная установка для определения показателя адиабаты газов
при помощи осциллятора Фламмерсфельда
1 – колба с осциллятором Фламмерсфельда;
2 – стеклянный баллон;
3 – клапан регулирования воздуха (редукционный клапан);
4 – насос;
5 – световой барьер со счетчиком;
6 – секундомер;
7 – осциллятор (пластмассовое тело);
8 – стеклянная трубка.
В качестве рабочего вещества в данной работе используется воздух, поэтому давление, необходимое для проведения эксперимента, нагнетается насосом
7
(4). Стеклянная трубка (8) вертикально вставлена в колбу (1). Осциллятор
(пластмассовое тело) (7) помещается внутрь стеклянной трубки (как показано на
рисунке). На стеклянной трубке имеется щель (отверстие) и два синих кольца. Луч
света из светового барьера (5) направляется в центр трубки. Триггерный порог
светового барьера устанавливается автоматически после включения нажатием
кнопки RESET (Сброс). При установлении режима COUNT (Счет), счетчик светового барьера (8) фиксирует количество колебаний n осциллятора. Если включить насос (4) и открыть редукционный клапан (3), осциллятор вследствие избыточного давления в колбе начнет двигаться вверх. При своем движении он пересекает щель, через которую воздух из колбы начнет выходить. Давление в колбе
быстро уменьшится, и осциллятор начнет падать вниз. Осциллятор колеблется в
некотором объеме газа в стеклянной трубке. При помощи редукционного клапана (3) можно добиться, чтобы амплитуда колебания осциллятора была постоянной. Осциллятор должен колебаться симметрично относительно синих колец на
стеклянной трубке.
Важно: вставляйте осциллятор в трубку только после того, как выпустили
поток газа (давление в баллоне (2) примерно равно атмосферному). Редукционный
клапан необходимо открывать осторожно. При резком открывании клапана осциллятор может быть выброшен из трубки, поэтому слегка прикрывайте рукой
край трубки, пока не установится постоянная амплитуда колебаний. Если осциллятор вклинивается в нижний конец трубки, снимите стеклянную трубку и осторожно отсоедините осциллятор при помощи тупого конца карандаша.
Рабочие формулы
На рисунке изображены различные положения осциллятора в стеклянной
трубке при его движении. В стеклянной трубке на боковой
P0
поверхности имеется отверстие (точка 0 на рисунке). Если
2
осциллятор поместить в трубке ниже этого отверстия (положение 1 на рисунке), то давление воздуха в колбе равно
mg
x
P  P0  2 , где P0 – атмосферное давление, m – масса осr
циллятора, r 2  S - площадь поперечного сечения осцилля0
тора. В этом положении осциллятор находится во взвешенx
ном состоянии, а газ в колбе характеризуется параметрами P
P0
– давление газа, V – объем газа в колбе. Чтобы заставить
1
осциллятор двигаться вверх, необходимо создать в колбе

mg
небольшое избыточное давление газа dP´, которое создает
насос. Уравнение движения осциллятора тогда можно заP,V
d 2x
писать: m 2  PS . Если ∆P´ - постоянная величина
dt
(определяется интенсивностью нагнетания воздуха в колбу насосом), то сила
F´, действующая на осциллятор, величина постоянная. Под действием постоянной силы осциллятор движется поступательно и прямолинейно с постоян8
ным ускорением. Однако, в точке 0 осциллятор открывает отверстие, и давление в трубке нормализуется (становится равным P0), ∆P´ становится равным
нулю. Осциллятор в точке 0 имел максимальную скорость и максимальную кинетическую энергию. Он по инерции пролетает до точки 2 и под действием силы тяжести начинает падать вниз: от точки 2 до точки 0 – свободное падение,
от точки 0 до точки 1 – сжимая газ, пока давление газа не станет равным P.
Далее процесс повторяется. Таким образом, осциллятор совершает незатухающие колебания.
Однако колебательное движение осциллятора изменяет состояние газа в
колбе. При движении осциллятора вверх до точки 0 газ расширяется, а при
движении вниз от точки 0 до точки 1 – газ сжимается. Процессы расширения и
сжатия газа - периодические процессы. Таким образом, колебательное движение осциллятора можно связать с периодическим быстро протекающим процессом сжатия и расширения газа.
Рассмотрим колебательное движение осциллятора, вызванное изменением состояния газа при его движении из положения 1-0-2 вверх и обратно.
1. Движение осциллятора вверх из положения 1 в положение 0. При перемещении осциллятора вверх на величину x, объем газа в трубке (колбе) увеличивается на величину ∆V=S·x, а давление газа уменьшается на величину ∆P.
Изменение давления газа приводит к появлению дополнительной силы F, величина которой пропорциональна ∆P, а направление этой силы противоположно
смещению x осциллятора.
Тогда уравнение движения осциллятора согласно второму закону Ньютоd 2x
на можно записать: m 2  PS .
(1)
dt
Так как движение осциллятора происходят сравнительно быстро ( но не
настолько, чтобы процессы стали неравновесными), то изменение объема газа
можно рассматривать как адиабатическое и воспользоваться уравнением
адиабаты: PV   const , где V – объем газа.
P
В результате дифференцирования получаем: dP  
(2) или
dV
V
P
P   V
V
Заменяя в (2) V  r 2  x в (1) получаем дифференциальное уравнение
движения осциллятора вверх из 1 в 0 (уравнение гармонических колебаний осциллятора):
d 2 x  2 r 4 P

x0
(3)
mV
dt 2
2. Движение осциллятора от точки 0 до точки 2 и обратно. В точке 0 траектории движения осциллятор за счет избыточного давления, создаваемого
насосом, имеет максимальную скорость. Осциллятор при своем движении открывает отверстие на боковой поверхности трубки, в результате чего давление
в колбе нормализуется и становится равным P0. Поэтому осциллятор от точки 0
9
до точки 2 пролетает по инерции. За счет кинетической энергии он поднимается на высоту x относительно точки 0. Затем начинает свободно падать до точки
0, где снова перекрывает отверстие.
3. Движение осциллятора от точки 0 вниз до точки 1. При свободном падении от точки 2 до точки 0 осциллятор приобрел скорость (кинетическую
энергию), поэтому при движении вниз от точки 0 он будет сжимать газ и уравнение движения осциллятора будет аналогично уравнению (1) и, следовательно, уравнению (3).
Таким образом, колебательное движение осциллятора , вызванное измеd 2 x  2 r 4 P
нением состояния газа, описывается уравнением: 2 
x  0.
mV
dt
Данное уравнение представляет собой дифференциальное уравнение гарd 2x
монических колебаний типа 2   2 x  0 (4),
dt
решением которого является уравнение x  A  cos(t  0 ) , где А – ам2
плитуда колебания,  
- угловая частота колебания, T – период колебания,
T
φ0 – начальная фаза.
Из сравнения уравнения (3) и (4) имеем  
 2 r 4 P
mV
.
2
2
 2 r 4 P
Так как  
, то
.

T
T
mV
4mV
mg
Отсюда   2 4 ,
(5) ,
где P  P0  2 .
r
T Pr
Таким образом, для экспериментального определения показателя адиабаты, необходимо измерить период T гармонических колебаний осциллятора.
Порядок выполнения работы
1. Взвесьте осциллятор и определите массу m.
2. Измерьте микрометром диаметр 2r осциллятора (не менее 5 раз). Поскольку результат в значительной мере зависит от точности данного измерения, вычислите
среднее значение по результатам нескольких измерений. Результаты измерений
запишите в таблицу.
3. Объем газа в колбе (объем осциллятора) указан на установке (V= 1,14·10-3
м3).
4. Включите световой барьер. Направьте луч света из светового барьера (5) в
центр трубки. Триггерный порог светового барьера устанавливается автоматически после включения нажатием кнопки RESET (Сброс). Выберите количество колебаний n осциллятора, установив рабочий режим COUNT (Счет).
5. Включите насос (4) и откройте редукционный клапан (3), осциллятор вследствие избыточного давления в колбе начнет двигаться вверх. Чтобы осциллятор
не вылетел из трубки, слегка прикройте рукой край трубки, пока не устано10
вится постоянная амплитуда колебаний. При своем движении он пересекает
щель, через которую воздух из колбы начнет выходить. Давление в колбе быстро
уменьшится, и осциллятор начнет падать вниз. Осциллятор колеблется в некотором объеме газа в стеклянной трубке. При помощи редукционного клапана (3)
можно добейтесь, чтобы амплитуда колебаний осциллятора была постоянной и
осциллятор совершал колебания между синими кольцами, нанесенными на трубке.
6. Когда колебания установятся, включите секундомер и определите время t
для числа n колебаний. Обратите внимание, что счетчик реагирует на
движение осциллятора вверх и вниз, то есть фиксирует количество полу2t
периодов колебаний. Определите период установившихся колебаний: T  .
n
7. При помощи барометра определите атмосферное давление P0.
4mV
8. Определите показатель адиабаты для воздуха:  
.
mg 4
2
T ( P0  2 )r
r
i2
9. Сравните полученный результат с теоретическим:  
, где i – число
i
степеней свободы. Для воздуха i=5. Сделайте вывод.
10. Опыт повторите не менее 4 раз.
Таблица результатов измерений
№ Масса
,
осцилляп/ тора, (кг)
п
Диаметр
осциллятора 2r,
(м)
Объ
ем
газа
V,
(м3)
Атмосферное
давление
P0, (Па)
Вре Число
мя t, коле(сек) баний
n,
Период
колеба
ний T,
(сек)
Показатель
адиабаты γэкс-
Показатель
адиабаты γтео-
пер.
рет.
1
2
3
4
5
Контрольные вопросы
1.
Чем термодинамический подход к рассмотрению физических явлений отличается от молекулярно-кинетического и статистического?
2.
Разъясните понятие стационарного состояния. Что называют изолированной, замкнутой, адиабатической?
3.
Охарактеризуйте модель «идеальный газ».
4.
Сформулируйте первое начало термодинамики.
5.
Что такое внутренняя энергия системы?
6.
Запишите уравнение адиабатического процесса.
11
7.
Почему в условиях данного эксперимента, расширение газа при движении осциллятора можно считать адиабатическим?
12