Документ 2020233

Лекция 8.
Обсуждение результатов, полученных на предыдущей лекции.
Правило фаз для случая фазового равновесия:
f =c+2− p
Правило фаз для случая мембранного равновесия
f =c+2− p+ M
M - количество мембран. Каждая мембрана отменяет одно равенство в условиях
фазового равновесия. Появляется новая свободная переменная!
При выводе условия фазового равновесия использовался Второй закон в форме
( dU )V ,S ,n
i
≤0
Можно использовать формулировку для систем с постоянными температурой, давлением и
числами молей:
( dG ) p ,T ,n
i
≤ 0,
При любом выводе получаются одни и те же условия фазового равновесия. Использование
формулировки « через внутреннюю энергию» позволяет рассматривать систему, в которой в
начальный момент температуры и давления в фазах – разные. В случае энергии Гиббса мы с
самого начала должны предположить, что у системы одна температура и одно давление во
всех фазах, и можем доказать только, что обязаны выровняться химические потенциалы
компонентов во всех фазах. Задача получается более частной.
Однако, в лаборатории мы чаще имеем дело с закрытыми системами, находящимися при
постоянном давлении и температуре. Поэтому, как и в случае химического равновесия, при
рассмотрении задачи о фазовом равновесии удобна энергия Гиббса.
При движении к фазовому равновесию не только выравниваются температуры, давления и
химические потенциалы в фазах, но и самопроизвольно исчезают какие-то фазы, появляются
новые, и система неуклонно идет к минимуму внутренней энергии при постоянных S, V, ni,
к минимуму энергии Гиббса при постоянных p,T, ni. и т.д.
В результате, в состоянии равновесия будет существовать набор фаз, который соответствует,
положим, минимуму энергии Гиббса системы при заданных, постоянных p, T, ni.
Для этих фаз будут выполнены условия фазового равновесия.
Используем подобные соображения при рассмотрении фазовых диаграмм однокомпонентной
системы.
Лекция 8
1
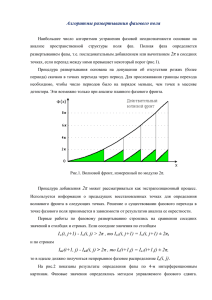
Диаграмма состояния воды. (рис. 1)
p − T описывает состояние равновесие вещества H 2O (1 моль)
при различных температурах и давлениях. Почему, например, при температуре T1 и давлении
p2 на диаграмме и в природе - лед? Потому что именно эта фаза имеет при T1 и p2
Диаграмма в координатах
минимальную энергию Гиббса.
Сравним, например, зависимости энергии Гиббса льда и водяного пара (газа) от давления и
температуры. Обе энергии Гиббса представляют собой поверхности в трехмерном
пространстве
Ggas = µ gas ( p, T ), Gice = µice ( p, T )
Вдоль линии пересечения поверхностей реализуется двухфазное равновесие лед- водяной
пар, потому что именно такой набор фаз обеспечивает минимальную энергию Гиббса
системы при данных давлениях и температурах.
Критическая точка
Вода жидкая
р2
Давление
Лёд
Водяной пар
Тройная
точка
Т1
273,16 К
Температура
373 К
547 К
Рис.1. Диаграмма состояния воды.
.
Диаграмма состояния серы (рис.2)
На диаграмме состояния серы присутствуют две твердые фазы: ромбическая сера S (ромб)
и моноклинная сера S(мон). Стрелкой показана линия фазового равновесия между двумя
твердыми фазами. Пересечение этой линии слева направо (увеличение температуры при
постоянном давлении) приводит к превращению ромбической серы в моноклинную.
Превращение сопровождается понижением энергии Гиббса.
Лекция 8
2
Рис.2. Диаграмма состояния серы.
График зависимости G
= µ = f(T, p = const)
Рассмотрим графики зависимости G = µ = f(T; p = const) в однокомпонентной системе
для твердой фазы и пара (рис. 3а). Ниже температуры T1 минимальную энергию Гиббса
имеет твердая фаза. При T1 выполняются условия фазового равновесия, пар и твердая фаза
имеют одинаковые химические потенциалы (энергии Гиббса). При дальнейшем увеличении
температуры твердая фаза должна исчезнуть. Всё вещество превращается в пар, потому, что у
пара меньшая энергия Гиббса.
На рисунке (3б) видим две точки фазового равновесия: T2 и T3 . Сначала тв. фаза плавится,
потом жидкая фаза превращается в пар. Процессы, которые мы наблюдаем при T1, T2 , T3
называются фазовыми переходами первого рода (рис. 3 а,б).
Построим теперь графики зависимости µ = f(p; T = const) (рис.3г). Они выглядят точно
также. При давлениях p1, p2, p3 в соответствии со Вторым законом одна фаза исчезает,
другая появляется. В точках фазового равновесия присутствуют две фазы.
Фазовые диаграммы р-Т есть проекции трехмерных диаграмм G = µ = f(T, p) на
плоскость р,Т.
Лекция 8
3
Рис. 3. Зависимость химических потенциалов твердой, жидкой и газовой фаз в
однокомпонентной системе от температуры и давления.
пар
(а)
тв.
(в)
(б)
(г)
.Диаграммы µ
= f(T; p = const) и р-Т для фосфора (рис. 4а,б)
Лекция 8
4
рис. 4а
T2
рис.4б
График зависимости химических потенциалов от температуры ( p = const ) для фосфора
показывает, что из твердых фаз в равновесии должна существовать только фаза фиолетового
фосфора (рис.4а). На рис.4а нет температур, при которых белый фосфор имел бы
наименьшую энергию Гиббса. Однако, в эксперименте наблюдаются обе твердые фазы.
Является ли это нарушением Второго закона термодинамики? Нет. Неравновесная фаза
должна разрушиться и перейти в равновесную, утверждает Второй закон. Но как скоро? На
этот вопрос у равновесной термодинамики нет ответа. Скорость превращения неравновесной
фазы в равновесную может быть очень малой. Фактически, неравновесная фаза становится
кинетически стабильной. Существование подобных фаз – очень распространенное явление.
Лекция 8
5
Неравновесные фазы, подобные белому фосфору, можно получить, быстро охлаждая
жидкость до температур, меньших
T2 (см. рис. 4а).
Получить белый фосфор из фиолетового невозможно. Такой процесс противоречил бы
Второму закону.
Если в системе существует несколько твердых фаз (как у серы и фосфора), то это явление
называется полиморфизмом. Если равновесной является только одна из твердых фаз (как у
фосфора), то возможен фазовый переход только в одну сторону (белый фосфор
→ фиолетовый фосфор). Говорят о явлении монотропии. Если существует несколько
равновесных твердых фаз и, следовательно, возможно фазовый переход «в обе стороны»,
фазовое равновесие (как у серы,
S ромб R S мон ), то говорят об энантиотропии.
Диаграмма р-Т и зависимости µ
= f(T, p = const) для углерода (рис.5а,б).
Р,Р,гПА
гПа
Жидкий
Жидкий
углерод
углерод
Алмаз
Алмаз
ВТ-ВД
синтез
ВТ-ВД
синтез
алмаза
алмаза
5 5
1.2*10
бар
1.2*10
бар
4200
КК
4200
Каталитический
синтез
Каталитический
синтез
алмаза
алмаза
Графит
Графит
CVD
синтез
CVD
синтез
алмаза
алмаза
Т,Т,КК
рис. 5а.
Лекция 8
6
рис.5б
При нормальном давлении графит является равновесной фазой при любых температурах
(рис.5б). Алмаз становится равновесной фазой только при очень высоких давлениях. В
этой области температур и давлений возможен синтез алмаза из графита. (рис.5а).
Э. стр. 251-253
Фазовый переход первого рода - это процесс перехода вещества из одной фазы в другую,
при котором претерпевают скачки первые производные химического потенциала. Фазовый
переход первого рода происходит при пересечении линии фазового равновесия. Эта линия
описывается уравнением Клаузиуса-Клапейрона
dp S ( II ) − S ( I )
=
dT V ( II ) − V ( I )
В точке фазового перехода первого рода выполняется условие фазового равновесия
T ( I ) = T ( II ) , p ( II ) = p ( I ) , µ1( II ) = µ1( I )
Фазовый переход первого рода чаще всего наблюдают при изменении температуры и
постоянстве давления ( p = const ), (см. рисунок 6а-г).
Ниже температуры T1 существует фаза
I , а выше T1 - фаза II . Химический потенциал
системы «переходит» с кривой для фазы I на кривую для фазы II (рис. 6а). При этом
(I )
( II )
энтропия скачком меняется от значения S (T1 , p ) до S
(T1 , p ) , (рис.6б). Объём
(I )
(T1 , p ) до V ( II ) (T1 , p ) , (рис.6в). Энтропия
системы изменится, соответственно, от V
и объём – первые производные химического потенциала, следовательно, они испытывают
скачок.
Лекция 8
7
⎛ dµ ⎞
⎛ dµ ⎞
,
S
=
−
=V
⎜
⎟
⎜
⎟
⎝ dT ⎠ p
⎝ dp ⎠T
рис. 7а
рис. 6а
рис. 6б
рис.7б
рис.7в
рис.6в
рис.6г
рис. 7г
Рис. 6(а-г) и 7 (а-г). Фазовые переходы первого и второго рода.
Лекция 8
8
График зависимости теплоемкости cp = f(T, p = const) вблизи фазового перехода
первого рода приводится на рисунке 6г. Поскольку в точке фазового перехода энтропия
терпит разрыв, а теплоемкость - это производная энтропии по температуре, то cp должна
уходить на бесконечность. Формально это так и получается: вы подаете в систему тепло, но
не можете изменить температуру системы, пока фаза I целиком не перейдет в фазу II :
δQ
dT
→∞
т.к. δ Q не равно нулю, а dT = 0. С другой стороны, часто рисуют «график с выколотой
точкой» и говорят о скачке теплоемкости при фазовом переходе первого рода. Сравниваются
теплоемкости фаз I и II в бесконечной близости от точки фазового перехода. «Скачок
теплоемкости» при фазовом переходе первого рода может быть как положительным, так и
отрицательным.
Пересечь линию фазового равновесия (осуществить фазовый переход первого рода) можно и
при ином способе изменения температуры и давления. Например, можно менять давление
при ( T = const ).
Примеры фазовых переходов первого рода
Прежде всего - это плавление, испарение, сублимация. Линии соответствующих фазовых
равновесий присутствуют, например, на диаграмме состояния воды. В современной
физической химии исследуют переходы между двумя твердыми фазами. На диаграмме
состояния серы - две твердых фазы. У многих органических веществ по четыре и более
твердых фаз. Существует понятие “soft crystal”, «мягкий кристалл», даже «жидкий кристалл».
Плавление органического кристалла как бы разбивается на несколько стадий.
Последовательно расшатывается кристаллическая решетка. Происходит несколько фазовых
переходов первого рода. На рис. 7 показано, как можно себе представить на молекулярном
уровне переход от твердого состояния к жидкому через жидкокристаллическую фазу.
Жидкие кристаллы - это. упорядоченная структура из длинных молекул, например,
производных холестирина. Характерные энтальпии фазового перехода:
Кристалл Æ жидкий кристалл: 220
Дж/грамм,
Жидкий кристалл Æ жидкость: 25
Дж/грамм
Фазовым переходом первого рода называют и денатурацию белка.
Размер фаз начинает играть роль, когда объекты становятся меньше ~100нм. Начиная с этого
размера, температуры фазовых переходов первого рода начинают меняться. Начинает играть
роль поверхностная энергия фаз.
Лекция 8
9
Кристалл
Жидкий кристалл
Жидкость
Рис.8. Расположение молекул в кристалле, жидком кристалле и жидкости.
Фазовые переходы второго рода, (рисунки 7 (а-г).
П. стр.129-132.
В жидком гелии при 2,2К впервые наблюдался фазовый переход, в котором не было
скачков энтропии и объема, но наблюдался скачок теплоемкости, т.е. первые производные
были непрерывны, а вторая производная менялась скачком. Согласно модели Эренфеста,
переход происходил при пересечении линии фазового равновесия. В точке перехода,
существовало равновесие между фазами:
T ( I ) = T ( II ) , p ( II ) = p ( I ) , µ1( II ) = µ1( I )
и выполнялось соотношение,
dp S ( II ) − S ( I )
= ( II )
dT V − V ( I )
(1)
Лекция 8
10
но числитель и знаменатель в уравнении Клаузиуса-Клапейрона равнялись нулю (не было
скачков энтропии и объёма!).
Рассчитаем dp/dT по правилу Лопиталя:
2 ( II )
2 (I )
⎛ ∂S ( II ) ⎞ ⎛ ∂S ( I ) ⎞
⎛
⎞
⎛
µ
µ ⎞
∂
∂
−
−
⎜
⎟ ⎜
⎟
⎜
⎜
2 ⎟
2 ⎟
dp ⎝ ∂T ⎠ p ⎝ ∂T ⎠ p ⎝ ∂T ⎠ ⎝ ∂T ⎠ ∆c p
1
=
=
=
×
dT ⎛ ∂V ( II ) ⎞ ⎛ ∂V ( I ) ⎞
T V ∆αV
⎛ ∂ 2 µ ( II ) ⎞ ⎛ ∂ 2 µ ( I ) ⎞
−
−
⎜ ∂T ⎟ ⎜ ∂T ⎟
⎜ ∂p∂T ⎟ ⎜ ∂p∂T ⎟
⎝
⎠p ⎝
⎠p ⎝
⎠ ⎝
⎠
(2)
В числителе стоит скачок теплоемкости, деленный на температуру перехода. В знаменателе скачок коэффициента теплового расширения, умноженный на объем, причем объем фаз
одинаков (нет скачка объема!). Это - скачки вторых производных химического потенциала.
Дифференцируя по давлению, получим:
⎛ ∂V ( II ) ⎞ ⎛ ∂V ( I ) ⎞
⎛ ∂S ( II ) ⎞ ⎛ ∂S ( I ) ⎞
⎜ ∂T ⎟ − ⎜ ∂T ⎟
⎜ ∂p ⎟ − ⎜ ∂p ⎟
dp ⎝
⎠p ⎝
⎠p
⎠T ⎝
⎠T = − ⎝
=
=
( II )
(I )
( II )
(I )
dT ⎛ ∂V ⎞ ⎛ ∂V ⎞
⎛ ∂V ⎞ ⎛ ∂V ⎞
−
⎜ ∂p ⎟ ⎜ ∂p ⎟
⎜ ∂p ⎟ − ⎜ ∂p ⎟
⎝
⎠T ⎝
⎠T
⎝
⎠T ⎝
⎠T
⎛∂ µ ⎞ ⎛∂ µ ⎞
⎜ ∂T ∂p ⎟ − ⎜ ∂T ∂p ⎟
V ∆αV ∆αV ⎝
=−
=
= 2 ( II ) ⎠ ⎝ 2 ( I ) ⎠
−V ∆k
∆k
⎛∂ µ ⎞ ⎛∂ µ ⎞
⎜ ∂p 2 ⎟ − ⎜ ∂p 2 ⎟
⎝
⎠ ⎝
⎠
2
( II )
2
(I )
(3)
Объединяя обе формы, получаем для скачка {∆cp} в точке фазового перехода второго рода:
( ∆αV ) TV
∆αV
1
×
=
; ∆c p =
T V ∆αV
∆k
∆k
∆c p
2
(4)
Соотношения (2) - (4) называются уравнениями Эренфеста для фазовых переходов
второго рода.
Обсуждение возражения Юсти и Лауэ.
Лекция 8
11