Анализ фазовых превращений в двухкомпонентных сплавах

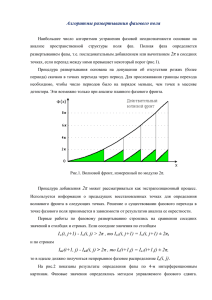
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
им. Р.Е. АЛЕКСЕЕВА»
Кафедра «Материаловедение, технологии материалов
и термическая обработка металлов»
АНАЛИЗ ФАЗОВЫХ ПРЕВРАЩЕНИЙ
В ДВУХКОМПОНЕНТНЫХ СПЛАВАХ
Методические указания к практическим занятиям
по дисциплине «Теория строения материалов»
для студентов всех специальностей
всех форм обучения
Нижний Новгород 2014
Составители: Сорокин В.К., Беляев Е.С., Воскресенская Т.А., Романов А.С.
УДК 621.002.3
Анализ фазовых превращений в двухкомпонентных сплавах: метод.
указания к практическим занятиям для студентов всех специальностей
всех форм обучения/ НГТУ; сост.: Сорокин В.К., Беляев Е.С., Воскресенская Т.А., Романов А.С. - Н.Новгород, 2014.- 30 с.
Научный редактор С.В. Костромин
Редактор Э.Б. Абросимова
Подп. в печ. 14.07.14. Формат 60х84 1/16. Бумага газетная. Печать офсетная. Печ.л. 1,9 Уч.-изд.л. 1,1. Тираж 300 экз. Заказ
Нижегородский государственный технический университет им. Р.Е. Алексеева.
Типография НГТУ. 603950, Н.Новгород, ул. Минина, 24.
© Нижегородский государственный
технический университет, 2014
1. Общие сведения
Анализ фазовых превращений в металлических сплавах проводится
в следующем порядке:
1) начертить диаграмму фазового равновесия заданной системы,
обозначить буквами характерные течки и указать фазы во всех фазовых
областях;
2) описать, к какому типу относится диаграмма фазового равновесия
и указать трёхфазные превращения, имеющие место в системе;
3) подсчитать число степеней свободы во всех фазовых областях для
заданного сплава X;
4) по указанию преподавателя определить темп кристаллизации для
сплава X;
5) начертить кривую охлаждения сплава Х с учётом темпа кристаллизации в интервале между температурами ликвидуса и солидуса;
6) подчитать по правилу отрезков массы равновесных фаз и массы
структурных составляющих при комнатной температуре, исходя из 100 кг
первоначального расплава;
7) записать все фазовые превращения при охлаждении сплава Х;
8) зарисовать схемы изменения микроструктуры для сплава Х при
охлаждении до комнатной температуры.
Для понимания фазовых превращений необходимо знание основных
представлений, используемых при анализе диаграмм состояния.
Простые и сложные вещества, выделенные из окружающего мира
реально существующими или воображаемыми поверхностями, называют
термодинамической системой. Система характеризуется рядом присущих
ей термодинамических параметров: температурой, давлением, концентрацией и др. Совокупность параметров определяет состояние системы. Система может быть гомогенной (однородной), если состав и свойства однаковы во всех точках, и гетерогенной (неоднородной), если она состоит из
нескольких фаз. Под фазой поиимают совокупность материальных частей
системы, обладающих одинаковым или непрерывно от точки к точке изменяющимися термодинамическими параметрами. Фазы отделены одна от
другой поверхностями раздела, где параметры изменяются скачком.
Такое состояние системы, при которое все термодинамические параметры имеют определенные значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго, называется равновесным.
Система самопроизвольно переходит в состояние равновесия при неизменных внешних условиях. Установление равновесного состояния системы произойдет, когда свободная энергия системы достигнет минимального значения (рис. 1).
3
Вещества, минимально необходимые для составления данной системы, называются компонентами. При определенных условиях разные фазы
одного и того же вещества могут находиться в равновесии друг с другом,
соприкасаясь между собой. Равновесие фаз имеет место лишь при определенных значениях параметров системы. Число термодинамических параметров системы, которые могут изменяться независимо друг от друга без
нарушения равновесия фаз и изменения числа фаз, называется числом
степеней свободы системы или ее вариантностью. Между числом компонентов К, числом равровесных фаз Ф и вариантностью системы С существует аналитическая зависимость, называемая правилом фаз Гиббса. При
постоянном давлении С = К – Ф + 1, т.е. число степеней свободы равно
разности между числом компонентов и числом фаз плюс один.
Рис.1
Переход из одной фазы в другую, которые характеризуются изменением объёма и тепловыми эффектами, называются фазовыми переходами
I-го рода. К ним относятся превращения твёрдого тела в жидкость, жидкости в пар и т.д. Состояние каждой фазы в системе, состоящей из двух
компонентов, может быть изображена геометрически точкой на плоскости, координатами которой служат температура и концентрация (рис. 2).
За концентрацию принимается отношение массы одного из компонентов в
данной фазе к массе всей фазы. Прямая АВ, отложенная на оси абсцисс,
характеризует концентрацию компонентов от 0 до 100%. Конечные точки
А и В соответствуют компонентам.
Графически выраженная, зависимость Т-х между значениями переменных, определяющих состояние системы (температура, концентрация),
представляет собой диаграмму состояния системы или диаграмму фазового равновесия. Каждая точка в системе координат Т-х соответствует определенному состоянию системы и называется фигуративной. Процесс нагревания или охлаждения сплава графически изображается перемещением
точки, соответствующей данному сплаву, вверх или вниз по вертикали.
4
Переход сплава из одного состояния в другое отмечается точками, а совокупность таких точек даёт линии, разделяющие диаграмму состояния на
отдельные поля (области). Каждая область диаграммы охватывает все
возможные сочетания температур и концентраций, отвечающих равновесному существованию определённой фазы или фаз.
Рис. 2
2. Анализ фазовых превращений в двойных сплавах с неограниченной растворимостью компонентов в жидком и твёрдом состояниях
Диаграмма фазового равновесия для рассматриваемого случая представлена на рис. 3.
Рис. 3
5
Как видно, в диаграмме фазового равновесия наблюдается три области состояний: область гомогенного жидкого раствора «Ж» выше линии
МСО, область гомогенного твёрдого раствора, обозначенного греческой
буквой α, ниже линии МКО и область двухфазного раствора «Ж + α» между линиями МСО и МКО.
Линия МСО представляет собой геометрическое место точек температур начала кристаллизации (или конца плавления) твёрдой фазы α и называется линией ликвидус. Геометрическое место точек температур конца
кристаллизации (или начала плавления) твёрдой фазы есть линия МКО,
называемая линией солидус.
Выше линии ликвидус жидкий раствор является ненасыщенным, т.е.
в нём ещё может раствориться добавочное количество компонентов. На
линии ликвидус жидкий раствор становится насыщенным, т.е. таким, в
котором компонент при данной температуре уже в большем количестве не
растворяется. Ниже линии ликвидус сплавы переходят в двухфазную область «жидкий раствор + твёрдый раствор». Следовательно, линия ликвидус представляет собой геометрическое место точек концентраций жидкого раствора, находящегося в равновесии с твёрдым раствором.
Аналогично линия солидус характеризует концентрацию твёрдого
раствора, находящегося в равновесии с жидким раствором. Ниже линии
солидус МКО находится область ненасыщенного твёрдого раствора.
Так, для сплава Х1 при температуре Т3 фигуративной точке 3 системы отвечают на горизонтальной линии фигуративной точке 4 (солидус) и
5 (ликвидус), находящихся в равновесии соответственно твёрдой фазы α и
жидкой фазы Ж. Следовательно, концентрация твёрдой фазы выражается
точкой 4, а равновесной с ней жидкой фазы – точкой 5.
Фигуративные точки, выражающие концентрации двух равновесных
фаз, называются сопряжёнными точками, а кривые, образованные рядами
этих точек, называются сопряжёнными кривыми. Изотермы, соединяющие фигуративные точки двух фаз, находящихся в равновесии (т.е. сопряжённые точки), называются конодами. Для рассмотренного примера
конодой будет линия 4-5. Следовательно, при температурах Т1 и Т2 конодами будут линии 1’-1 и 2-2’.
Соотношение количеств находящихся в равновесии фаз определяется правилом отрезков (или рычага):
QЖ 4 − 3
=
,
Qα 3 − 5
т.е. массы фаз, находящиеся в соотношении, обратно пропорциональны
отрезкам, на которые фигуративная точка 3 делит изотерму (коноду), соединяющую сопряжённые точки 4 и 5.
6
Массу каждой отдельно взятой фазы можно определить из следующих соотношений:
4−3
3−5
QЖ =
100%, Qα =
100%,
4−5
4−5
т.е. для определения количества жидкой фазы необходимо взять отношение длины отрезка 4-3, примыкающего к области твёрдой фазы, к длине
коноды 4-5; для подсчёта твёрдой фазы берётся отношение длины отрезка
3-5, примыкающего к области жидкой фазы к длине коноды 4-5.
Рассмотрим фазовые превращения, происходящие в рассматриваемой системе, на примере охлаждения сплава состава Х1. Выше точки 1
сплав находился в области однофазного ненасыщенного жидкого
раствоpa. Применяя правило фаз, будем иметь для однофазной области
«Ж» число степеней свободы:
СЖ = К – Ф + 1 = 2 – 1 + 1 = 2.
Так как С = 2, то возможно в пределах области жидкой фазы, выше
линии ликвидус МСК, изменять произвольно по нашему выбору, одновременно температуру и концентрацию, не нарушая равновесного однофазного состояния системы. Геометрически это означает, что фигуративная точка может быть смещена в любом направлении в области выше линии ликвидус МСК.
В интервале температур Т1-Т2 сплав находится в двухфазной области
«жидкий раствор + твердый раствор» и число степеней свободы по правилу фаз равно:
СЖ+α = К – Ф + 1 = 2 – 2 + 1 = 1.
При С = 1 допустимо произвольно изменять только один параметр
состояния: температуру или концентрацию одного из компонентов. Геометрически это значит, что фигуративная точка в области между МСО и
МКО может быть смещена или по вертикали (шкала температур) без изменения состава сплава, или по изотерме, когда изменяется состав сплава
при постоянной температуре. Каждой температуре отвечает новая, строго
определенная концентрация жидкой и находящейся с ней в равновесии
твердой фазы.
При температуре ниже точки 2 сплав находится в области однофазного ненасыщенного твердого раствора и число степеней свободы:
Сα = К – Ф + 1 = 2 – 1 + 1 = 2.
Следовательно, возможно одновременно изменять температуру и концентрацию, сохраняя равновесное состояние системы.
Далее построим кривую охлаждения сплава состава Х1. В соответствии с правилом фаз кристаллизация твердого раствора происходит в некотором интервале температур T1-Т2, называемой интервалом кристаллизации (С = К – Ф + 1 = 2 – 2 +1 = 1), и на кривой охлаждения будут две критических точки 1 и 2 (см. рис. 3). Ход кривой охлаждения в интервале
7
температур между точками ликвидуса 1 и солидуса 2 зависит от темпа
(интенсивности) кристаллизации. Темп кристаллизации характеризует
увеличение в сплаве количества кристаллов при понижении температуры,
т.е. скорость кристаллизации по температуре (производная массы по температуре dM/dT). Для сплавов различного химического состава при понижении температуры на одинаковую долю интервала кристаллизации (например, на 1/2 этого интервала) кристаллизуется различное количество
всей массы сплава и характер кривых охлаждения будет различен.
Так, для сплава X1 количество твердой фазы при Т3 (1-3 = 3-2) определяется по правилу отрезков следующим отношением:
3−5
Qα =
100% > 50%.
4−5
В этом сплаве в начальной стадии кристаллизации приращение массы твердой фазы изменяется с понижением температуры очень значительно, поэтому на кривой охлаждения четко выявляется точка ликвидуса
1; в интервале температур Т1-Т2 кривая охлаждения является выпуклой
(рис. 3).
У сплава Х2 количество твердой фазы при T6 (9-6 = 6-10):
6−8
Qα =
100% < 50%.
7 −8
Приращение массы в начальный период кристаллизации незначительное, точка ликвидус 9 выявляется нечетко и кривая охлаждения в интервале температур Т4-Т5 является вогнутой.
После построения кривой охлаждения рассмотрим процессы, происходящие при охлаждении сплава состава X1. Выше температуры ликвидуса T1 сплав находится в области однофазного ненасыщенного жидкого
раствора. При T1 жидкий раствор становится насыщенным.
Ниже T1 начинается фазовый переход жидкой фазы в твердую (твердый раствор), который заканчивается при температуре солидуса T2. Концентрация жидкой и твердой фазы изменяется при этом по сопряженным
кривым 1-2’ и 1’-2, соответственно. Следовательно, концентрация жидкой
фазы меняется по отрезку 1-2’ кривой ликвидуса, а твердой фазы – по отрезку 1’-2 кривой солидуса.
Процесс фазового перехода записывают следующим образом:
−Т
Ж 1− 2 ' Т

→ α 1 ' −2 .
В левой части записывается исходная фаза, а в правой – конечная.
Стрелка означает фазовый переход, a T1 и Т2 над стрелкой – температуры
начала и конца фазового перехода, а индексы 1’-2 фазы в левой части показывают изменение концентрации исходной фазы в интервале температур Т1 – Т2 фазового перехода, а индексы 1’-2 фазы α в правой части – соответственно изменение концентрации конечной фазы.
1
2
8
Представленная запись читается так: жидкая фаза в интервале температур Т1-Т2 переходит в твёрдую фазу α, причём концентрация жидкой
фазы изменяется по линии 1-2’, а твёрдой фазы – по линии 1’-2.
Ниже температуры солидуса Т2 происходит охлаждение однофазного
ненасыщенного твёрдого раствора. Аналогично анализируется процесс
фазового перехода и для сплава состава Х2.
3. Анализ фазовых превращений в двойных сплавах с полной
растворимостью компонентов в жидком состоянии и ограниченной
растворимостью в твёрдом состоянии
Такие диаграммы фазового равновесия являются наиболее распространенными. Они подразделяются на системы с перитектическим и эвтектическим превращениями.
Диаграмма фазового равновесия с ограниченной растворимостью
компонентов в твердом состоянии и наличием перитектическсго превращения представлена на рис. 4.
Как видно, на диаграмме фазового равновесия имеется три однофазных области и три двухфазных области. Выше линии ликвидус СРК –
расположена область ненасыщенного жидкого раствора Ж. Ниже линии
СМ (солидус) находится область твердого раствора компонента В в компоненте А, обозначенного буквой α; растворимость В в А ограничена линией МА, называемой линией предельной растворимости (пли линией
насыщения).
Рис. 4
9
Ниже линии ОК (солидус) расположена область твердого раствора
компонента А в компоненте В, обозначенного буквой β. Предельная растворимость этого твердого раствора ограничена линией ОВ.
При температуре ТМОР происходит перитектическое превращение:
Ж Р + α М Т
→ β О ,
т.е. жидкая фаза концентрации точки перитектики Р взаимодействует
(реагирует) с ранее образовавшимся твёрдым раствором α, концентрации
точки М; в результате этой реакции образуются новые кристаллы твёрдого
раствора β концентраций точки О. Характерной особенностью перитектического превращения является то, что жидкая фаза находится в равновесии с двумя твёрдыми фазами, которые обогащены одним и тем же компонентом по сравнению с жидкой фазой.
В соответствии с правилом фаз при трёхфазном равновесии в двухкомпонентной системе число степеней свободы равно нулю:
С = К – Ф + 1 = 2 – 3 + 1 = 0.
Следовательно, в случае трёхфазного равновесия температура и концентрация фаз не могут меняться; на кривой охлаждения будет наблюдаться горизонтальная температурная остановка. Горизонтальная изотермическая линия МОР на диаграмме, фазового равновесия является фазовой областью при постоянной температуре перитектического превращения, на которой в равновесии находится три фазы: Ж; α; β. Линия МОР
одновременно является и линией солидус. Рассмотрим фазовые превращения, происходящие при охлаждении в рассматриваемой системе, на
примере сплавов составов Х1, Х2, Х3.
Сначала рассмотрим сплав Х2. Схема превращений запишется следующим образом:
−Т
Ж 3− Р Т

→ α 3' − М ;
Т
Ж Р + α М →
βО .
В этом сплаве соотношение количеств жидкой фазы и твёрдой фазы
α в начале перитектического превращения (точка 4 на диаграмме фазового
равновесия) равно:
QЖ МО
=
.
Qα
ОР
Такое соотношение точно соответствует полному перитектическому
превращению в твёрдый раствор β, поэтому ниже Т4 сплав находится в
однофазной области ненасыщенного β-твердого раствора.
Для сплава X1 в начале перитектического превращения (точка 2)
имеем:
QЖ М − 2 МО
=
<
,
Qα
2 − Р ОР
МОР
3
4
4
10
т.е. жидкая фаза исчезает раньше, чем прореагируют все кристаллы твёрдой фазы α, Схема превращений будет следующая:
−Т
Ж 1− Р Т

→ α1' − М ;
Т
Ж Р + α М → β О + α М (избыток ).
Ниже температуры Т2 сплав X1 находится в двухфазной области.
В сплаве Х3 соотношение жидкой и твёрдой фаз в начале перитектического превращения (точка 6) выражается соотношением:
QЖ 6 − М МО
=
,
>
Qα 6 − Р ОР
следовательно, в конце перитектического превращения в избытке остается
жидкая фаза, которая при дальнейшем охлаждении в интервале температур T6 – Т7 переходит в твердый раствор β. Для сплава Х3 будут наблюдаться следующие фазовые переходы:
−Т
Ж 5− Р Т

→ α 5'− М ;
Т
Ж Р + α М →
β О + Ж Р (избыток );
−Т
Ж Р −7 ' Т

→ β О −7 .
Диаграмма фазового равновесия с ограниченной растворимостью
компонентов в твёрдом состоянии и наличием эвтектического превращения дана на рис. 5.
Выше линии ликвидус АЕВ находится однофазная область ненасыщенного жидкого раствора. Ниже линии AM (солидус) расположена однофазная область твёрдого раствора α, которая ограничена линией предельной растворимости МО.
Ниже линии ВК (солидус) находится однофазная область твёрдого
раствора β, ограниченная линией предельной растворимости КС.
1
2
5
6
2
6
6
7
Рис. 5
11
При температуре ТМЕК происходит эвтектическое превращение:
Ж Е Т
→ α М + β К ,
т.е. жидкая фаза концентрации эвтектической точки Е кристаллизуется с
образованием двух твёрдых фаз: твёрдого раствора α концентрации точки
М, и твёрдого раствора β концентрации точки К. Характерной особенностью эвтектического превращения является то, что жидкая фаза находится
в равновесии с двумя твёрдыми фазами, одна из которых обогащена по
сравнению с жидкой фазой первым компонентом, а вторая обогащена другим компонентом.
По правилу фаз при трёхфазном равновесии число степеней свободы
равно нулю:
С = К – Ф + 1 =2 – 3 + 1 = 0,
т.е. температура и концентрация фаз в течение всего превращения остаются постоянными.
На диаграмме фазового равновесия изотермическая линия МЕК является трёхфазной областью, на которой в равновесии находятся фазы α и
β. Эта линия одновременно является линией солидус.
Рассмотрим процессы фазовых переходов при охлаждении сплавов
Х1, Х2, Х3.
В сплаве Х3 эвтектического состава при Т6 происходит эвтектическое
превращение:
Т
Ж Е →
α М + βК .
При температуре ниже T6 в связи с изменением предельной растворимости компонентов в твёрдых растворах α и β происходят одновременно следующие фазовые переходы:
Т
→ β КС ;
α МО Т−

Т −Т
β КС → α МО ;
где ТК – комнатная температура.
В сплаве Х2 идут следующие превращения:
−Т
Ж 4− Е Т

→ α 4'− М .
Соотношение количества жидкой и твёрдой фаз в конце кристаллизации твёрдого раствора α (температура Т5) определяется следующим образом:
QЖ 5 − М
=
.
Qα 5 − Е
Количество жидкой фазы соответственно равно:
5−M
QЖ =
.
М −E
Эта жидкая фаза концентрации эвтектической точки Е при Т5 превращается в смесь двух твёрдых растворов:
МЕК
6
О
К
6
К
4
5
12
Т
Ж Е →
α М + βК .
В связи с уменьшением растворимости компонентов в твёрдых растворах ниже Т5 идут следующие фазовые превращения:
Т
→ β КС ;
α МО Т−

Т −Т
β КС → α МО .
Фазовые переходы для сплава Х1, даны ниже:
−Т
Ж 1− 2 ' Т

→ α 1 ' −2 ;
Т −Т
α 3−О → β 3 ' − С ;

Т −Т
β 3 ' − С → α 3−О .
Диаграммы фазового равновесия, представляя собой совокупность
областей устойчивости и равновесия фаз, характеризуют фазовое состояние сплавов в равновесных условиях. В диаграммах фазового равновесия
не учитываются размеры, форма и взаимная ориентировка отдельных фаз,
поэтому детальные сведения о микроструктуре сплавов в равновесном состоянии из диаграммы состояния получить невозможно. Качественная характеристика ожидаемой микроструктуры в условиях, близких к равновесным, может быть дана по диаграмме фазового равновесия, исходя из
последовательных фазовых переходов при охлаждении и нагреве сплавов.
Подробные сведения о микроструктуре возможно получить только
на основании микроструктурного анализа сплавов с помощью металлографического микроскопа. Микроструктура сплавов для случая ограниченной растворимости компонентов в твёрдом состоянии с наличием эвтектического превращения представлена на рис. 6.
Как видно, микроструктура сплава Х1 состоит из зёрен твёрдого раствора α и избыточных (вторичных) кристаллов твёрдого раствора β. Сплава Х2 имеет микроструктуру из кристаллов твёрдого раствора α и эвтектики α+β. Эвтектика представляет собой смесь двух твёрдых фаз и имеет
пластинчатое, зернистое или скелетное строение. Эвтектика образуется в
результате эвтектического превращения:
Ж Е Т
→ α М + β К .
5
К
5
5
К
1
2
3
К
3
К
МЕК
Рис. 6
Сплав Х3, называемый эвтектическим, имеет микроструктуру эвтектики. В сплаве Х4 наблюдается структура из кристаллов твёрдого раствора
13
β и эвтектики, в сплаве Х5 – из зёрен твёрдого раствора β и избыточных
(вторичных) кристаллов твёрдого раствора α. Микроструктура сплава Х6
состоит из зёрен твёрдого раствора β.
Отдельные структурно обособленные части (элементы) микроструктуры сплавов, которые при рассмотрении под микроскопом имеют своё
характерное строение, называются структурными составляющими сплавов. Так, в сплаве Х2 структурными составляющими являются кристаллы
твёрдого раствора α и эвтектика, в сплаве Х3 – одна структурная составляющая (эвтектика).
В ряде случаев данные о структурных составляющих, полученные
путем микроструктурного анализа, указываются на диаграмме фазового
равновесия в виде структурных областей, разделенных пунктирными вертикальными линиями. Диаграмма фазового равновесия с обозначением
структурных областей по данным микроструктурного анализа приведена
на рис. 7, а. Сплавы, находящиеся по составу между точками М и Е, называются доэвтектическими, а между Е и К – заэвтектическими.
Количество структурных составляющих в сплавах можно подсчитать
по правилу отрезков. Так, в сплаве Х2 (см. рис. 7) количество эвтектики
равно:
5−M
QЭВТ =
100% ,
М −E
а количество второй структурной составляющей – кристаллов твёрдого
раствора α определяется из следующего соотношения:
5− Е
100% .
Qα =
М −E
Данные об изменении количества структурных составляющих в зависимости от химического состава сплава при заданной температуре иногда представляют в виде структурной диаграммы (рис. 7, б).
4. Анализ фазовых превращений в двойных сплавах с ограниченной растворимостью компонентов в жидком и твёрдом состояниях
Диаграмма фазового равновесия для рассматриваемого случая приведена на рис. 8.
Выше линии NEBKMR сплавы находятся в области однородной жидкой фазы. В области KmBMnK сплавы состоят из двух жидких фаз Ж’ и
Ж”, концентрация которых определяется линиями KmB и KnM. Кривая
BmKnM является линией предельного насыщения, или линией расслаивания.
При температуре BMC происходит монотектическое превращение:
Ж М Т
→ Ж В + β С ,
ВМС
14
т.е. жидкая фаза концентрации точки М превращается в смесь жидкой фазы концентрации точки В и твёрдой фазы β концентрации точки С.
Рис. 7
Рис. 8
По правилу фаз в случае монотектического превращения число степеней свободы равно нулю:
С = К – Ф + 1 = 2 – 3 + 1 = 0,
т.е. температура и концентрации фаз в течение всего превращения остаются неизменными.
15
Рассмотри процессы фазовых переходов при охлаждении сплава состава X1. В интервале температур T1-Т2 из однородной жидкой фазы выделяется жидкая фаза Ж’, концентрация которой изменяется по линии 1’-В.
Концентрация жидкой фазы Ж” изменяется по линии 1-М:
−Т
Ж 1"− М Т

→ Ж 1' ' − В .
При температуре Т2 происходит монотектическое превращение:
Т
Ж "М →
Ж 'В + β С .
В интервале температур Т2-Т3 происходит кристаллизация твёрдого
раствора:
−Т
Ж В − Е Т

→ β СD .
При Т3 происходит эвтектическое превращение:
Т
Ж Е →
α А + βD .
Ниже Т3 идут следующие превращения:
Т
→ β DT ;
α АК Т−

Т
→ α AK .
β DT Т−
1
2
2
2
3
3
К
3
1
К
3
1
5. Анализ фазовых превращений в двойных сплавах с наличием
химического соединения
Два компонента могут вступать в химическое взаимодействие друг с
другом, образуя химическое соединение. Если химическое соединение устойчиво при всех температурах до температуры его плавления, то такое
соединение называется конгруэнтно плавящимся.
Диаграмма фазового равновесия для этого случая с образованием
твёрдых растворов α и β на основе компонентов и твёрдого раствора γ на
основе химического соединения АmBn представлена на рис. 9.
Для сплава состава Х2 концентрации компонентов в системе соответствуют химическому соединению. Максимум на кривой ликвидус для
сплава Х2 может быть острым при малой склонности химического соединения к диссоциации АmBn ↔ mA + nB вблизи температуры плавления или
пологим при большой степени диссоциации.
Устойчивые химические соединения ведут себя как компоненты, и
диаграмма фазового равновесия может рассматриваться как составленная
из двух диаграмм с наличием следующих эвтектических превращений:
Т
Ж Е 
→ α М + γ С ;
МЕ1С
1
Ж Е 
→ γ F + β D .
В качестве примера ниже дана схема фазовых переходов для сплава
состава Х1:
−Т
Ж 1− Е Т

→ γ 1' − С ;
Т FE 2 D
2
1
2
1
16
Т
Ж Е →
αМ + γС ;
2
1
α М − А → γ С − В ;
Т
γ С − В Т−
→ αМ −А .
Т 2 −Т К
К
2
Рис. 9
В случае образования неустойчивого (инконгруэнтно плавящегося)
соединения и ограниченной растворимости в твёрдом состоянии диаграмма фазового равновесия имеет вид, представленный на рис. 10. Твёрдый
раствор γ на основе химического соединения АmBn при нагреве устойчив
только до температуры ТРОМ, при которой происходит распад:
γ О Т
→ Ж Р + β М .
При охлаждении твёрдый раствор γ образуется в результате перитектического превращения:
Ж Р + β М Т
→ γ О .
Ниже рассмотрены фазовые переходы при охлаждении сплава состава Х1:
−Т

→ β1 ' − М ;
Ж 1− Р Т
Т
Ж Р + β М →
γО ;
−Т
Ж Р − Е Т

→ γ ОК ;
Т
αМ + γК ;
Ж Е →
Т
→ γ К −В ;
α МА Т−

Т −Т
γ К − В → α М − А .
РОМ
РОМ
1
2
2
2
3
3
3
3
К
К
17
Рис. 10
6. Анализ фазовых превращений в двойных сплавах при
наличии полиморфных превращений у отдельных компонентов и в
случаях перитектоидного и эвтектоидного превращений
Некоторые металлы обладают полиморфизмом, т.е. способностью
находиться в различных модификациях, отличающихся строением кристаллической решетки. Каждая кристаллическая модификация устойчива
в определенной температурной области. Наличие полиморфизма у отдельных компонентов отражается на диаграммах фазового равновесия. На рис.
11 показана одна из возможных диаграмм фазового равновесия для случая
растворимости в твёрдом состоянии при наличии полиморфных превращений у одного из компонентов при температурах ТМ и ТС.
Рассмотрим фазовые переходы, происходящие при охлаждении
сплава состава X1. Кристаллизация твёрдого раствора γ происходит в интервале температур Т1 и Т2:
−Т
Ж 1−2 ' Т

→ γ 1 ' −2 .
В интервале температур Т3-Т4 происходит фазовый переход (перекристаллизация в твёрдом состоянии) твёрдого раствора γ на основе одной
из модификаций компонента в твёрдый раствор β на основе другой модификации компонента:
−Т
γ 3− 4 Т

→ β 3 ' −4 .
Аналогичная фазовая перекристаллизация происходит в интервале
температур Т5-Т6:
−Т
β 5−6 ' Т

→ α 5 ' −6 .
1
2
3
4
5
6
18
Рис. 11
В некоторых системах в твёрдом состоянии происходят перитектоидные и эвтектоидные превращения. На рис. 12 представлена диаграмма
фазового равновесия с наличием перитектического превращения при температуре ТРМС, т.е. твёрдая фаза γ концентрации точки перитектики Р
взаимодействует с твёрдой фазой β концентрации точки С, образуя новую
твёрдую фазу α концентрации точки М.
Рис. 12
Рассмотрим фазовые превращения при охлаждении сплава Х1:
−Т
Ж 1− Е Т

→ γ 1' − А ;
Т
Ж Е → γ А + β В ;
1
2
2
19
−Т

→ β В −С ;
γ А− Р Т

Т −Т
→ γ А− Р ;
β В −С 
Т
γ Р + β С →
αМ ;
Т −Т
γ Р − 4 ' 
→ α М − 4 .
На рис. 13 показана одна из возможных диаграмм фазового равновесия с наличием эвтектоидного превращения при температуре ТАЕС:
β Е Т→
 α А + γС ,
т.е. твёрдая фаза β концентрации точки Е превращается в смесь, состоящую из кристаллов α и γ твёрдых фаз.
2
3
2
3
3
3
4
АЕС
Рис. 13
Рассмотрим фазовые превращения на примере сплава Х1:
−Т

→ α 1' − В ;
Ж 1− Р Т
Т
Ж Р + α В →
βК ;
Т −Т
→ β К −3 ;
Ж Р −3 ' 
Т
β Е → α А + γ С .
1
2
2
2
3
Е
7. Анализ фазовых превращений в железоуглеродистых сплавах
В качестве примера реальной диаграммы состояния рассмотрим диаграмму фазового равновесия системы железо-углерод. Реально существуют стабильная диаграмма состояния железо-графит при очень малых
скоростях охлаждения и метастабильная диаграмма состояния железокарбид железа Fe3C (цементит) при повышенных скоростях охлаждения.
Стабильная диаграмма фазового равновесия железо-графит приведена на рис. 14. Она относится к случаю ограниченной растворимости угле20
рода в железе, имеющем полиморфные модификации, с наличием эвтектического превращения:
Ж С' t
→ γ E' + Г F' ,
перитектического превращения:
t
Ж B + δ H →
γJ
и эвтектоидного превращения:
γ S' t
→ α Р' + Г К' .
Рассмотрим фазовые переходы при охлаждении сплава Х1:
−t
Ж 1−С ' t→

γ 1' − E ' ;
t
Ж С' → γ E' + Г F' (графит ) ;
−t
γ Е' − S' t→

Г F' − K' ;
t
γ S' 
→ α P' + Г K' ;
−t
α P' − Q' t

→ Г K' .
E' C' F'
HJB
P' S' K'
1
2
2
2
3
3
3
K
Рис. 14
Meтастабильная диаграмма состояния железо-карбид железа представлена на рис. 15.
В этой системе наблюдаются следующие трехфазные превращения:
t
- перитектическое:
Ж B + δ H →
γJ ;
t
- эвтектическое:
Ж С → γ E + Fe3 C F ;
- эвтектоидное:
γ S t→ α Р + Fe 3 C К .
Фазовые переходы при охлаждении сплава Х1 приведены ниже:
−t
Ж 1− 2 ' t→

γ 1 ' −2 ;
t
γ S →
α Р + Fe3 C К ;
−t
α PQ t

→ Fe3 C K .
HJB
ECF
PSK
1
2
4
4
K
21
Рис. 15
Метастабильная диаграмма состоянии железо-карбид железа с обозначением структурных областей по данным микроструктурного анализа
представлена на рис. 16, а. Структурные диаграммы для стали и чугунов
приведены на рис. 16, б и в.
Фазы и структурные составляющие на диаграмме состояния и структурных диаграммах указаны в соответствии с общепринятыми интернациональными наименованиями:
- твёрдый раствор α (δ) – феррит Ф;
- твёрдый раствор γ – аустенит А;
- химическое соединение Fe3C – цементит Ц;
- эвтектика А + Ц – ледебурит Л;
- эвтектоид Ф + Ц – перлит П.
На рис. 16: доэвтектоидная сталь – феррит (светлые участки) и перлит (темные участки), ×500; эвтектоидная сталь – перлит, ×1000; заэвтектоидная сталь – перлит и цементит в виде сетки, ×2000; доэвтектический
чугун – перлит (темные участки) ледебурит и цементит вторичный, ×500;
эвтектический чугун – ледебурит (смесь аустенита и цементита), ×500; заэвтектический чугун – цементит (светлые пластины) и ледебурит, ×500.
22
Рис. 16
23
Список литературы
1. Материаловедение и технология материалов: учебник для машиностроительных специальностей вузов/ Г.П. Фетисов [и др.]; под ред. Г.П.
Фетисова. – 5-е изд.: стереотип. – М.: Высшая школа, 2007. – 862 с.
2. Материаловедение: учебник для вузов/ Б.Н. Арзамасов [и др.]; под общ.
ред. Б.Н. Арзамасова, Г.Г. Мухина. – 8-е изд., стереотип. – М.: Изд-во
МГТУ им. Баумана, 2008. – 648 с.
3. Готтштайн, Г. Физико-химические основы материаловедения: [пер. с
анг. К.Г. Зотовой, Д.О. Чаркина]/ Г. Готтштайн; под ред. В.П. Золотова. –
М.: БИНОМ. Лаборатория знаний, 2009. – 400 с.
4. Сорокин, В.К. Основы материаловедения и конструкционные материалы: учеб. пособие/ В.К. Сорокин. Нижний Новгород: Нижегород. гос.
техн. ун-т, 2006. – 226 с.
5. Захаров, А.М. Диаграммы состояния двойных и тройных систем/ А.М.
Захаров. – М.: Металлургия, 1954. – 356 с.
24
Приложение А
Задания по анализу фазовых превращений в двухкомпонентных
сплавах
Задания по анализу диаграмм состояний и фазовых превращений,
выдаваемые студентам, приведены в табл. П.А.1.
Таблица П.А.1. Задания по анализу диаграмм состояний и фазовых превращений
Номер задания
Система
Номер рисунка
1
железо-фосфор
П.А.1
2
медь-мышьяк
П.А.2
3
медь-лантан
П.А.3
4
алюминий-кальций
П.А.4
5
алюминий-никель
П.А.5
6
алюминий-цинк
П.А.6
7
висмут-свинец
П.А.7
8
медь-берилий
П.А.8
9
никель-сурьма
П.А.9
10
титан-марганец
П.А.10
11
титан-германий
П.А.11
12
титан-углерод
П.А.12
Конкретные составы сплавов для анализа фазовых превращений указываются преподавателем.
Рис. П.А.1
Рис. П.А.2
25
Рис. П.А.3
Рис. П.А.4
Рис. П.А.5
Рис. П.А.6
26
Рис. П.А.7
Рис. П.А.8
Рис. П.А.9
Рис. П.А.10
Рис. П.А.11
Рис. П.А.12
27
Приложение Б
Пример выполнения заданий по анализу фазовых превращений
в двухкомпонентных сплавах
Задание: выполнить анализ фазовых превращений в сплаве х = 30%
олова системы свинец-олово.
1) вычерчиваем диаграмму фазового равновесия свинец-олово
(рис. П.Б.1, а);
2) эта диаграмма состояния относится к случаю полной растворимости компонентов в жидком состоянии и ограниченной растворимости в
компонентов в твёрдом состоянии с наличием эвтектического превращения при tВЕМ:
Ж Е t→
 α В + βМ ;
3) подсчитаем число степеней свободы во всех областях:
С = К – Ф + 1;
СЖ = 2 – 1 + 1 = 2;
СЖ+α = 2 – 2 + 1 = 1;
С2 = 2 – 3 + 1 = 0;
Сα+β = 2 – 2 + 1 = 1;
ВЕМ
Рис. П.Б.1
4) определим темп кристаллизации:
6−8
17мм
Qα =
100% =
100% = 61% > 50% ;
7 −8
28мм
5) вычерчиваем кривую охлаждения сплава х (рис. П.Б.1, б);
28
6) подсчитаем массу равновесных фаз при комнатной температуре tК:
3− 4
10
QЭВТ =
100% = 100% = 23,8 кг;
4−5
42
3−5
32
Qα =
100% = 100% = 76,2 кг.
4−5
42
Кроме количества фаз или структурных составляющих, с помощью
правила отрезков можно определить составы фаз или концентрацию компонентов (Pb и Sn) в фазах. Сплав x в точке 6 имеет две фазы: жидкую и
твёрдую α. Чтобы определить концентрацию компонентов, левый и правый концы каноды (7, 6, 8) сносим на ось концентраций и обозначаем соответственно 7’ и 8’. Точка 7’ покажет концентрацию компонентов в
твёрдой фазе α, а именно количество олова Sn ≈ 11%, остальное – свинец
Pb = 100 – 11 = 89%. Точка 8’ покажет количество компонентов в жидкой
фазе: олово Sn ≈ 43%, свинец Pb = 100 – 43 = 57%.
7) запишем фазовые переходы:
−t
Ж 1− Е t→

α 1' − B ;
t
Ж Е →
α B + βM ;
1
2
2
−t
α BK t
→ β MN ;

t −t
→ α BK ;
β MN 
8) нарисуем схему охлаждаемой микроструктуры (рис. П.Б.1, в).
2
K
2
K
29
Содержание
1. Общие сведения .............................................................................................. 3
2. Анализ фазовых превращений в двойных сплавах с неограниченной
растворимостью компонентов в жидком и твёрдом состояниях .................. 5
3. Анализ фазовых превращений в двойных сплавах с полной
растворимостью компонентов в жидком состоянии и ограниченной
растворимостью в твёрдом состоянии ............................................................. 9
4. Анализ фазовых превращений в двойных сплавах с ограниченной
растворимостью компонентов в жидком и твёрдом состояниях ................ 14
5. Анализ фазовых превращений в двойных сплавах с наличием
химического соединения ................................................................................. 16
6. Анализ фазовых превращений в двойных сплавах при наличии
полиморфных превращений у отдельных компонентов и в случаях
перитектоидного и эвтектоидного превращений.......................................... 18
7. Анализ фазовых превращений в железоуглеродистых сплавах.............. 20
Список литературы .......................................................................................... 24
Приложение А................................................................................................... 25
Приложение Б ................................................................................................... 28
30