Решение заданий варианта 6402

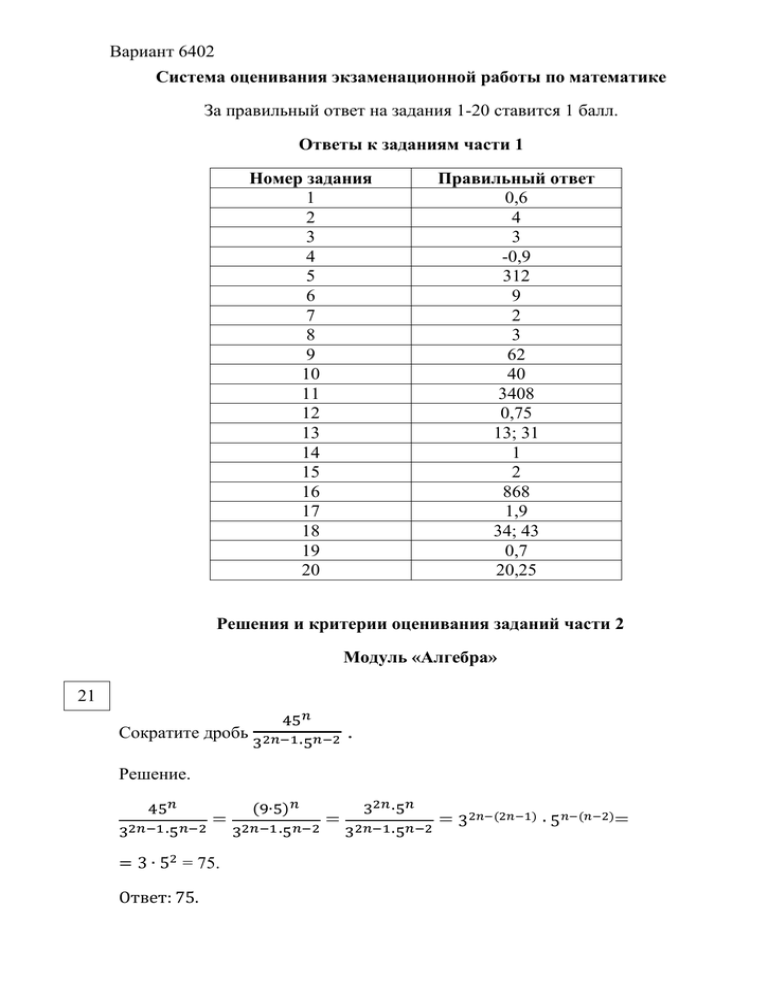
Вариант 6402
Система оценивания экзаменационной работы по математике
За правильный ответ на задания 1-20 ставится 1 балл.
Ответы к заданиям части 1
Номер задания
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Правильный ответ
0,6
4
3
-0,9
312
9
2
3
62
40
3408
0,75
13; 31
1
2
868
1,9
34; 43
0,7
20,25
Решения и критерии оценивания заданий части 2
Модуль «Алгебра»
21
Сократите дробь
45𝑛
32𝑛−1 ∙5𝑛−2
.
Решение.
45𝑛
32𝑛−1 ∙5𝑛−2
32𝑛 ∙5𝑛
= 32𝑛−1 ∙5𝑛−2 = 32𝑛−1 ∙5𝑛−2 = 32𝑛−(2𝑛−1) ∙ 5𝑛−(𝑛−2) =
= 3 ∙ 52 = 75.
Ответ: 75.
(9∙5)𝑛
Вариант 6402
Баллы
Критерии оценки выполнения задания
2
Правильно выполнены преобразования, получен верный ответ
1
Решение доведено до конца, но допущена ошибка вычислительного
характера или описка, с её учётом дальнейшие шаги выполнены
верно
0
Другие случаи, не соответствующие указанным выше критериям
2
Максимальный балл
22
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по
течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись
обратно через 7 часов от начала путешествия. На какое расстояние от
лагеря они отплыли, если скорость течения реки равна 3 км/ч, а
собственная скорость лодки 5 км/ч?
Решение.
Пусть искомое расстояние равно 𝑥 км. Скорость лодки при движении по
течению равна 8 км/ч, при движении против течения равна 2 км/ч. Время,
за которое лодка доплывёт от места отправления до места назначения и
𝑥
𝑥
обратно, равно ( + ) часа. Из условия задачи следует, что это время
8
2
𝑥
𝑥
равно 4 часам. Составим уравнение: ( + ) = 4.
8
2
Решив уравнение, получим 𝑥 = 6,4.
Ответ: 6,4 км.
Баллы
Критерии оценки выполнения задания
3
Правильно составлено уравнение, получен верный ответ
2
Правильно составлено уравнение, но при его решении допущена
вычислительная ошибка, с её учётом решение доведено до ответа
0
Другие случаи, не соответствующие указанным критериям
3
Максимальный балл
23
Постройте график функции
𝑦=
(𝑥−5)(𝑥2 −6𝑥+8)
𝑥−2
и определите, при
каких значениях m прямая y = m имеет с графиком ровно одну общую
точку.
Решение. Разложим числитель дроби на множители:
Вариант 6402
(𝑥 − 5)(𝑥 2 − 6𝑥 + 8)= (𝑥 − 5)(𝑥 − 2)(𝑥 − 4)
При 𝑥 ≠ 2 функция принимает вид:
𝑦 = (𝑥 − 5)(𝑥 − 4)=𝑥 2 − 9𝑥 + 20,
её график  парабола, из которой
выколота точка (2; 6).
Прямая 𝑦 = 𝑚 имеет с графиком ровно
одну общую точку либо тогда, когда
проходит через вершину параболы, либо
тогда, когда пересекает параболу в двух
точках, одна из которых  выколотая.
Вершина параболы имеет координаты
(4,5; −0,25).
Поэтому 𝑚 = −0,25 или 𝑚 = 6.
Ответ: 𝑚 = −0,25, 𝑚 = 6.
Баллы
Критерии оценки выполнения задания
4
График построен правильно, верно указаны все значения m, при
которых прямая 𝑦 = 𝑚 имеет с графиком ровно одну общую точку
3
График построен правильно, указаны не все верные значения m
0
Другие случаи, не соответствующие указанным выше критериям
4
Максимальный балл
Модуль «Геометрия»
24
В прямоугольном треугольнике ABC с прямым углом C известны катеты:
AC = 15, BC = 20. Найдите медиану CM этого треугольника.
Решение.
CM=
1
2
AB =
1
2
√𝐴𝐶 2 + 𝐵𝐶 2 =
1
= 2 √225 + 400= 12,5.
Ответ: 12,5.
Баллы
Критерии оценки выполнения задания
2
Получен верный обоснованный ответ
Вариант 6402
1
0
2
При верных рассуждениях допущена вычислительная ошибка,
возможно приведшая к неверному ответу
Другие случаи, не соответствующие указанным критериям
Максимальный балл
25
В параллелограмме KLMN точка B  середина стороны LM. Известно,
что BK = BN. Докажите, что данный параллелограмм  прямоугольник.
Доказательство. Треугольники KBL и NBM
равны по трём сторонам.
Значит, углы KBL и NBM равны. Так как их
сумма равна 180, то углы равны 90. Такой
параллелограммпрямоугольник.
Баллы
3
2
0
3
Критерии оценки выполнения задания
Доказательство верное, все шаги обоснованы
Доказательство в целом верное, но содержит неточности
Другие случаи, не соответствующие указанным критериям
Максимальный балл
26
Основание AC равнобедренного треугольника ABC равно 10. Окружность
радиуса 9 с центром вне этого треугольника касается продолжения
боковых сторон треугольника и касается основания AC в его середине.
Найдите радиус окружности, вписанной в треугольник ABC.
Решение.
Пусть O2  центр данной окружности,
а O1  центр окружности, вписанной
в треугольник ABC.
Вариант 6402
Точка касания K окружностей делит AC пополам.
Лучи AO2 и AO1  биссектрисы смежных углов, значит, угол O2AO1
прямой. Из прямоугольного треугольника O2AO1 получаем: AK2=
КO1KO2.
Следовательно,
𝐴𝐾2
O1 K = 𝑂
2𝐾
Ответ: 2
7
9
=
25
9
7
= 29.
.
Баллы
Критерии оценки выполнения задания
4
Ход решения верный, все его шаги выполнены правильно, получен
верный ответ
3
Ход решения верный, чертёж соответствует условию задачи, но
пропущены
существенные
объяснения
или
допущена
вычислительная ошибка
0
Другие случаи, не соответствующие указанным критериям
4
Максимальный балл