Упругопластический изгиб балки из линейно упрочняющегося

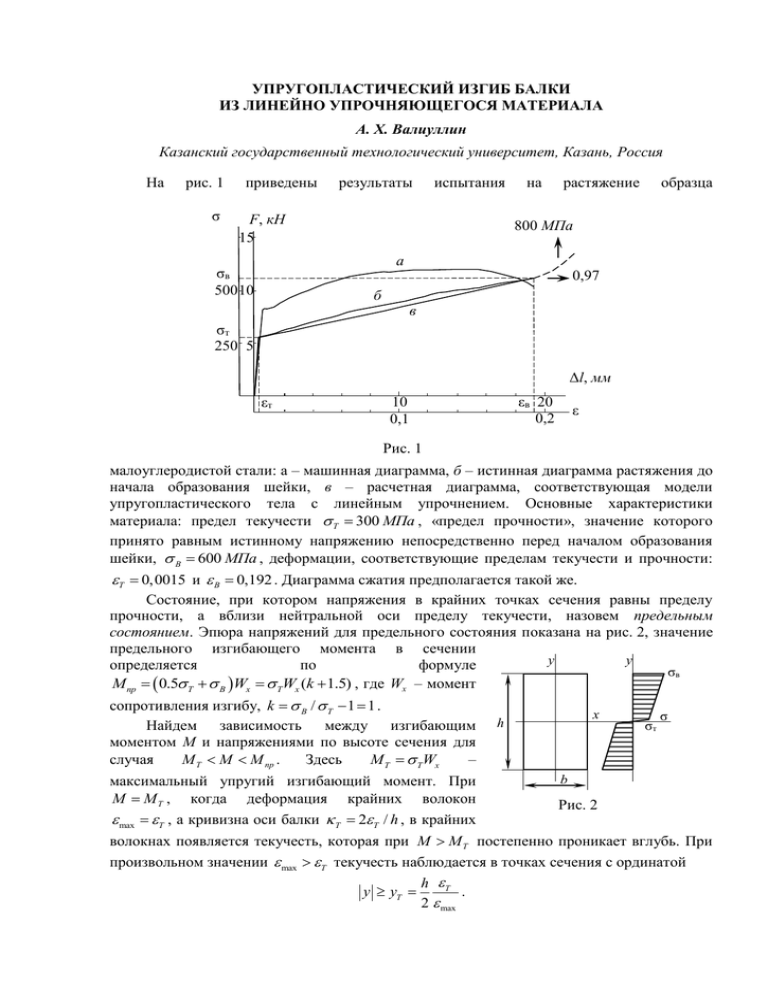
УПРУГОПЛАСТИЧЕСКИЙ ИЗГИБ БАЛКИ
ИЗ ЛИНЕЙНО УПРОЧНЯЮЩЕГОСЯ МАТЕРИАЛА
А. Х. Валиуллин
Казанский государственный технологический университет, Казань, Россия
На
рис. 1
σ
приведены
результаты
F, кН
15
испытания
на
растяжение
образца
800 МПа
а
σв
500 10
0,97
б
в
σт
250 5
Δl, мм
εт
10
0,1
εв 20
0,2
ε
Рис. 1
малоуглеродистой стали: а – машинная диаграмма, б – истинная диаграмма растяжения до
начала образования шейки, в – расчетная диаграмма, соответствующая модели
упругопластического тела с линейным упрочнением. Основные характеристики
материала: предел текучести  Т  300 МПа , «предел прочности», значение которого
принято равным истинному напряжению непосредственно перед началом образования
шейки,  В  600 МПа , деформации, соответствующие пределам текучести и прочности:
Т  0,0015 и  В  0,192 . Диаграмма сжатия предполагается такой же.
Состояние, при котором напряжения в крайних точках сечения равны пределу
прочности, а вблизи нейтральной оси пределу текучести, назовем предельным
состоянием. Эпюра напряжений для предельного состояния показана на рис. 2, значение
предельного изгибающего момента в сечении
y
y
определяется
по
формуле
σв
M пр   0.5 T   В Wx   TWx (k  1.5) , где Wx – момент
сопротивления изгибу, k   B /  T  1  1 .
x
σ
σт
Найдем зависимость между изгибающим h
моментом М и напряжениями по высоте сечения для
M T  M  M пр .
M T   TWx
случая
Здесь
–
b
максимальный упругий изгибающий момент. При
M  M T , когда деформация крайних волокон
Рис. 2
 max  T , а кривизна оси балки  T  2T / h , в крайних
волокнах появляется текучесть, которая при M  M T постепенно проникает вглубь. При
произвольном значении  max  T текучесть наблюдается в точках сечения с ординатой
h T
y  yT 
.
2  max
Принимая гипотезу плоских сечений и подставляя физические соотношения
Ey 2Ey max
, при y  yT ,
  E 


h
 T  2 y

  T  B
  max  T  , при y  yT
 B  T  h

в интегральную зависимость M    ydA , получим следующее уравнение (в безразмерном
A
виде):
2
3
 B  T  k  1   T   k max   T   E
1  

1 

m  1,5
   max    B  T    max    T
 B  T
где m  M /  TWx  .




3
 T 

  max ,
  max 
(1)
Из этого уравнения при известном значении m итерационным методом Ньютона
определяется значение  max , затем кривизна оси по формуле
  2 max / h
(2)
и – чисто геометрически, не прибегая к дифференциальному уравнению, находится
изогнутая ось балки.
Решены задачи чистого, поперечного и продольно-поперечного изгиба балки.
1. Чистый изгиб. В этом случае кривизна, определяемая формулой (2), постоянна,
поэтому решение сводится к построению дуги окружности радиусом   1/  и длиной,
равной длине балки. Выполнены расчеты при различных значениях момента и
относительной толщины балки.
2. Поперечный изгиб (рис. 3). В уравнении (2) безразмерный момент m заменяется
на m  z   2 fz / l , где f  F / FT , а FT  4 TWx / l .
Задача решается численно по такому
алгоритму. Задается значение угла поворота на
левом краю 0  01  02  / 2, где 01   / 2 и
02  0 – начало и конец возможного диапазона
изменения 0 ; задаются начальные значения
длины дуги изогнутой оси, абсциссы сечения,
Рис. 3
прогиба
и
угла
поворота:
s  0, z  0, w  0,   0 ; затем длине дуги дается приращение s и вычисляются новые
значения z , w : z  z  s  cos 0 , w  w  s  sin 0 . Здесь же определяется значение
m( z )  2 fz / l , после чего из уравнения (1) находится  max и кривизна – по формуле (2),
затем угол поворота в конце первого шага     s .
Так расчет продолжается до достижения середины балки. Проверяется условие
симметричности изогнутой оси: в середине балки угол поворота должен быть равен нулю.
Если это условие с заданной точностью выполнено, то расчет прекращается, и выдаются
на печать результаты; если условие не выполнено, то производится корректировка
граничного условия на левом краю: если   0, то изменяется нижняя граница начального
угла поворота 01   , и, наоборот, если   0, то 02   ; вычисляется новое значение
начального угла поворота 0  01  02  / 2 .
На рис. 3 показаны также результаты расчета – эпюры прогибов в масштабе балки
для различных значений силы, а на рис. 4 приведена диаграмма «сила – прогиб», на
которой точками показаны результаты наших первых экспериментов.
3. Продольно-поперечный изгиб возникает в случае, когда балка лежит на двух
цилиндрических неподвижных опорах, позволяющих изгибаемой балке соскальзывать по
направлению касательной к оси балки в точках опирания (рис. 5). Расчет ведется
аналогично п. 2 со следующими отличиями: первой прирастающей величиной является не
s, а z, и изгибающий момент вычисляется по формуле m  z   2 f  z  wtg0  / l .
f
3 l  210 мм h  8 мм
2
1
wmax , cм
1
2
3
4
5
Рис. 4
Рис. 5
На рис. 5 изображены изогнутые оси в упругом и пластическом состоянии, которое
наступает резко, так в рассматриваемом случае скачок происходит от w  10,36 мм при
f  1, 26 до w  64,9 мм при f  1, 26213 .