Подбор необходимой площади сечения напрягаемой

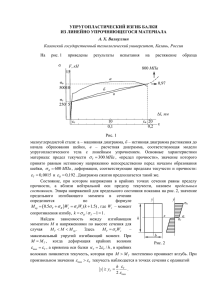
Этап 5. Расчет и конструирование предварительно напряженной
подкрановой балки
Подкрановые балки работают на подвижную динамическую нагрузку
от мостовых кранов, воспринимая большие сосредоточенные силы
давления крановых колёс и испытывая одновременное воздействие
вертикальных и горизонтальных (от торможения крановой тележки)
нагрузок.
В практике проектирования существует два основных варианта
компоновки железобетонных подкрановых конструкций: двутавровая
подкрановая балка и тавровая со сжатыми полками.
К подкрановым конструкциям относятся:
- подкрановые балки;
- вертикальные и горизонтальные связи, обеспечивающие необходимую
жёсткость и неизменяемость конструкции;
- крановые рельсы с креплениями и упорами.
Расчет железобетонных конструкций на выносливость производится
при воздействии многократно повторяющейся (подвижной или
пульсирующей) нагрузки, вызывающей значительный перепад напряжений
в бетоне или растянутой арматуре, если число повторений нагрузки за
период эксплуатации здания или сооружения достаточно велико (порядка
105 и более). Основным параметром, характеризующую динамическую
нагрузку является коэффициент асимметрии цикла ρs.
В зависимости от значения ρs по таблицам Приложений 4 и 6
определяются коэффициенты условий работы бетона γb и арматуры
растянутой зоны γs4 и γs5.
Для снижения учебной нагрузки в курсовом проектировании
установлены предположения:
1. трещины в растянутой зоне не образуются;
2. горизонтальные усилия полностью воспринимаются тормозной
конструкцией и не передаются на подкрановую балку;
3. напряжения в арматуре с учетом всех потерь - 0,7σsp.
Допущения позволяют рассматривать сечение подкрановой балки как
упругое тело и не рассматривать сжатую полку при действии
горизонтальных крановых нагрузок.
Основные конструктивные требования
Класс бетона балок принимается не ниже В30.
Минимальный процент армирования принимается – 0,2%.
Расстояние в свету между продольными стержнями должно быть не
более 300 мм.
Максимальный шаг хомутов на опоре 300мм.
Минимальный диаметр боковых стержней при h ≤ 1500 составляет
10мм, при большей высоте 14 мм.
5.1. Нагрузки, действующие на подкрановую балку
Расчёт подкрановой балки обычно производят на совместное
действие двух сближенных кранов с грузовыми тележками, тормозящими
вблизи балки. Расчётные значения вертикальных и горизонтальных
крановых нагрузок определяют по формулам:
P = Pmax,nγ f γ n kd 1ψ , T = Tnγ f γ n kd 2ψ .
(5.1)
где: Рmax,n - нормативная сила вертикального давления колеса крана на
рельс принимается по ГОСТ 6711-81, ГОСТ 25711-83 или приложению 17;
γf - коэффициент надёжности по нагрузке для крановых нагрузок,
принимаемый по указаниям пункта 4.8. [4]; γn- коэффициент надёжности
по ответственности, принимаемый по указаниям приложения 7* [4]; kd1,
kd2-коэффициенты динамичности, принимаемые по указаниям пункта 4.9.
[4]; ψ - коэффициент сочетаний, принимаемый по указаниям пункта 4.17.
[4]; Тn - нормативная горизонтальная нагрузка, приходящаяся на одно
колесо крана; То - полная нормативная горизонтальная нагрузка,
вызываемая торможением тележки крана и определяемая по указаниям
пункта 4.4. [4]; n0 - число колёс с одной стороны крана. При расчёте балок
под краны с группами режимов работы 7К и 8К вместо горизонтальной
нагрузки, вызываемой торможением тележки крана, учитывают
воздействие горизонтальных сил бокового давления, вызываемого
перекосом моста крана и непараллельностью крановых путей. Расчётное
значение данной горизонтальной нагрузки на одно колесо крана:
(5.2)
T = 0,1P γ γ k ψ
t
n
f
n d2
5.2. Определение максимально возможных внутренних усилий в
подкрановой балке для расчетов по I группе предельных состояний
Максимально возможный изгибающий момент в разрезной балке,
нагруженной системой взаимосвязанных подвижных грузов, возникает в
том случае, если равнодействующая этой системы грузов и ближайший к
ней груз равноудалены от середины пролёта балки. Максимальный
изгибающий момент возникает в этом случае в сечении, расположенном
под этим грузом (правило Винклера).
Пример реализации этого правила представлен на рис. 5.1, когда на
рассматриваемую балку умещается три колеса (три подвижных груза) двух
сближенных кранов (габариты кранов см. приложение 17).
Для определения максимально возможной перерезывающей силы в
балке от вертикальной нагрузки краны располагают таким образом, чтобы
одно из колёс (один из грузов) находилось на расстоянии не мене h0 от
опоры, а остальные - как можно ближе к ней (рис. 5.2).
5.3. Определение количества продольной и поперечной
арматуры
Подбор необходимой площади сечения напрягаемой арматуры
рассматривается в блок-схеме 5.1.
Подбор площади сечения продольной напрягаемой арматуры
растянутой зоны
блок-схема 5.1 (начало)
1. Начало
. Геометрические характеристики сечения балки
Характеристики бетона и арматуры (см. прил. 2, 3)
3. h0 = h − as
Рис. 5.1. К определению максимального изгибающего момента в
подкрановой балке.
Расчётные внутренние усилия в балке от действия вертикальных
крановых нагрузок определяются с учётом собственного веса подкрановых
конструкций:
Mmax =Mmax,p +Mw;
(5.3)
Qmax =Qmax,p + Qw.
где: Qw – поперечное усилие от собственного веса балки;
Mw – изгибающий момент в сечении от собственного веса балки.
нет
да
4. M
max
≤ Rb b h ( h0 − 0, 5 h )
'
f
'
f
'
f
'
'
'
4б. α = M max − Rb (b f − b)h f (h0 − 0,5h f )
m
2
Rbbh0
4а. α = M max
m
Rb b 'f h02
5. ξR по приложению 5 табл. 2
при σsp/Rs = 0,6
6.
Рис. 5.2. Возможное неблагоприятное расположение кранов для
наклонного сечения подкрановой балки
αR = ξR(1- 0,5·ξR)
блок-схема 5.1 (окончание)
Нет
7. α
m
≤ αR
Подбор поперечной арматуры
Блок-схема 5.2 (начало)
1. Начало
Да
2. Геометрические характеристики сечения балки
Характеристики бетона и арматуры (см. прил. 2,3)
7б.
A's =
Мmax −αR Rbbh02 − Rb (b'f − b)h'f (h0 − 0,5h'f )
Rsc (h0 − a 's )
3. A1= b·h
4. P = 0,7 Aspγ spσ sp
8. ξ=1− 1−2αm
5. ϕ = 1 + 1, 6 ⋅ P( 2 ) − 1,16  P( 2) 


n
Rb A1
 Rb A1 
9. γ = 1, 25 − 0, 25 ξ ≤ 1,1
s3
ξR
Нет
10. A = ξRbbh0
sp
γ s3 Rs
6 . ai = ci /ho < 3
6б. а0i = 3
Да
6а. а0i = аi ≤ 2
Конец
7.
Нет
8б. q = 0, 25ϕ R b
sw ( i )
n bt
2
ε гр i =
8. ε =
i
1,5
ai
0, 75a0i
εi −
1,5
+ 0,1875a0i
ai
Qi
≤ ε гр i
ϕ n Rbt bh0
Да
8a. q = 0, 25ϕ R b ε грi
sw ( i )
n bt
εi
блок-схема 5.2 (продолжение)
Нет
9.
блок-схема 5.2 (окончание)
Да
i=2
Нет
Да
17. Qmax i ≤ Qbi + Qswi
9б. Переход в п.6
Нет
Да
10. q sw 1 < q sw 2
10б. qsw = qsw1
17а. Прочность
сечения обеспечена
17б. прочность сечения не
обеспечена. Увеличить
класс бетона, Rsw, qsw
10а. q sw = q sw2
11. i = 1
Нет
18.
i=2
Да
18б. Переход в п.13
Конец
12. Asw, sw по конструктивным
требованиям п.5.2 [2]
5.4. Расчет подкрановой балки на выносливость
13. q =
swi
Нет
Rsw Aswi
swi
14. 2h0 + li < ci
14б. c0 = сi ≤ 2 h0
Да
14а. Qsw = 1,5qsw (i +1) h0
15.Qsw = 0,75[qswiсо- (qswi -qsw(i+1) )(ci-li)]
Нет
16б. Qbi =0,5φnRbtbho
16. ci ≤ 3h0
Подкрановые балки при среднем и тяжелом режимах работ мостовых
кранов необходимо рассчитывать на выносливость, при этом если в
расчете на прочность учитывается одновременная работа двух кранов в
одном пролете, то согласно указаниям п. 1.7 [4] проверку на выносливость
следует производить на нормативную нагрузку только от одного крана с
давлением колес:
Pd = k ⋅ γ n ⋅ Pn ,
(5.4)
где: k =0,5 – коэффициент понижения нормативного значения нагрузки,
принимаемый по указаниям п. 1.7 [4].
5.5.1 Расчет на выносливость сечений, нормальных к продольной оси
Расчет выносливости элементов, должен производиться из условий:
а) для сжатого бетона
σb,max ≤ Rb,
Да
16а. Q = 1, 5ϕn Rbt bh02
bi
ci
(5.5)
где σb,max - максимальное нормальное напряжение в сжатом бетоне;
Rb – расчетное сопротивление бетона сжатию умноженное на коэффициент
условий работы γb1.
б) для растянутой арматуры
σs,max ≤ γs4γs5 Rs
(5.6)
где
σs,max – максимальное напряжение в растянутой арматуре,
определяемое по формуле
(5.7)
σs,max = α·σbs + σsp,
здесь α =Es/Eb– коэффициент приведения арматуры к бетону;
σbs – напряжение в бетоне на уровне наиболее растянутого ряда арматуры;
σsp – принимается с учетом всех потерь и коэффициента γsp = 0,9;
Rs – расчетное сопротивление растянутой арматуры, умноженное на
коэффициент условий работы γs4 (таблица 1 приложение 6), а при наличии
сварных соединений - также на коэффициент γs5 (таблица 2 приложение 6).
В зоне, проверяемой по сжатому бетону, при действии многократно
повторяющейся нагрузки следует избегать возникНовения растягивающих
напряжений, иначе в сжатую зону устанавливается предварительно
напрягаемая арматура. При этом сжатая арматура на выносливость не
рассчитывается.
При расчете на выносливость приведенное сечение принимается
следующим образом: если в сечении не образуются нормальные трещины,
т.е. если выполняется условие:
M crc = γ Rbt , serWred + P(e0 p + r )
(5.8)
при замене в нем значения Rbt,ser на Rbt (при учете γb таблица 4 приложение
2), приведенное сечение включает в себя полное сечение бетона, а также
площадь сечения всей продольной арматуры, умноженной на коэффициент
приведения α. Обозначения в формуле (5.8) см. Методические указания
«Расчет изгибаемых железобетонных элементов c предварительным
напряжением арматуры по II-ой группе предельных состояний».
В курсовом проекте значение усилия обжатия Р(2) с учетом всех
потерь, допускается определять по формуле 0,7γspσspAsp.
Если условие (5.8) не соблюдается, то есть трещины образуется,
приведенное сечение определяется без учета работы растянутой зоны.
5.4.2 Расчет на выносливость сечений, наклонных к продольной оси
Расчет на выносливость сечений, наклонных к продольной оси
элемента, должен производиться из условия, что равнодействующая
главных растягивающих напряжений, действующих на уровне центра
тяжести приведенного сечения, должна быть полностью воспринята
поперечной арматурой при напряжениях в ней, равных сопротивлениям Rs,
т.е. должно выполняться условие:
σ
mt
≤

σ +σ y
Rs Asw Rs As ,inc
+
sin θ  sin θ + cos mt

bs
bsinc
τ xy


 ,

(5.9)
где σmt - главное растягивающее напряжение на уровне центра тяжести
приведенного сечения, вычисляемое по формуле 5.11;
σy, τху - соответственно сжимающее напряжение в направлении,
перпендикулярном продольной оси, и касательное напряжение,
определяемые на том же уровне, что и напряжение σmt;
Rs - расчетное сопротивление хомутов и отгибов с учетом коэффициентов
условий работы γs4 и γs5 (см. приложение 6);
θ - угол наклона отгибов к продольной оси элемента на уровне центра
тяжести сечения в рассматриваемом сечении;
sinc - расстояние между плоскостями отгибов, измеренное по нормали к
ним; при одной плоскости отгибов за sinc принимается расстояние между
этой плоскостью и гранью опоры; при двух и более плоскостях отгибов
значение sinc определяется согласно рис. 5.3.
Рис. 5.3. Учет отогнутых стержней при расчете наклонных сечений на
выносливость 1-1, 2-2 - плоскости отгибов; для 1-1 sinc = (sinc1 + sinc2)/2; для
2-2 sinc = sinc2; l1 и l2 - длины участков элемента при учете соответственно
плоскостей отгибов 1-1 и 2-2
Для элементов, в которых поперечная арматура не предусматривается,
должны быть выполнены требования
σ
mc
σ
mt
≤ Rb ,
≤ Rbt .
(5.10)
где: Rb и Rbt, расчетное сопротивление бетона при сжатии и растяжении
соответственно, умноженные на коэффициент условий работы γb согласно
таблице 2 Приложения 4.
Значения главных растягивающих и главных сжимающих напряжений
в бетоне σmt и σmc определяется по формуле:
σ mt = m
mc
σx +σ y
2
2
 σ −σ y 
2
+  x
 + τ xy .
2


Q S red
,
b I red
(5.12)
где: Q - поперечная сила от внешней нагрузки в рассматриваемом сечении;
при этом следует учитывать возможность отсутствия временной нагрузки
на участке от опоры до рассматриваемого сечения;
Sred - приведенный статический момент части сечения, расположенной
выше рассматриваемого волокна, относительно оси, проходящей через
центр тяжести приведенного сечения;
b - ширина сечения балки на уровне рассматриваемого волокна.
Коэффициенты условий работы бетона γb, применяемые при действии
многократно повторяющейся нагрузки, определяются в зависимости от
коэффициента асимметрии цикла ρb:
ρb =
σ b , min
σ b ,max
,
γb = 0,7 - 0,06ρb.
(5.11)
где σх - нормальное напряжение в бетоне на площадке, перпендикулярной
продольной оси элемента, от внешней нагрузки и усилия предварительного
обжатия Р, при этом σх принимается равным напряжению в бетоне σb;
σу - нормальное напряжение в бетоне на площадке, параллельной
продольной оси элемента, от местного действия опорных реакций,
сосредоточенных сил и распределенной нагрузки (см. п. 4.10 [3]), а также
от усилия обжатия вследствие предварительного напряжения хомутов и
отогнутых стержней (см. п. 4.11 [3]);
τху - касательное напряжение в бетоне от внешней нагрузки и усилия
обжатия вследствие предварительного напряжения отогнутых стержней.
Касательные напряжения в бетоне τxy следует определять по формуле:
τ xy =
принимаются сжимающие напряжения. В этом случае коэффициент γb для
тяжелого бетона естественной влажности при 0 > ρb ≥ -5 определяется по
формуле:
(5.13)
где σb,min, σb,max - соответственно наименьшее и наибольшее напряжение в
бетоне в пределах цикла изменения нагрузки, при этом напряжения
принимаются со своими знаками: при проверке условия (5.10) за
положительные принимаются напряжения сжатия, а при проверке условий
(5.5) - напряжения растяжения.
При ρb ≥ 0 коэффициент γb принимается по таблице. 5.2.
При определении расчетного сопротивления Rb или Rbt,, если
напряжение растяжения сменяется напряжением сжатия, за величину σb,min
(5.14)
При γb = 1,00 расчет на выносливость сжатого бетона можно не
производить.
При проверке образования наклонных трещин коэффициенты условий
работы γb, вводимые на расчетные сопротивления Rbt и Rb, определяются
соответственно по зависимостям:
ρb =
σ mt ,min
σ mt ,max
и ρb =
σ mc ,min
σ mc ,max
,
(5.15)
где:
σmc,min, σmc,max, σmt,min, σmt,max - соответственно наименьшие и
наибольшие главные сжимающие и главные растягивающие напряжения в
бетоне в пределах цикла изменения нагрузки, определяемые по формуле
5.11 по полному приведенному сечению.
Коэффициент условия работы арматуры γs4, принимают при расчете
на выносливость и определяют по таблице 1 Приложения 6. При наличии
сварных соединений учитывается дополнительный коэффициент условий
работы γs5, определяемый по таблице 2 Приложения 6.
При расчете на выносливость продольной растянутой арматуры
коэффициент асимметрии цикла ρs определяется по формуле:
ρs =
s , m in
,
σ s , m ax
(5.16)
где σs,min, σs,max - соответственно наименьшее и наибольшее напряжения в
растянутой арматуре в пределах цикла изменения нагрузки, определяемые
согласно п. 5.1; при этом растягивающие напряжения принимаются со
знаком «плюс», а сжимающие напряжения - со знаком «минус».
При расчете на выносливость поперечной арматуры значение ρs
определяется по формуле:
ρs =
σ mt , min
σ mt , max
,
(5.17)
где σmt,min, σmt,max - соответственно наименьшие и наибольшие главные
растягивающие напряжения в бетоне в пределах цикла изменения
нагрузки, определяемые по формуле 5.11.
При вычислении напряжений и усилий, входящих во все формулы для
ρs, используются те же нагрузки, что и при расчете на выносливость.
Проверка выносливости сжатого бетона
блок-схема 5.3 (продолжение)
блок-схема 5.3 (начало)
Начало
9.
+
1. Mmax, Mmin, Mw, Eb, Es, b, h, b'f, h'f, bf, hf, As
A's, Asp, A'sp, as, a's, asp, a'sp, P(2), e0 p
2.
Ib =
(b
f
(
)
− b hf
12
3
hf 


+ b f − b h f  y t −
2 

(
)
I sp = Asp ( yt − asp ) ,
2
σ sp = 0,8 Rsn − Вр1200, Вр1400, К1200, К 1400
4. α = Es Eb
10. eop =
11. σ
6. Ared = Ab + α (As + As′ + Asp + Asp
′ )
h′

h
f
= bh +  b′ − b  h '  h −
red
2  f
2
 f 

2
(
′ h − yt − a'sp
I 'sp = Asp
)2
Aspσ sp ysp − Asp′ σ sp′ ysp′
5. Ab = bh + (b′f − b )h′f + (b f − b )h f
S
2
)
9b. I red = I b + αI s + αI ' s +αI sp + αI ' sp
3. P = Aspγ sp ( 0, 7 ⋅ σ sp )
7.
(
I s = As ( yt − as )2 , I 's = As′ (h − yt − a's )2 ,
9a.
σ sp = 0,9 Rsn − А540... А1000
)
3
2
b ′f − b h ′f
h ′f


bh 3
h

− y t  +
+ bh y t −  +
+ b ′f − b h ′f  h −
12
2
12
2



h

f
 +  b − b  h
+ α A a + α A′ h − a ′ +
s s
s
s
  f
 f 2

(
)
нет
+α A a + α A '  h − a ′ 
sp sp
sp 
sp 
b ,max
=
P(2)
Ared
−
P(2)
P(2) e0 p (h − yt )
I red
+
M max (h − yt )
I red
12. σ
b ,max ≤ Rb
да
S red
8. yt =
Ared
Прочность
сжатого бетона
не обеспечена
P(2) P(2) e0 p (h − yt ) M min (h − yt )
13. σ
−
+
b ,min =
Ared
I red
I red
14. ρb = σb,min/σb,max
блок-схема 5.3 (окончание)
блок-схема 5.4 (окончание)
нет
15. γb - по табл. 2 приложения 4
нет
6а. Повысить
Rs, As, класс бетона
17. σb,max ≤ γb Rb,
конец
конец
Проверка выносливости растянутой арматуры
блок-схема 5.4 (начало)
Начало
1. Mmax, Mmin, Eb, Es, Rs, Ired, Ared, σsp, yt,
asp, P(2).
σ s ,max
6б. Прочность
обеспечена
17б. Прочность
обеспечена
17а. Повысить класс
бетона, As′
2.
да
6. σs,max ≤ γs4 γs5Rs
Проверка выносливости наклонных сечений
Расчет на выносливость наклонных сечений производят из условия,
что
равнодействующая
главных
растягивающих
напряжений,
действующих на уровне центра тяжести приведенного сечения, должна
быть полностью воспринята поперечной арматурой при напряжениях в
ней, равных расчетным сопротивлениям Rs .
Для элементов, в которых поперечную арматуру не предусматривают,
должны быть выполнены условия 5.10 с введением в эти условия вместо
расчетных сопротивлений бетона Rbt ser и Rb ser соответственно расчетных
сопротивлений Rbt и Rb, умноженных на коэффициент условий работы γb по
таблице 5.2 (см. п. 5.4).
блок-схема 5.5 (начало)
Начало
 M ( y − asp ) P(2) P(2) e0 p ( yt − asp ) 
= α  max t
−
−
 + σ sp
I red
Ared
I red


1. Mmax, Qmax, Qmin, Eb, Es, Rs, Ired,
Ared, σsp, asp, P.
3.
σ s ,min
Pe ( y − a p ) 
 M ( y − ap ) P
= α  min t
−
− 0p t
 + σ sp
I red
Ared
I red


4. ρ = σ s ,min
s
σ s ,max
5. γs4, γs5 по приложению 6
2.
S′
=b
red
( h − yt ) 2
2
(
)
h'f 

+ b ' f − b h '  h − yt −
+
f 
2 
(
+ α A ′ ( h − y t − a ' s ) + α A′
h − yt − a ′sp
s
sp
)
блок-схема 5.5 (продолжение)
′
Qmax S red
3. τ
xy , max =
I red b
′
Qmin S red
4. τ
xy , min =
I red b
5. σ x , max = σ x , min =
P(2)
Ared
2
σ x ,max
σ

6. σ
+  x ,max  + τ xy2 ,max
mt ,max = −
2
 2 
Пример расчета.
В курсовом проекте на 5 этапе необходимо спроектировать
железобетонную подкрановую балку с подбором продольной и поперечной
арматуры и проверить выносливость сечений нормальных и наклонных к
продольной оси балки.
По результатам компоновки поперечной рамы определены основные
геометрические характеристики подкрановой балки (см. этап 1).
Размеры поперечного сечения: b'f = 650 мм, h'f = 160 мм, b = 140 мм, hf
=250 мм, bf = 340 мм, h = 1200 мм (см. рис. 5.4). Пролет L=12м. Толщина
защитного слоя бетона назначаем с учетом требований п.5.7. [3], величину
аs принимаем равной 40 мм.
Механические характеристики бетона и арматуры: бетон для
предварительно напрягаемых конструкций по заданию В30 определяем по
Приложению 2 и 3 методических указаний (Rb= 17 МПа, Rbt = 1,15 МПа),
γb1=1; класс напрягаемой арматуры К1400 (Rs= 1170 МПа). Ненапрягаемая
конструктивная арматура А400.
2
σ x ,min


7. σ
+  x ,min  + τ xy2 ,min
mt , min = −
2
 2 
8 ρs =
9. γs4, γs5
10. σ
Нет
11а. Повысить
Rs, Asw, s
σ mt , min
σ mt , max
.
по приложению 6
mt ult
=
γ s 4,γ s 5 Rs Asw
11. σmt ≤
bsw
σ mt ult
Рис. 5.4. Поперечное сечение подкрановой балки
Да
11б. Прочность
обеспечена
конец
5.2 Определение усилий в подкрановой балке
По Приложению 17 определяем габариты крана грузоподъемностью
32/5 и пролетом 18 м: база Ак=5,1м, ширина Вк=6,3м.
По формуле 5.1 методических указаний находим максимальное
давление колеса крана:
P =235·1,1·0,95·1·0,85=208,74кН.
Выполняем правило Винклера (см п. 5.1). Для данного
рассматриваемого случая (рис. 5.5), учитывая, что количество колес в
пролете балки n=3, расстояние от равнодействующей системы сил 3Р и до
ближайшего колеса крана х можно определить по формуле:
Р( АK − ( Bк − АK ))
;
3Р
208,74 ⋅ ( 5,1 − ( 6 ,3 − 5,1 ))
х=
= 1,3 м .
3 ⋅ 208,74
x=
Далее по линии влияния или из условий равновесия сил,
последовательно, строим эпюру изгибающих моментов. Наибольший
изгибающий момент от вертикальных крановых нагрузок в сечении балки
под колесом, ближайшим к середине пролета балки. Из уравнения
равновесия получаем: Мmax,p=1224кНм, тогда расчетный момент, с учетом
собственного веса, равен:
 l 2 х2 
М max = М max, p + q  0 −  ;
8 
 8
 11,8 2 1,3 2 
−
М max = 1224 + 9,13 
 = 1384,6 кНм ,
8 
 8
где:
q = m·γf·γn /l0 - расчетный погонный собственный вес подкрановой балки;
l0 = L–0,5bk =12–0,2=11,8м - расчетный пролет балки, m – масса балки;
bk – ширина поперечного сечения колонны.
q = 103·1,1·0,95/11,8 = 9,13 kH/м.
Рис. 5.5. Определение максимального изгибающего момента
5.3. Определение площади сечения арматуры
Расчет выполняем по блок-схеме 5.1.
1. Начало.
2. Характеристики бетона и арматуры см. выше.
3. Рабочая высота сечения: h0 =1200 – 40 = 1160 мм. Расчет ведем согласно
п.3.19[2] в предположении, что сжатой ненапрягаемой арматуры не
требуется.
4. Проверяем условие (3.23) [2]:
17·(1000)⋅0,65⋅0,16 (1,16− 0,5⋅0,16) = 1954 кНм > Mmax = 1384,6кНм, т.е.
граница сжатой зоны проходит в полке, и расчет производим как для
прямоугольного сечения шириной b = b'f =650 мм согласно п.3.14 [2].
4. Определим значение относительно момента αm :
1384, 6
αm =
= 0, 09.
17 ⋅ (1000) ⋅ 0, 650 ⋅1,162
По табл. 2 Приложения 5 при классе арматуры К1400 и σsp/Rs = 0,6 находим
ξR = 0,34.
6. 7. Тогда αR =0,34(1-0,34/2) = 0,28 > αт = 0,09, т.е. сжатой арматуры
действительно не требуется, и площадь сечения растянутой арматуры
вычисляем по формуле (3.10) [3].
8. Определяем коэффициент ξ:
ξ = 1 − 1 − 2 ⋅ 0, 09 = 0, 094,
и коэффициент γs3 согласно п.3.9. [2].
9. Так как ξ/ξR = 0,094/0,31 < 0,6 принимаем γs3=1,1.
10. Тогда при As = 0, площадь напрягаемой арматуры равна:
Asp =
0, 094 ⋅17 ⋅ 650 ⋅1160
= 936, 2 мм 2 .
1,1⋅1170
Принимаем 6∅15 К1400 (Аsр = 1059,75 мм2). Расположение
арматуры в два ряда с учетом конструктивных требований п. 5 [2] как
показано на рис. 5.6.
Из-за двух рядового расположения продольной ПН арматуры рабочая
высота балки будет равна h0 = 1140мм.
Рис. 5.7. К расчету по наклонным сечениям (размерности кН и мм).
тогда
2
747,8
747,8


− 1,16 ⋅ 
 = 1, 34.
3
3
17 ⋅10 ⋅ 0,168
 17 ⋅10 ⋅ 0,168 
6. Определим требуемую интенсивность хомутов согласно п. 3.34,а [6], у
первого колеса i=1, принимая длину проекции наклонного сечения с,
равной расстоянию от опоры до первого груза – с = с1 = 2,28 м.
Так как a1 =2,28/1,14 = 2 < 3, и следовательно, а01 = а1 = 2.
7. Определим коэффициент:
1,5
ε гр1 =
+ 0,1875 ⋅ 2 = 1,125.
2
8. Поперечная сила на расстоянии с1 от опоры, с учетом собственного веса
балки, равна (см. рис. 5.7):
q (l − 2c1 )
;
Q1 = Qmax,1 + 0
2
Q1 = 372, 6 + 33, 05 = 405, 65 кН .
Поскольку
Q1
405, 65
ε1 =
=
= 1,645 > ε гр1 = 1,125,
ϕ n Rbt bh0 1, 34 ⋅1,15 ⋅ (1000) ⋅ 0,14 ⋅1,14
значение qsw(1) определяем по формуле (3.58) [6]:
ϕ n = 1 + 1, 6 ⋅
Рис. 5.6. К подбору продольной предварительно напрягаемой арматуры
Продолжаем расчет по сечениям, наклонным к продольной оси балки
по блок-схеме 5.2.
Требуется определить диаметр и шаг поперечных стержней
(хомутов), а также выяснить их шаг в двух точках колес i=1;2. При расчете
по наклонным сечениям балки таврового или двутаврового сечения свесы
полок не учитывается (в запас), поэтому рассматривается прямоугольное
сечение b×h =140×1200 мм.
Начало.
1. По указаниям п. 5.2. методических указаний определяем усилия,
действующие в опорной зоне подкрановой балки (рис. 5.7).
2. Согласно рис. 5.4, имеем: b = 140 мм, h = 1200 мм , h0 = 1140мм. Другие
данные указаны выше.
3-5. По формуле (3.53а [2]) определим коэффициент φn, принимая A1= b·h =
=0,140·1,2=0,168м2 и приближенно усилие обжатия Р(2) при канатной
арматуре К1400 равно:
P(2) = 0, 7 ⋅ (1059, 75 ⋅10 −6 ) ⋅ 0,9 ⋅ (0,8 ⋅1400 ⋅103 )=747,8 кН .
qsw (1)
1,5
2 = 129, 07 kH .
= 0, 25 ⋅1, 34 ⋅1,15 ⋅103 ⋅ 0,14 ⋅
0, 75 ⋅ 2
м
1, 645 −
9. Так i < 2 повторно определим значение qsw(2) при значении сi, равном
расстоянию от опоры до второго груза – с2 = 3,48 м.
c=
a2 = с2/hо = 3,48/1,14 = 3,05 > 3, следовательно, а2 = 3. Тогда а02 = 2.
1, 5
+ 0,1875 ⋅ 2 = 0,875.
3
Соответствующая поперечная сила на расстоянии от опоры с2 с учетом
собственного балки веса равна:
 l − 2с2 
Q2 = Qmax,2 + q  0
;
 2 
ε гр 2 =
Q2 = 163,8 + 22,1 = 185,9 кН .
Поскольку
ε2 =
185, 9
= 0, 754 < 0,875,
1, 34 ⋅ 1,15 ⋅ 1000 ⋅ 0,14 ⋅1,14
тогда
kH
0,875
= 62,8
.
0, 754
м
10. Принимаем максимальное значение qsw = qsw(1) = 129,07кН/м.
11. Согласно п. 5.12 [6] шаг sw1 у опоры должен быть не более 0,5ho =
=580мм и не более 300мм, а в пролете - не более 3/4ho = 870мм и не более
600мм. Принимаем шаг кратно 50, т.е. sw1 = 300мм, а в пролете sw2 = 600мм.
12. Требуемая площадь поперечной арматуры:
129, 07 ⋅ 0, 3
q ⋅s
Asw1 = sw w1 =
⋅ 10 6 = 135,87 мм 2 .
Rsw
285 ⋅ 103
Принимаем хомуты диаметром 10 мм в 2 ряда (Аsw = 157мм2).
13. Тогда значение интенсивности установки поперечных стержней у
опоры равно:
qsw (2) = 0, 25 ⋅1, 34 ⋅1,15 ⋅103 ⋅ 0,14 ⋅
qsw1 =
Asw1 Rsw 157 ⋅10 −6 ⋅ 285 ⋅103
kH
=
≈ 149, 2
.
sw
0, 3
м
14,15. Длину участка с шагом хомутов sw1 определяем из условия
обеспечения прочности согласно п. 3.35 [6]. При этом qsw2=0,5qsw1=74,6
кН/м. Зададим длину участка с шагом хомутов sw1, равной расстоянию от
опоры до первого груза l1 = 2,28м и проверим условие прочности п. 3.50
[6]. Так как 2ho + l1 = 2·1,14 + 2,28 = 4,56м > с1 = 2,28м, значение Qsw
определяем по формуле 3.64 [6], принимая с1=сo = 2,28м < 2ho = 2,32м:
Qsw2 = 0,75·[149,2·2,28 – 74,6·(0)] =255,18кН;
16. Значение проекции наклонной трещин:
с1 = 2,28 м < 3ho = 3·1,14 = 3,42м.
c=
1, 5ϕ n R bt bh02
0, 75q sw1
1, 5 ⋅1, 34 ⋅1150 ⋅ 0,14 ⋅1,14 2
= 1, 94 м.
0, 75 ⋅149, 2
Принимаем c=с1=2,28м.
1, 5 ⋅1,34 ⋅1150 ⋅ 0,14 ⋅1,16 2
= 184, 93кН .
Qb1 =
2, 28
17. Так как Qb1 + Qsw1 = 184,93+255,18 = 440,1кН < Q1 = 405,65кН, т.е.
прочность наклонного сечения с интенсивностью хомутов qsw1 обеспечена.
Выполним проверку прочности при значении сi, равном расстоянию
от опоры до второго груза, но не более 0,5·l0. Так как l2 =3,48 > 0,5·11,8
=5,9м, принимаем с2 = 3,48м.
Поскольку c2 > 2ho , принимаем сo = 2ho = 2,28м. Тогда при 2ho + l1 =
2·1,14 + 2,28 = 4,56м > с1 = 3,48м, значение Qsw определяем по формуле
3.64 [6],
Qsw2 = 0,75·[149,2·2,28 – 74,6·(3,48-2,28)] =188кН;
При с2 = 3,48м > 3ho = 3·1,14 = 3,42м значение Qb соответствует его
минимальному значению:
Qb2 = Qb,тiп = 0,5φn·Rbt·b·h0;
Qb2 = 0,5·1,34·1,15·103·0,14·1,14 = 123,3кН.
Проверка несущей способности:
Qb2 + Qsw2 = 123,3 + 188 = 311,3кН > Q3 = 185,9кН,
т.е. прочность наклонного сечения, расположенного под вторым грузом
обеспечена.
Таким образом, в подкрановой балке в опорных участках на длину l =
2,4м устанавливаем хомуты с шагом sw1= 300мм, а в пролетной части с
шагом sw2 = 600мм.
5.4 Расчет выносливости сечений, нормальных и наклонных к
продольной оси подкрановой балки
5.4.1. Расчет на выносливость сжатого бетона (блок-схема 5.3).
1. Начало.
Расчет на выносливость подкрановой балки ведем на основании [3]. При
расчете на выносливость рассматривается нагрузка только от одного крана
(рис.5.9). Давление от одного колеса при расчете на выносливость
определяется по формуле 5.5:
Pd = 0,5·0,95·235=111,63 кН.
6. Статический момент приведенного сечения относительно растянутой
грани сечения балки:
0,16 
0, 25

S
= 0,14 ⋅1, 2 ⋅ 0, 6 + ( 0, 65 − 0,14 ) ⋅ 0,16 ⋅  1, 2 −
+
 + ( 0,34 − 0,14 ) ⋅ 0, 25 ⋅
red
2 
2

+5,538 ⋅ 0, 001060 ⋅ 0, 06 + 6,154 ⋅ 0,000226 ⋅ (1, 2 − 0, 04 ) = 0,194м 3 .
7. Расстояние от оси арматуры до центра приведенного сечения:
0,194
yt =
≈ 0, 64 м .
0,307
8-9b. Момент инерции приведенного сечения Ired = 0,055м4.
10. Определяем эксцентриситет усилия обжатия:
eop = ysp = yt − as = 0, 64 − 0, 04 =0,6м.
Рис. 5.9. К расчету нормальных сечений на выносливость.
Максимальный нормативный изгибающий момент с учетом собственного
веса:
l 2 A 2 
M max = M max,d + q  0 − k  ;
 8 32 
 11,8 2 5,12 
M max = 395 + 8,29 
−
 ≈ 527,7 kHм.
32 
 8
Нормативный изгибающий момент от собственного веса балки Mw, n:
l 2 A 2 
M min = M w, n = qn  0 − k  ;
 8 32 
 11,82 5,12 
M min = 8, 29 
−
 ≈ 137,5 kHм.
32 
 8
где qn = m· γn /l0 =103·0,95/11,8 = 8,29 kH/м.
2. Величина обжатия сечения предварительно напряженной арматурой:
P(2) = 747,8кН ;
3. Так как предполагаем, что трещин в растянутой зоне нет - коэффициент
приведения для канатной арматуры К1400 равен:
α = 180000 / 32500 = 5, 538,
для стрежневой конструктивной арматуры А400:
α s = 200000 / 32500 = 6,153.
4,5. Площадь приведенного сечения балки с учетом конструктивных
стержней:
Ared = 0,307м2.
11. Максимальные сжимающие напряжения в бетоне:
747,8 747,8 ⋅ 0, 6 ⋅ (1, 2 − 0, 64) 527,7(1, 2 − 0, 64)
σ b ,max =
−
+
=
0,307
0,0573
0,0573
= 3153 kH/м 2 = 3,15МПа < Rb = 17 МПа.
12. Прочность сжатого бетона при однократном воздействии крановом
воздействии обеспечена.
13. Минимальные напряжения в бетоне сжатой зоны:
747,8 747,8 ⋅ 0, 6 ⋅ (1, 2 − 0, 64) 137,5(1, 2 − 0, 64)
−
+
=
σ b ,min =
0,307
0,0573
0,0573
= −655 kH/м 2 = −0, 655 МПа < Rbt = 1,15МПа.
знак «минус», значит, верхняя полка подкрановой балки до приложения
вертикальной крановой нагрузки растянута, но трещины не образуются.
14. Определяем коэффициент асимметрии цикла:
ρb = -0,655/3,15 = -0,208.
15, 16. Согласно п. 5.3. при отрицательном значении коэффициента
асимметрии коэффициент определяем по формуле 5.14:
γb = 0,7-0,06·0,208=0,68.
17. Так как σb,max ≤ γbRb=0,68·17=11,5 МПа, выносливость сжатого бетона
обеспечена.
5.4.2. Проверка выносливости растянутой арматуры
1. Продолжаем расчет по блок-схеме 5.4. Все необходимые исходные
данные указаны выше.
2, 3.Определяем наибольшие и наименьшие напряжения σs,max и σs,min на
уровне растянутой арматуры:
 527, 7(0, 64 − 0, 04) 747,8 747,8 ⋅ 0, 6 ⋅ (0, 64 − 0, 04) 
σ s ,max = 5,538 
−
−
+
0, 0573
0,307
0, 0573


+ 0,9 ⋅ 0, 7 ⋅1120 ⋅ (1000) = 696,5 MПа.
 137,8(0,64 − 0,04) 747,7 747,7 ⋅ 0,6 ⋅ (0,64 − 0,04) 
σs,min = 5,538
−
−
+
0,0573
0,307
0,0573


+ 0,9 ⋅ 0,7 ⋅1120 ⋅ (1000) =672,7 MПа.
4. Определяем коэффициент асимметрии цикла:
ρs = σs,min/σs,max = 672,7/696,5= 0,96.
5. По таблице 1 Приложения 6 по линейной интерполяции определяем
коэффициент
γs4 =1. Так как растянутая арматура предварительно
напрягаемая – сварка не допускается, то коэффициент γs5 в расчете не
учитываем.
6. Проверяем выносливость растянутой арматуры:
σs,max = 696,5 < 1·1170=1170 МПа.
Условие удовлетворяется. Выносливость продольной рабочей арматуры
обеспечена.
5.4.3. Проверка прочности поперечной арматуры
Продолжаем расчет по блок-схеме 5.5.
1. При расчете на выносливость рассматривается работа только одного
крана, расположенного как показано на рис. 5.10.
2. Выносливость наклонных сечений проверяем на уровне центра тяжести
приведенного сечения. Поэтому определяем статический момент верхней
части сечения S’red:
S’red = 0,14·(1,2-0,64)2·0,5+(0,65-0,14)⋅0,16·(1,2-0,64-160/2)+
3
+ 6,153⋅226(560 - 40)+0 = 0,074м .
3, 4. Наибольшие и наименьшие касательные напряжения определяем по
формулам:
τ xy , max =
151 ⋅ 0,074
= 1451,1 kH/м 2 = 1, 45МПа;
0,055 ⋅ 0,14
48, 9 ⋅ 0,074
= 470 кН / м 2 = 0, 47 МПа. .
0, 055 ⋅ 0,14
5. Нормальные напряжения на уровне центра тяжести сечения не зависят
от внешней нагрузки и равны:
τ xy ,min =
σ x ,max = σ x ,min =
747,8
кН
= 2436 2 = 2,36 МПа.
0,307
м
Рис. 5.10. К расчету наклонных сечений на выносливость
6, 7. Определяем наибольшие и наименьшие главные растягивающие
напряжения:
2
σ mt ,max = −
2, 36
 2, 36 
2
+ 
 + 1, 36 = 0, 62 МПа;
2
2


2
2,36
 2,36 
2
+ 
 + 0, 47 = 0, 09МПа.
2
 2 
8. Коэффициент асимметрии цикла для поперечной арматуры равен:
σ mt ,min = −
ρs =
σ mt ,min
σ mt ,max
=
0, 09
= 0,145.
0, 62
9. По таблице 1 Приложения 6 для арматуры класса А400 определяем γs4
=0,43. Так как поперечная арматура приваривается к конструктивной
продольной арматуре точечной сваркой (поз. 1 обязательного приложение
3 СНиП 2.03.01-84*), по таблице 2 Приложения 6 при ρs = 0,145, классе
арматуры А - III (А400) и 2-й группе сварных соединений находим γs5 =
0,63.
Отсюда Rs = 0,43·0,63·355 = 96,2 МПа.
Проверяем условие 5.9 принимая Asw = 157 мм2 (2 ∅10) и As,inc = 0:
96, 2 ⋅157
σ mt ult =
= 0,36МПа < σmt,max = 0,62 МПа,
140 ⋅ 300
т.е. выносливость наклонных сечений не обеспечена. Необходимо
увеличить площадь поперечной арматуры, либо уменьшить их шаг s.
Проверяем условие 5.9, принимая Asw = 226 мм2 (2 ∅ 12) с шагом s = 200
мм и As,inc = 0:
96, 2 ⋅ 226
σ mt ult =
= 0, 77 МПа > σmt,max = 0,62 МПа,
140 ⋅ 200
Выносливость наклонных сечений обеспечена.
5.5. Расчет подкрановой балки по деформациям
Расчет по деформациям изгибаемого элемента, работающего без
трещин в растянутом бетоне, следует выполнять согласно п.4.21 [2].
С учетом приведенных выше данных, нормативная нагрузка от колеса
крана при коэффициенте k=1, определяется по формуле 5.5:
Pn = 0,95·235=223,25 кН.
1. Максимальный нормативный изгибающий момент от кратковременной
крановой нагрузки, согласно рис. 5.9, Мsh=790 кНм.
Изгибающий момент от продолжительного действия постоянных и
длительных нагрузок с учетом пониженного значения крановой
вертикальной нагрузки:
Мl = Mw,n +0,5Msh;
Мl = 137,5+395= 532,5кНм.
2. Модуль деформаций сжатого бетона при непродолжительном действии
нагрузок:
Eb1 = 0,85 E b =0,85·32500=27625 МПа.
3. Модуль деформаций сжатого бетона при продолжительном действии
нагрузок:
Eb
Ebτ1 =
;
1 + ϕb ,cr
где: φb,сr =2,3 - по таблице 1 Приложения 4 при заданной влажности
воздуха 50%.
Ebτ1 =
32500
= 9848, 48 МПа.
1 + 2, 3
4. Коэффициент приведения для К1400:
α=
Es 180000
=
= 6,52,
Eb1 27625
для стрежневой арматуры класса А400:
E
200000
αs = s =
= 7, 23.
Eb1 27625
5. Коэффициент приведения при учете длительных нагрузок:
E
α τ = τs ;
Eb1
180000
= 18,3.
9848,48
200000
α sτ =
= 20,3.
9848,48
6. Приведенный момент инерции сечения балки:
I red = 0, 053 + 7, 239 ⋅ 0, 000229 ⋅ (0, 64 − 0,12) +
ατ =
+6,52 ⋅ 0, 001060 ⋅ (0, 64 − 0, 04) + 7, 239 ⋅ 0, 000229 ⋅ (1, 2 − 0, 64 − 0, 04) = 0,059м 4 .
7. Приведенный момент инерции балки с учетом продолжительного
воздействия постоянных и длительных нагрузок:
τ
I red
= 0, 053 + 20, 3 ⋅ 0, 000229 ⋅ (0, 64 − 0,12) +
+20, 3 ⋅ 0,000229 ⋅ (1, 2 − 0, 64 − 0, 04) + 18, 3 ⋅ 0, 001060 ⋅ (0, 64 − 0, 04) = 0,0807м 4 .
8. Кривизна от непродолжительного действия кратковременных нагрузок:
M sh
1
;
  =
 r 1 Eb1 I red
790
1
1
= 0,00045536 .
  =
м
 r 1 27625000 ⋅ 0, 059
9. Кривизна продолжительного действия постоянных и длительных
нагрузок:
Ml
1
  = τ τ ;
 r  2 Eb1 I red
.
532,5
1
1
= 0,000669 .
  =
м
 r  2 9848480 ⋅ 0, 0807
10. Кривизна от непродолжительного действия усилия предварительного
обжатия:
Pe0 p
1
;
  =
 r 3 Eb1 I red
747,8 ⋅ 0, 6
1
1
= 0,000275 .
  =
м
 r 3 27625000 ⋅ 0, 059
11. Полная кривизна подкрановой балки:
1
1 1 1
  =   +  −  ;
 r  max  r 1  r  2  r 3
.
1
1
−4
  = ( 4,55+6,69-2,75 ) ⋅10 = 0,000849 .
r
м
  max
12. Расчетный прогиб балки составит:
1
f = Sl 2 ;
.
r
5
f = ⋅11,82 ⋅ 0, 000849 = 0, 0123=12,3 мм.
48
13. Так как
11800
f =12,3 мм < [
]= 29,5 мм.
400
Прогиб допустимый. Подкрановая балка удовлетворяет требованиям по
эксплуатационной пригодности.