Подготовка к ЕГЭ-4
реклама

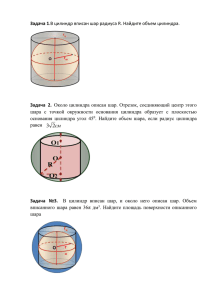
Подготовка к ЕГЭ - 3 Задачи по геометрии. № 1. Высота правильной треугольной пирамиды равна h, а двугранный угол при стороне основания равен 45 градусов. Найдите площадь поверхности пирамиды. DO=h, угол DKO=45º, 3-к DOK -прямоугольный и равнобедренный, т.к. угол ODK = 180-90-45 = 45° --> OK=OD=h. DK2= h2+h2; DK = h√2. OK - радиус вписанной окружности правильного 3-ка, значит стороны 3-ка равны a= 2r√3, т.е. AB = a = 2h√3. S осн = SABC = a2√3/4 = (2h√3)2√3/4 = 3h2 √3. SADB = AB*DK/2 = 2h√3*h√2 /2 = h2√6 Sполн = 3*SADB + Sосн = 3h2√6 +3 h2√3 =3 h2√3(√2+1) № 2. В прямоугольном параллелепипеде измерения равны 5 см, 8 см, 4√5см. Найдите угол между диагональю параллелепипеда и плоскостью его основания. Пусть а=8, b=4√5, c=5. d2= 8*8+(4√5)2 = 144 --> d=12. Искомый угол - / KOM - угол между диагональю ОК и ее проекцией ОМ. В 3-ке КОМ: КМ / ОМ = c / d = tg / KOM = 5/12. / KOM = arctg 5/12 Можно ответ выразить через синус. Найдем m. m2= d2 + c2 = 144 + 25 =169; d=13; c/m = 5/13 = sin / KOM / KOM = arcsin 5/13. Ответ: arcsin 5/13 № 3. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Найдите отношение объёма конуса к объёму шара. Пусть АВ=а, тогда АС=BС=а, R = a/2. Высота конуса = ОВ = √(BC2-OC2) = √(a2 - a2/4) = a√3/2 Vконуса = пR2*OB/3 = п a2/4*a√3/2 /3 = п a3√3/24 r - радиус шара. r=a√3 /6. Vшара = 4/3 *пr3 = 4/3* пa3 3√3 / 216 = пa3√3/54 Vконуса / Vшара = 54/24 = 2.25 Ответ: 2,25. № 4. Объем цилиндра 96π см3, площадь его осевого сечения 48 см². Найти площадь сферы, описанной около цилиндра. Ответ : S/π xy=48, y = 48/x. D - диагональ осевого сечения является диаметром шара. D2 = x2 + (48/x)2 ; S сферы =πD2. По условию V цил = 96π. V цил = πx2/4 *y = πx2/4*(48/x) = 12πх = 96π; x=96/12 = 6. D2=62 +(48/6)2 = 62+82 = 100. S сферы = πD2 = 100π. Ответ: 100. № 5. Радиус шара равен R. Найдите площадь поверхности вписанного в шар куба. Если куб вписан в шар, то его наибольшая диагональ D2 = 3a2 ; D2 = (2R)2 = 3a2 ; a2 = 4R2/3. S=6a2 = 6*4R2/3 = 8R2 Ответ: 8R2 № 6. Шар объёмом 6м3 вписан в цилиндр. Найдите объём цилиндра (в м3), описанного около шара. Диаметр шара D=2R, равен диаметру основания цилиндра и равен высоте цилиндра H. R - радиус шара и основания цилиндра. Vшара= 4/3 ∏R3 = 6. R3 = 4,5/∏ V цилиндра = ∏R2 ·H =∏R2 ·2R = 2∏R3 = 2∏·4,5 / ∏ = 9. Ответ: 9. № 7. В сферу вписан конус, образующая которого равна 1, а угол при вершине осевого сечения равен 60º. Найдите площадь сферы. S=4ПR2, где R - радиус сферы. Рассмотрим осевое сечение сферы. Оно представляет собой окружность, в которую вписан равнобедренный треугольник АВС с углом при вершине 60 градусов, углы при основании равны 60, значит этот треугольник равносторонний со стороной а. Радиус окружности, описанной около треугольника - это радиус сферы. По теореме синусов а/sin60=2R, где R - радиус окружности, описанной около треугольника , откуда R=a/√3 Тогда S=4ПR2=4Пa2/3 = 4П/3 Ответ: 4П/3 № 8. Стороны оснований и диагональ прямоугольного параллелепипеда относятся как 1:2:3. Длина бокового ребра равна 4. Найдите объем параллелепипеда. k - коэффициент пропорциональности, тогда а = k, b = 2k , d = 3k По формуле d2 = а2 + b2 + с2 находим стороны (3k)2 = k2 + (2k)2 + 42 d- диагональ, а, b, с - стороны параллелепипеда. 9k 2 = k2 + 4k2 + 16; 4k2=16; k=2; k=-2 не удовлетворяет условию: а=2, с=4. b=2*2=4, V= аbс = 2*4*4 = 32. Ответ: 32. № 9. Каким должен быть радиус основания цилиндра с квадратным осевым сечением, для того чтобы его объем был такой же, как и у шара радиуса 3м? Объем цилиндра равен Vц = πr2*h , где h-высота цилиндра, в нашем случае она равна h= 2r => Vц= 2πr3 Объем шара равен Vш = 4/3 πR3 , находим объем шара: Vш= 4/3 π*33 = 36π. Приравняем Vц = Vш и найдем r цилиндра 2πr3 = 36π; r3=18; r = 3√18 № 10. Чему равна полная поверхность конуса, описанного около правильного тетраэдра с ребрами длины а? Т.к. тетраэдр правильный, то в основание конуса вписан равносторонний треугольник со стороной a. R=a/√3. S боковой поверхности конуса Sбок.= πRL, где L=a, => Sбок.= πa2/√3 S полной поверхности конуса S= πa2/√3 + πa2/3 = πa2(1/√3+1/3) № 11. Чему равна площадь сферы, описанной около куба с ребром 1? По теореме Пифагора находим диагональ основания куба. Обозначим ее AD. AD2 = 12+12 = 2; Находим диагональ всего куба, она же - диаметр сферы. AD=√2 AC2 = AD2+DC 2= 2+12 = 3; AC = √3; Sсферы = 4πR2 = 4π*(3/4) = 3π. № 12. Найдите объем прямоугольной призмы, вписанной в цилиндр, если основание призмы служит прямоугольник, одна из сторон которого равна 6, радиус основания цилиндра 5 , высота призмы 10. Т.к. прямоугольник вписан в окружность, то его диагональ будет диаметром этой окружности, а также является гипотенузой прямоугольного треугольника, один из катетов которого равен 6. По теореме Пифагора найдем второй катет: x2 = (2*5)2 - 62 ; x=8 Найдем объем призмы: V=6*8*10=480 № 13 Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда. Решение. В основании параллелепипеда - квадрат. Его стороны равны диаметру основания цилиндра, т.е. а=d=2. V= Sосн·H = a2· H = 22·1=4. Ответ: 4. № 14. Прямоугольный параллелепипед описан около сферы радиуса 7,5. Найдите его объем. Решение. Если прямоугольный параллелепипед описан около сферы, то он - куб. Его ребра равны диаметру сферы, т.е. a = 7,5·2=15. V= a3 =153 = 3375. Ответ: 3375. № 15. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объём цилиндра, если объём конуса равен 27. Vцилиндра = Sосн H, Vконуса = Sосн H/3 =27. Видим, что объем конуса в 3 раза меньше объема цилиндра, значит Vцилиндра = Vконуса*3 = 27*3 =81. Ответ: 81. № 16. Шар объёмом 6 метров кубических вписан в цилиндр. Найдите объём цилиндра (в метрах кубических). V шара = (4/3)пR3 =6 --> R3 =6*3/(4п) = 4,5/п Vцил = пR2H = пR2*2R= 2пR3 = 2п* 4,5/п = 9 (м3) Ответ: 9. Замечание. Высота цилиндра, в который вписан шар, равна диаметру шара, а радиус основания цилиндра равен радиусу шара. № 17. В цилиндрический сосуд налили 200 cм3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь, при этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Выразить ответ в см3. Решение. Найдем площадь основания цилиндра. S=200/12=50/3. Если уровень воды поднялся на 9см, то объем воды с опущенной деталью увеличился на S*9=50/3*9=150 см куб. Это и есть объем детали. Ответ: 150. № 18. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба. Решение. Пусть ребро куба равно А, тогда V1=A·A·A, a V2=(A+1)(A+1)(A+1)=(A+1)3 = A3+3A2+3+1. Уравнение: V2–V1=19, (A3+3A2+3A+1) – A3 = 19, 3A2+3A-18=0, A2+A-6=0, A1=2, A2=-3 - не подходит. Чтобы решить, надо знать формулу (a+b)3 = a3 + 3a2b + 3ab2 + b3 Ответ: А=2 № 19. Закрытый сосуд в виде прямоугольного параллелепипеда с ребрами 30, 40, и 45 см стоит на горизонтальной поверхности таким образом, что наименьшая грань является дном. В сосуд налили воду до уровня 36 см. На каком уровне окажется вода, если сосуд поставить на наибольшую грань? (ответ дайте в см). Решение. V=30*40*36 - объем воды h – уровень воды 30*40*36 = 40*45*h V= 40*45* h, --> h=30*36/45 = 24 40*45 – наибольшая грань, Ответ: 24. № 20. С1. Диагональ правильной четырехугольной призмы равна L и наклонена с плоскости боковой грани под углом a, найти площадь боковой поверхности призмы. AB=L, угол BAC=a, угол BCA=90°, Sбок = 4x∙H Из 3-ка BAC: x=L sina, d=L cosa. Из 3-ка ACO: H=AO=√ (d2 - x2) = L√(cos2a - sin2a) = L√(cos2a). S = 4L2sina√ (cos2a) Ответ: 4L2sina√(cos2a)