КОНТРОЛЬНАЯ РАБОТА № 1 «Плоская система произвольно расположенных сил» Определить опорные реакции
реклама
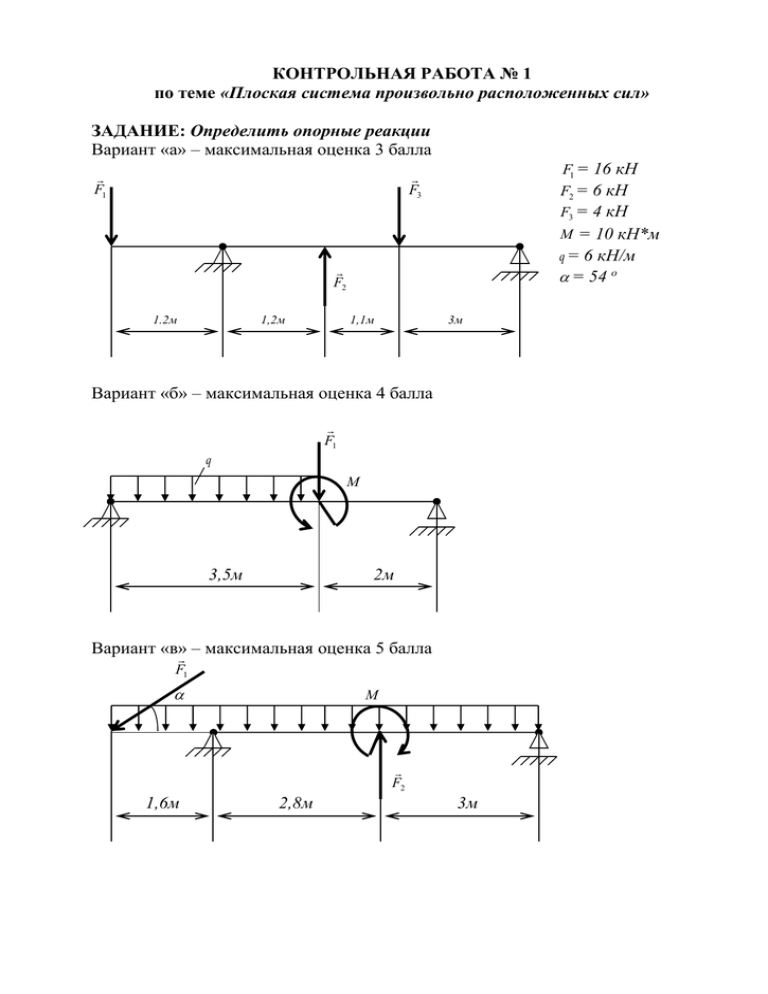
КОНТРОЛЬНАЯ РАБОТА № 1 по теме «Плоская система произвольно расположенных сил» ЗАДАНИЕ: Определить опорные реакции Вариант «а» – максимальная оценка 3 балла F1 = 16 кН F2 = 6 кН F3 = 4 кН F3 F1 M = 10 кН*м q= 6 кН/м = 54 о F2 1,2м 1.2м 1,1м 3м Вариант «б» – максимальная оценка 4 балла F1 q M 3,5м 2м Вариант «в» – максимальная оценка 5 балла F1 M F2 1,6м 2,8м 3м КОНТРОЛЬНАЯ РАБОТА № 1 по теме «Плоская система произвольно расположенных сил» ЗАДАНИЕ: Определить опорные реакции Вариант «а» – максимальная оценка 3 балла F3 F2 M F1 = 1,9 кН F2 = 2,3 кН F3 = 0,7 кН M = 3 кН*м q= F1 0,3м 0,7м 0,8м Вариант «б» – максимальная оценка 4 балла F3 F2 M q F1 0,3м 0,7м 0,8м Вариант «в» – максимальная оценка 5 балла F3 F2 q 300 F1 0,3м 0,7м M 0,8м 1,4 кН/м ПРИМЕРЫ РЕШЕНИЯ: Вариант «а» Определение опорных реакций балки на двух опорах при действии вертикальных нагрузок. у Дано: RA М F F = 50 кН М= 10кН*м RB х А В Определить: RA - ? RB - ? 2м 4м 2м 1. Обозначаем опоры А и В, проводим оси координат. 2. Отмечаем опорные реакции R A и R B . Горизонтальная составляющая в шарнирно-неподвижной опоре А равно 0, т.к. нагрузка только вертикальная. 3. Составляем уравнение равновесия для данной плоской системы параллельных сил. M A ( Fi) 0 M B ( Fi) 0 F * 2 M RB * 8 0 R A * 8 F * 6 M 0 4. Решаем систему уравнений. RB F *2 M 13.75 8 RA F *6 M 36.25 8 5. Выполняем проверку. F iy 0 RA – F + RB = 0 36.25 – 50 + 13.75 = 0 0=0 Реакции определены правильно. Вариант «б» Определение опорных реакций балки на двух опорах при действии вертикальных нагрузок. Дано: y RA RB F = 15 кН М= 5 кН*м q = 10 кН/м F М q х А В Определить: RA - ? RB - ? Fq 2м 1м 0,5м 2,5м 0,5м 1м 1. Заменяем распределенную нагрузку ее равнодействующей Fq = q * l =10 * 3 = 30кН, где l = 0,5 + 2,5 = 3м. Укажем расстояние от Fq до опор. 2. Обозначаем опоры А и В, проводим оси координат. 3. Отмечаем опорные реакции R A и R B . Горизонтальная составляющая в шарнирно-неподвижной опоре А равно 0. 4. Составляем уравнение равновесия для данной плоской системы параллельных сил. M A ( Fi) 0 M B ( Fi) 0 Fq *1 M RB * 3 F * 4 0 R A * 3 Fq * 2 M F *1 0 5. Решаем систему уравнений. RB RA Fq *1 M F * 4 3 30 *1 5 15 * 4 31.7кН 3 Fй * 2 M А *1 30 * 2 5 15 * 1 13.3кН 3 3 6. Выполняем проверку. F iy 0 RA + RB –Fq – F = 0 13.3 + 31.7 – 30 – 15 = 0 0=0 Реакции определены правильно. Вариант «б» Определение опорных реакций балки на двух опорах при действии произвольной нагрузки. у RA Дано: RA у F RB М q 45 х 0 А RA x F = 30 кН М= 15 кН*м q = 10 кН/м В Определить: Fq 2м 3м 5м 2м RA - ? RB - ? 1. Обозначаем опоры А и В, проводим оси координат. 2. Заменяем распределенную нагрузку ее равнодействующей Fq = q * l =10 * 2 = 20 кН. Укажем расстояние от Fq до опоры А. 3. Отмечаем опорные реакции RAy , RAx , RB . RA RAy RAx 2 2 4. Составляем уравнения равновесия. Решаем их, выполняем проверку. Fix 0 M A ( Fi) 0 M B ( Fi) 0 Проверка: Fiy 0 R Ax F * cos 45 0 0 0 Fq *1 F * cos 45 * 3 RBy * 8 M 0 0 M F * 5 * cos 45 R Ay * 8 Fq * 9 0 F * cos 450 Fq RAy RDy 0 R Ax F * cos 45 0 21кН RB у RA y Fq *1 F * cos 45 0 * 3 M 8 3.5кН M F * 5 * cos 45 0 Fq * 9 А *1 8 37.5кН -30 * 0.7 – 20 + 37.5 + 3.5 = 0 0=0 Задача решена верно 5. Находим реакцию R A : R A 212 37.5 2 42.9кН





