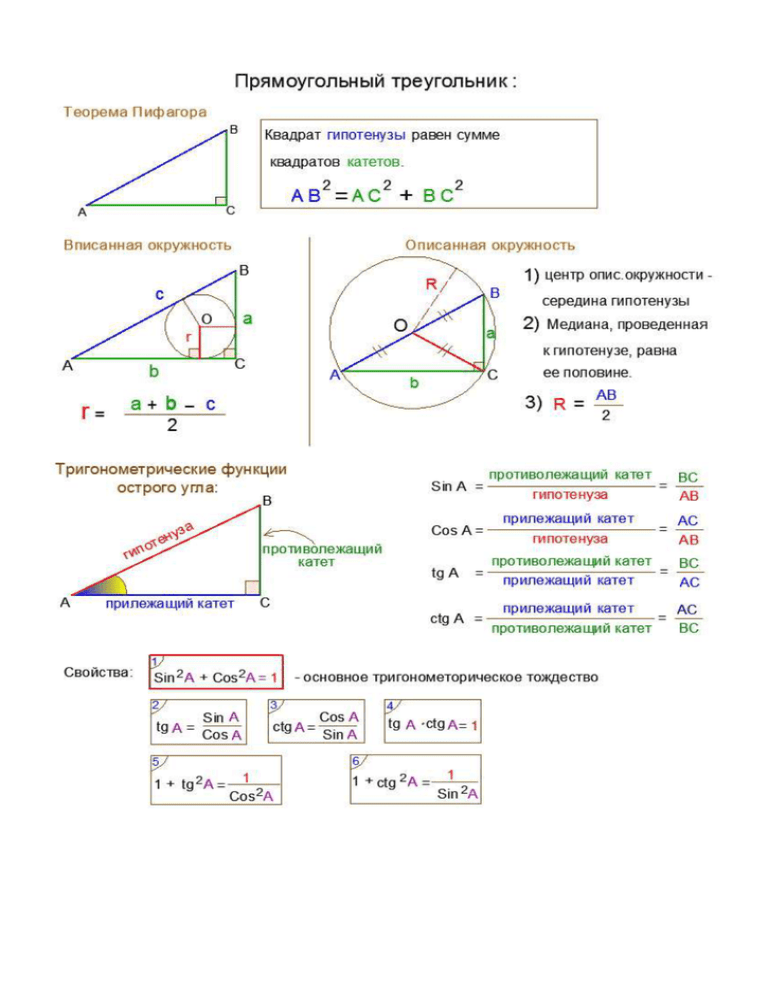
Для решения задач по геометрии части В и задания С4
реклама
Свойства медиан в треугольнике: 1) Все медианы пересекаются в одной точке и делятся в этой точке в отношении 2:1, считая от вершин. 2) Каждая медиана делит треугольник на две равновеликие части (с равными площадями). 3) Все медианы треугольника делят его на 6 равновеликих треугольников Свойства биссектрис в треугольнике: 1) Все биссектрисы пересекаются в одной точке (центр вписанной окружности) 2) а) Каждая биссектриса делит противолежащую сторону на отрезки, пропорциональные к прилежащим сторонам. Свойство серединных перпендикуляров к сторонам треугольника: 1) Все серединные перпендикуляры в треугольнике пересекаются в одной точке – центре описанной окружности 2) Каждая точка серединного перпендикуляра, проведенного к стороне треугольника равноудалена от ее концов. 3) На рисунке луч BP – биссектриса угла ABC Для доказательства подобия треугольников можно использовать следующие признаки: 1) По двум углам: если два угла одного треугольника равны соответственно двум углам другого, то треугольники подобны 2) По двум пропорциональным сторонам и углу между ними: если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны. 3) По трем сторонам: если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то треугольники подобны. Материалы сайта «Профессиональный репетитор по математике» www.ankolpakov.ru Колпаков Александр Николаевич. 8-916-081-68-55 Индивидуальные занятия по математике в Москве. Подготовка к ЕГЭ, Подготовка в МГУ, подготовка к ГИА, олимпиадная помощь.











