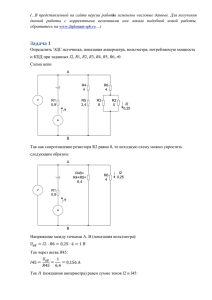
Задача № 6.
реклама

(...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Задачи по теории вероятности. СОДЕРЖАНИЕ Задача № 6. ................................................................................................................? Задача №?9. .............................................................................................................. 6 Задача № ?? .............................................................................................................. 7 Задание №? .............................................................................................................. ?? 2 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Задача № 6. На сборку поступило десять деталей, среди которых четыре бракованные. Сборщик наудачу берет три детали. Найти вероятность событий: 1. Все взятые детали стандартные; 2. Только одна деталь среди взятых стандартная; 3. Хотя бы одна из взятых деталей стандартная. Пункт ?. Все взятые детали стандартные: Решение: Обозначим события: А – все взятые детали стандартные; А? – только одна из взятых деталей стандартная; А? - ? детали стандартные; А? – все взятые детали нестандартные. По определению суммы событий – искомое событие: А = А? + А? +А? События А?, А?, А? несовместимы, следовательно: Р(А) = Р(А? + А? +А?) = Р(А?) + Р(А?) +Р(А?) Пространство элементарных событий будут образовывать неупорядоченные последовательности деталей, отличающиеся друг от друга хотя бы одной деталей. Число таких последовательностей вычисляется по формуле: r ! k !*( r k )! k C r В задаче ?? деталей. При вычислении общего числа элементов пространства элементарных событий k=? (выбираются случайно ? детали), т.е: 3 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) 3 n C10 Определим число элементов, благоприятствующих событию А? : одну качественную деталь можно выбрать только из качественных деталей, т.е. 1 способами C 6 Некачественные ? детали выбирается из 6 деталей, т.е и поскольку к любой из C2 4 способами; C16 деталей может присоединиться любая из деталей, общее число возможных последовательностей 1* 2 m 1C 6 C 4. Таким образом: 6 ! 4 ! 720 24 * * 1 2 * C C 6 * 6 * 3024 1 !* 5 ! 2 !* 2 ! 1 * 120 2 * 2 6 4 P 0 . 3 A 1 3 10 ! 3628800 36288 C 10 3 !* 7 ! 6 * 5040 Аналогичным образом получим Р(А?) и Р(А?): 6 ! 4 ! 720 24 * * 2 1 * C C 15 * 4 * 3024 2 !* 4 ! 1 !* 3 ! 2 * 24 1 * 6 6 4 P 0 . 5 A 2 3 10 ! 3628800 36288 C 10 3 !* 7 ! 4 ! 30240 24 3 C 4 3 !* 1 ! 4 P 6 0 . 033 A 3 3 10 ! 3628800 3628800 C 10 3 !* 7 !6 * 5040 30240 Окончательный результат Р(А) = Р(А?) + Р(А?) +Р(А?) = ?.? + ?.? + ?.??? = ?.8?? Пункт ?. Только одна деталь среди взятых стандартная Решение: Обозначим события: А – только одна из взятых деталей стандартная; А? – ? бракованная и две качественные; А? – все бракованные ; 4 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) А? – все взятые детали стандартные. 4 ! 6 ! 24 720 * * 1 2 * C C 4 * 15 * 3024 1 !* 3 ! 2 !* 4 ! 1 * 6 2 * 24 4 6 P 0 . 5 A 1 3 10 ! 3628800 36288 C 10 3 !* 7 ! 4 ! 6 * 5040 24 3 C 4 3 !* 1 ! 4 P 6 0 . 033 A 2 3 10 ! 3628800 3628800 C 10 3 !* 7 !6 * 5040 30240 6 ! 720 3 C 6 !* 5 ! 120 61 P 0 . 005 A 3 3 10 ! 3628800 3628800 C 10 3 !* 7 !6 * 5040 30240 Окончательный результат Р(А) = Р(А?) + Р(А?) +Р(А?) = ?.? + ?.??? + ?.?? = ?.?8? Пункт ?. Хотя бы одна из взятых деталей стандартная Решение: Обозначим события: А – хотя бы одна из взятых деталей стандартная; А? – все бракованные; А? - две из взятых деталей стандартная и одна бракованная; А? – все взятые детали стандартные. 4 ! 24 3 C 4 3 !* 1 ! 4 P 6 0 . 033 A 1 3 10 ! 3628800 3628800 C 10 3 !* 7 !6 * 5040 30240 4 ! 6 ! 24 720 * * 1 2 * C C 4 * 15 * 3024 1 !* 3 ! 2 !* 4 ! 1 * 6 2 * 24 4 6 P 0 . 5 A 2 3 10 ! 3628800 36288 C 10 3 !* 7 ! 6 ! 6 * 5040 720 3 C 20 !* 3 ! 63 P 3 36 0 . 166 3 10 ! 3628800 3628800 C 10 3 !* 7 !6 * 5040 30240 5 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Окончательный результат Р(А) = Р(А?) + Р(А?) +Р(А?) = ?.??? + ?.? + ?.?66 = ?.699 Задача №?9. Математическое ожидание случайной величины, распределенной по нормальному закону, равно -?, а вероятность попасть в интервал |η+?| < ? равна ?,?. Найти ее дисперсию; построить кривую вероятности; вычислить вероятности событий: 1. случайная величина примет значение больше чем m+σ 2. случайная величина примет отрицательное значение. Решение: Формула для вычисления дисперсии: 2 2 D M M D 4 2 2 Среднее квадратическое отклонение: D 1 .4142 η принадлежит интервалу ]-6;?[ (из условия задачи |η+?| < ?). Плотность вероятности случайной величины: ? при х > -6 f(x) = ?.? при -6 < х < -? ? при х > -? Функция распределения: F(x) = ? при х < ? 6 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) ?.?х? при -6 < х < -? ?.9??? при х > -? Плотность вероятности x -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 0 -0,5 f(x) -1 -1,5 -2 -2,5 -3 Задача № ?? Прибор состоит из двух независимо работающих блоков А и В, каждый из которых состоит из нескольких элементов. Вероятности отказов каждого из элементов: Р? = ?.?, Р? = ?.?, Р? = ?.?, Р? = ?.?, Р? =?.?, Р6 =?.?, Р7 =?.?. При отказе блока он подлежит полной замене, причем стоимость замены блока А составляет С? = ?, блока В – С? = 8 единиц стоимости. Предполагается, что за период времени Т замененный блок не выйдет из строя еще раз. Найти: ?. Найти случайную величину η – стоимость восстановления прибора за период времени Т. ?.?. построить ее ряд и функцию распределения. ?.?. вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение. 7 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) ?. Построить модель найденной случайной величины для двадцати приборов (методом жребия получить ее ?? значений). ?.?. Найти экспериментальный ряд и функцию распределения. ?.?. Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения. ?.?. Построить графики теоретических и экпериментальных ряда и функции распределения. ?. С помощью критерия Пирсона оценить соответствие экспериментального распределения теоретическому с уровнем значимости α = ?.??. А. В. 4 1 2 5 6 7 3 Решение: Случайная величина η - «стоимость ремонта» может принимать только четыре значения. 1. х? = ? – ни один блок не потребует замены; 2. х? = С? = ? – только блок А потребует замену; 3. х? = С? = 8 – только блок В потребует замену; 4. х? = С? + С? = ?? – оба блока потребует замену. Чтобы вычислить вероятность каждого из значений следует сначала найти вероятность выхода из строя блоков А и В. 8 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Обозначим А – выход из строя блока А, Аi – отказ i – элемента ( i = ?,?,6,7). Блок А откажет если откажет хотя бы одна из его частей или все его части. По определению суммы событий: А = А? + А? + А? В силу теоремы сложения вероятностей совместных событий: Р(А) = Р(А? + А? + А?) = Р(А?) + Р(А?) + Р(А?) В силу независимости событий Аi получим: Р(А) = Р(А?) * Р(А?) * Р(А?) + Р(А?) + Р(А?) + Р(А?) - Р(А?) * Р(А?) * Р(А?) = ?.? * ?.? * ?.? + ?.? + ?.? + ?.? – ?.? * ?.? * ?.? = ?.6?6 – ?.??6 = ?.6 Определим вероятность того, что блок А не откажет за время Т (событие A) Р( A ) = ? – Р(А) = ? – ?.6 = ?.???? Обозначим В – выход из строя блока В, Вi – отказ i – элемента ( i = ?,?,?). Блок В откажет если откажет хотя бы одна частей ветви ?,6,7 или элемент ?, или все его части. По определению суммы событий: В = В?В6В7 + В? В силу совместности и независимости событий вероятность события Ы определяется формулой: Р(В) = Р(В?)Р(В6)Р(В7) + Р(В?) - Р(В?)Р(В6)Р(В7)Р(В?) Таким образом Р(В) = ?.? * ?.? * ?.? + ?.? – ?.? * ?.? * ?.? * ?.? = ?.???? – ?.???? = ?.???? Найдем вероятность безотказной работы блока В: Р( B ) = ? – Р(В) = ? – ?.? = ?.9??? Найдем вероятности значений случайной величины η. 9 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Случайная величина имеет значение х? = ?, если произойдет событие * A B ( оба блока исправны за время Т). Эти события независимы, поэтому: Р(η=?) = Р( A ) * Р( B ) = ?.???? * ?.9??? = ?.?6?? Значение х? = ? принимается, если отказывает блок А и не отказывает блок В, т.е.: Р(η=?) = Р(А) * Р( Р(η=8) = Р( B ) = ?.6??? * ?.9??? = ?.???? A В) = ?.???? * ?.???? = ?.???? Р(η=??) = Р(АВ) = ?.6??? * ?.???? = ?.?6?? Сведем полученные результаты в табл.?, которая будет являться рядом распределения случайной величины η. Таблица ? xi ? ? 8 ?? сумма pi ?,?6 ?,?? ?,?? ?,?6 ? Построим многоугольник распределения: по оси абсцисс откладываются значения случайной величины хi, по оси ординат значения их вероятностей рi. 10 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Многоугольник распределения 0,6 0,5 Рi 0,4 0,3 Значения Х 0,2 0,1 0 0 4 8 12 Хi Найдем функцию распределения случайной величины, используя соотношение: F (x) p i xi x При х < ? F(x) = ? При ? ≤ х < ? F(x) = P(η=x?) = p?= ?.?6?? При ? ≤ х < 8 F(x) = P(η=x?)+ P(η=x?)= p? + p?= ?.9??? При 8 ≤ х < ?? F(x) = P(η=x?)+ P(η=x?)+ P(η=x?) = p? + p? + p? = ?.9??? При х ≥ ?? 4 F ( x ) P ( ) 1 . 0000 x i i 1 Таким образом: ? при х < ? ?.?6?? при ? ≤ х < ? F(x) = ?.9??? при ? ≤ х < 8 ?.9??? при 8 ≤ х < ?? ?.??? при х ≥ ?? 11 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) Построим график функции распределения: Функция распределения 1,2 1 F(x) 0,8 0,6 0,4 0,2 0 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Xi Найдем математическое ожидание M[η], дисперсию D[η] и среднее квадратичное отклонение ση исследуемой случайной величины, используя формулы: n M x ip i i 1 2 2 D M M D Результаты вычислений сведем в таблицу: xi ? ? 8 ?? сумма pi ?,?6 ?,?? ?,?? ?,?6 ? xi*pi ? ?,?6 ?,?? ?,7? M[η] = ?,???? xi?*pi ? 8,6? ?,?6 8,6? M[η?] = ?9,8??? (M[η])? = ??,???? 12 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) D[η] = 9,6??? ση = ?,?98? Вывод: Случайная величина «стоимость ремонта» имеет среднее значение ?.? денежных единицы со среднеквадратическим отклонением ?.?98?. Дискретная случайная величина задана рядом распределения: xi ? ? 8 ?? сумма pi ?,?6 ?,?? ?,?? ?,?6 ? Для рассматриваемой случайной величины правило моделирования примет вид: Интервал zi ? ?;?.?6? ? ? ?.?6?;?.9? ? ? ?.9?;?.9?? 8 ? ?.9??;?.??? ?? Для моделирования возьмем число η из табл. №? (методические указания). Начнем с ?? строки 8 столбца. j ri интервал zi j интервал zi ?,? ?.?6?;?.9? ?,? ?.?6?;?.9? ? ri ? ?,?? ?;?.?6? ? ?? ? ?,? ?;?.?6? ? ?? ?? ?? ?,?7 ? ?,9? ?.9??;?.??? ?,?? ?.?6?;?.9? ? ?? ? ?,?8 ?.?6?;?.9? ? ?? ?,?9 ?.?6?;?.9? ?,98 ?.?6?;?.9? 6 ?,6 ?.?6?;?.9? ? ?6 ?? ?7 8 ?,97 ?.9??;?.??? ?;?.?6? ?,?9 ?,? ?.?6?;?.9? ?,7? ?.?6?;?.9? ? ?8 ?,?6 9 ?,?? ? ?9 ?,8? ?.?6?;?.9? ? 7 ?;?.?6? ?;?.?6? ?;?.?6? ? ? ? ?? ? ? ? ? 13 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) ?? ?;?.?6? ? ?;?.?6? ? ?? ?,?? ?,?8 Найдем экспериментальный ряд распределения. Для этого подсчитаем частоты mi, равные числу приборов с данной стоимостью ремонта, т.е. числу появлений xj, вычислим их относительные частоты. xi ? ? 8 ?? сумма mi 7 ?? ? ? ?? ?,?8 ?,? ?,?? ?,?8 pi Найдем экспериментальную функцию распределения: ?,8 * * p F i xxi ? при х < ? ?.?8?? при ? ≤ х < ? ?.68?? при ? ≤ х < 8 F*(x) ?.7??? при 8 ≤ х < ?? ?.8?? при х ≥ ?? Прямоугольник распределения 0,5 0,4 pi 0,3 0,2 0,1 0 0 1 2 3 xi Найдем оценки числовых характеристик: Математическое ожидание: 14 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) k * m x ip i i 1 Дисперсия: * * D D несм смещ n n 1 Вычисления сведем в таблицу: xi p* i * x i pi * x i2 pi ? ?.?8 ? ?.? 8 ?.?? ?? ?.?8 сумма ?.8 ? ?,6 ?,???6 ?,???8 m*=?,6?6? ? 6,? ?,?6 ??,?? M*[η?]=??,?8 (m*)? = ?,?8???? ?7,899?8 D*[η]смещ = * * 17 . 899 18 . 841 D несм 20 20 1 * 4 . 340 D несм Проверим соответствие закона распределения полученной случайной величины F*(х) заданному закону распределения F(x) используя критерий Пирсона. Для этого определяется случайная величина: 2 km np i 2 i 1 i np i где k – число значений случайной величины; mi – число появлений значений случайной величины η; pi – теоретическая вероятность значения; 15 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) n – объем моделируемой выборки. Величина χ? называется «хи-квадрат», служит показателем того, насколько хорошо согласуется моделируемое и ожидаемое распределения. В рассматриваемой задаче число k=? , число l=?. По таблице ? (методические указания) найдем критические числа С? (для α?=?.??) и С? (для α?=?.??). Ими являются ??.? и 7.8. Найдем значения χ?. mnp2 i i xi mi npi ? ? 7 ?,6 ? ? ?? 8 ? 8 ? ? ?? ? Σ - ?? mi-npi i npi ?,? ?,?? ? ?,? ?,8 ?,? ?,?? ?,6 ?6 ?,? ?,? ? χ?=? Вывод: При уровне значимости α?=?.?? событие χ? > C? (?<7.8) не произошло – полученное распределение не противоречит предполагаемому. При менее жестких условиях (α?=?.?? ) событие χ? > C? (?<??.?) тем более не произошло, и в этом случае можно считать, что гипотеза о распределении случайной величины с заданным законом распределения не противоречит смоделированным значениям случайной величины. Задание №? По выборке объемом n=?? вычислены оценки математического ожидания m* = -? и дисперсия s? = ?.?. При заданной доверительной вероятности β = ?.999 найти предельную ошибку оценки математического 16 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) ожидания и доверительный интервал. Определить какими будут эти величины, если при выборке объемом n=?? получены такие же величины оценок. Решение: Математическое ожидание m и дисперсия σ? не известны, поэтому воспользуемся формулами: t s n s s n n * * * * ( ; ) ( ; ) t t l m m m m где ε – предельная ошибка; lβ – доверительный интервал, соответствующий доверительной вероятности β; tβ – значение квантиля распределения Стьюдента для числа степеней свободы k = n – ?. В данном случае k = ?9, а доверительная вероятность β = ?.999. По таблице ?? (методические указания) находим tβ = ?.88???. Тогда предельная ошибка: s 0 . 4 0 . 6324 3 . 88332 3 . 88332 0 . 5634 t 4 . 3588 n 19 Найдем доверительный интервал: s s * * ( ; ) ( 3 0 . 5634 ; 3 0 . 563 ) ( 3 . 56 ; 2 . 43 ) t t l m m n n Полученный результат позволяет утверждать, что с вероятностью ?.999 математическое ожидание рассматриваемой случайной величины принадлежит интервалу (-?.?6??; -?.??6?). 17 (...В представленной на сайте версии работы изменены числовые данные. Для получения работы с корректными величинами, обратитесь на www.diplomant-spb.ru ...) При выборке ?? элементов воспользуемся формулами для вычисления предельной ошибки оценки математического ожидания: z n и формулой для вычисления доверительного интервала: n n * * * * ( ; ) ( ; ) l m m m z m z В этих формулах zβ находится как корень уравнения 1 Ф (z ) 2 по таблицам значений нормированной функции нормального распределения. Zβ = (?+?.999) / ? = ?.999? Входим с этим значением в таблицу и находим ее аргумент, равный = ?.?7. Таким образом: 0 . 4 0 . 6324 3 . 27 3 . 27 0 . 327 z 6 . 3245 n 40 Доверительный интервал равен: * * ( ; ) ( 3 0 . 327 ; 3 0 . 327 ) ( 3 . 32 ; 2 . 67 ) l m z m z 0 . 999 n n 18