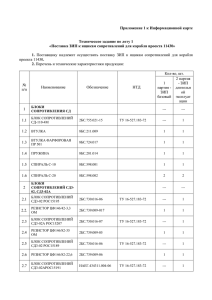
N-звенная цепочка сопротивлений (конденсаторов и т.П.)

УДК 004.4(06) Информатика и процессы управления
Л.B. ТУПИКИНА
Научный руководитель – Д.В. ХРАМЧЕНКОВ
ГОУ лицей 1511 при МИФИ
N-ЗВЕННАЯ ЦЕПОЧКА СОПРОТИВЛЕНИЙ
(КОНДЕНСАТОРОВ И Т.П.) КАК ДИНАМИЧЕСКАЯ
СИСТЕМА
Рассмотрены N-звенные цепочки сопротивлений, для которых расчет величины сопротивления можно
представить в графическом виде, подобном изображенному на рисунке, или в виде точечных отображений
типа
(1)
R n 1  f  (R n ) , n=1, 2, 3, ...,
где R (приложенное напряжение и т.п.) и α – некоторые числовые параметры. Случаю бесконечной цепочки
сопротивлений отвечает неподвижная точка отображения (1).
R1
R2
R n
= R n 1
Нас интересовали случаи возникновения в подобных системах периодических и хаотических режимов.
До сих пор периодические и хаотические режимы в бесконечных цепочках, составленных из индуктивностей, конденсаторов и т.п., представляли собой особенности возбуждения, электрического передаваемого со
временем из одного звена цепочки в соседнее. В нашем случае такие режимы представляли бы собой изменение сопротивления или иной характеристики цепи при добавлении к ней еще одного аналогичного звена.
Мы провели анализ устойчивости неподвижной точки отображения (1) В случае, когда рассматриваемая
цепочка состояла из обычных сопротивлений (или конденсаторов, или э.д.с. с сопротивлениями) при весьма
различных топологических моделях цепи, неподвижная точка оказалась устойчивой независимо от параметров ее элементов. Однако если элементы цепи дополнить также диодами (идеальными и неидеальными), то
ситуация изменяется. В случае цепи, составленной из сопротивлений, добавление неидеальных диодов можно рассматривать как переход от линейных сопротивлений к нелинейным. А именно, мы предположили, что
неидеальный диод имеет нулевое сопротивление по отношению к прямому току, при значениях тока или
напряжения, меньше критического его обратное сопротивление равно бесконечности, а при больших критического значения – конечному сопротивлению, тогда сопротивление вместе с параллельно подсоединенным
к нему диодом можно считать нелинейным: R  r1 при I  I кр , R  r2 при I  I кр . Для второго элемента цепочки, изображенной на рисунке, мы предположили пороговую зависимость сопротивления от приложенного ко входу напряжения R2=p1 при U<Uкр,R2=p2 U>=Uкр. В этом случае поведение цепочки сопротивлений зависит от приложенного ко входу напряжения. Найдены параметры, при которых неподвижная
точка соответствующего отображения становится неустойчивой. Установлено, что это отвечает периодическому режиму. Построена аналогичная по поведению цепочка из э.д.с., линейных сопротивлений и идеальных диодов.