решения заданий Олимпиады по физике

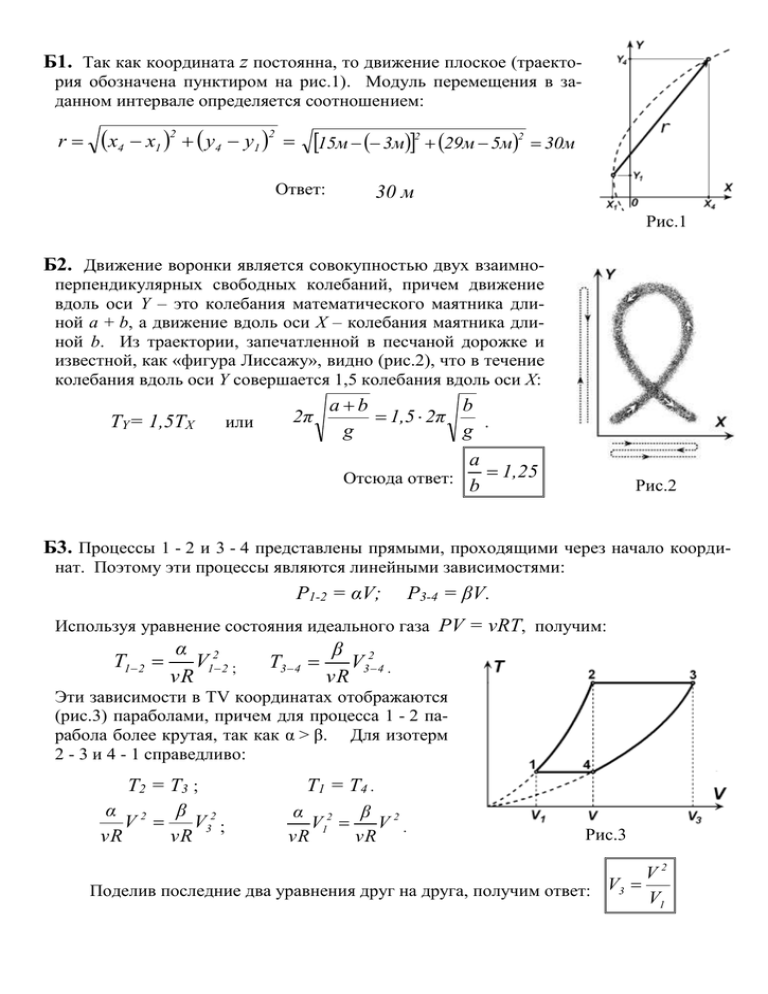
Б1. Так как координата z постоянна, то движение плоское (траектория обозначена пунктиром на рис.1). Модуль перемещения в заданном интервале определяется соотношением:
r
x4  x1 2   y4  y1 2
15м   3м2  29м  5м2  30м

Ответ:
30 м
Рис.1
Б2. Движение воронки является совокупностью двух взаимноперпендикулярных свободных колебаний, причем движение
вдоль оси Y – это колебания математического маятника длиной a + b, а движение вдоль оси Х – колебания маятника длиной b. Из траектории, запечатленной в песчаной дорожке и
известной, как «фигура Лиссажу», видно (рис.2), что в течение
колебания вдоль оси Y совершается 1,5 колебания вдоль оси Х:
ТY= 1,5ТX
или
2π
ab
b
 1,5  2π
.
g
g
a
Отсюда ответ: b  1,25
Рис.2
Б3. Процессы 1 - 2 и 3 - 4 представлены прямыми, проходящими через начало координат. Поэтому эти процессы являются линейными зависимостями:
P1-2 = αV;
P3-4 = βV.
Используя уравнение состояния идеального газа РV = νRT, получим:
T1 2 
α 2
V1 2 ;
νR
T3  4 
β 2
V3  4 .
νR
Эти зависимости в ТV координатах отображаются
(рис.3) параболами, причем для процесса 1 - 2 парабола более крутая, так как α > β. Для изотерм
2 - 3 и 4 - 1 справедливо:
Т2 = Т 3 ;
α 2
β
V  V32 ;
νR
νR
Т1 = Т4 .
α 2
β
V1  V 2 .
νR
νR
Рис.3
V2
Поделив последние два уравнения друг на друга, получим ответ: V3  V
1
Б4. Пусть при горизонтальном положении цилиндра объем каждой из половин был V.
При вертикальном положении объем верхней части стал V+v и давление в ней р1, а
mg
объем нижней части V-v и давление в ней p1 
. Согласно закону БойляS
Мариотта для верхней и нижней частей имеем:
рV = р1(V+v),
mg 

pV   p1 
V  v  .
S 

После деления уравнений на V имеем:
v

p  p1  1  
 V
mg 
v

p

p

1




.
1
и
S  V 

v
Исключив из этих уравнений неизвестную величину
, получим квадратное уравнеV
mg 
mgp

2
p

p

p

 0, из которого найдем


1
ние 1
S 
2S

1
mg
 mg 
2
p
p


p



1
ответ:
2
S
S



(второй корень отброшен, так как он дает для р1 отрицательное значение).
2




Б5. Со стороны электрического поля на заряженный шарик
действует сила Еq (рис. 4), придающая ему, в соответствии со
Eq
2 законом Ньютона, горизонтальное ускорение a x 
.
m
Тогда, по истечении промежутка времени t, координата х шаРис.4
2mx
a x t 2 Eqt 2
2
t


. Отсюда
рика равна x 
Eq .
2
2m
Изменение координаты y шарика обусловлено его свободным падением под действиgt 2 mg
y

x
ем силы тяжести с ускорением g:
2
Eq .
mg
y

x
Ответ:
Eq .
Б6. По завершении процесса заряда конденсаторов ток прекращается, и тогда все конденсаторные пластины, соединенные с резистором, будут иметь одинаковый потенциал. Емкости С + С1 и С + С2 включены с источником последовательно. Общее падение напряжения на них равно
U1 + U2 = Е ,
а заряд на их пластинах
Рис.5
q = (С + С1)U1 = (С + С2)U2 .
E(C  C2 )
U

1
Решив эти уравнения, получим ответ:
2C  C1  C2
U2 
E(C  C1 )
2C  C1  C2
Б7. Если резистор подключен к сети переменного тока без выпрямительного диода, то
U2
P
выделяемая в резисторе мощность
, где U – действующее (эффективное)
R
напряжение в сети. Если резистор подключен к сети через диод, то в резисторе выде-
U2
ляется мощность в 2 раза меньше: P1 
.
2R
Подключение конденсатора приводит к его заряжанию до амплитудного значения
напряжения U0 в сети.
U 02 ( 2U ) 2 2U 2


Тогда P2 
R
R
R
.
Следовательно
P2
 4.
P1
Ответ: Замыкание ключа приводит к 4-х кратному увеличению выделяемой в резисторе тепловой мощности.
Б8. Ход лучей в пластине показан на рис.6. В прямоугольном
треугольнике АВС сторона АВ = L / cosα,
а в треугольнике АВD сторона АВ = 2d tgβ.
По закону преломления sinα / sinβ = n.
Решив совместно эти уравнения, получим после исключения
2
неизвестных β и АВ ответ:
 d

n  sinα 1   2 cosα   1,8.
 L

Рис.6
Б9. Поскольку создаваемое линзой изображение удалено от нее на расстояние большее, чем фокусное расстояние, то эта линза собирающая. Далее возможны 2 случая.
1) Изображение действительное. На
рисунке 7 обозначены: h – высота предмета, H – высота изображения, f –
фокусное расстояние.
Из подобия треугольников следует:
h
f

H 2f
Тогда H = 2h = 4 см.
.
Рис. 7
2) Изображение мнимое. Из подобия
треугольников на рис. 8 следует:
h
f

H 4f
.
Ответ:
Тогда H = 4h = 8 см.
1) 4 см; 2) 8см.
Рис. 8