Урок 10. Показательные уравнения. Показательная функция

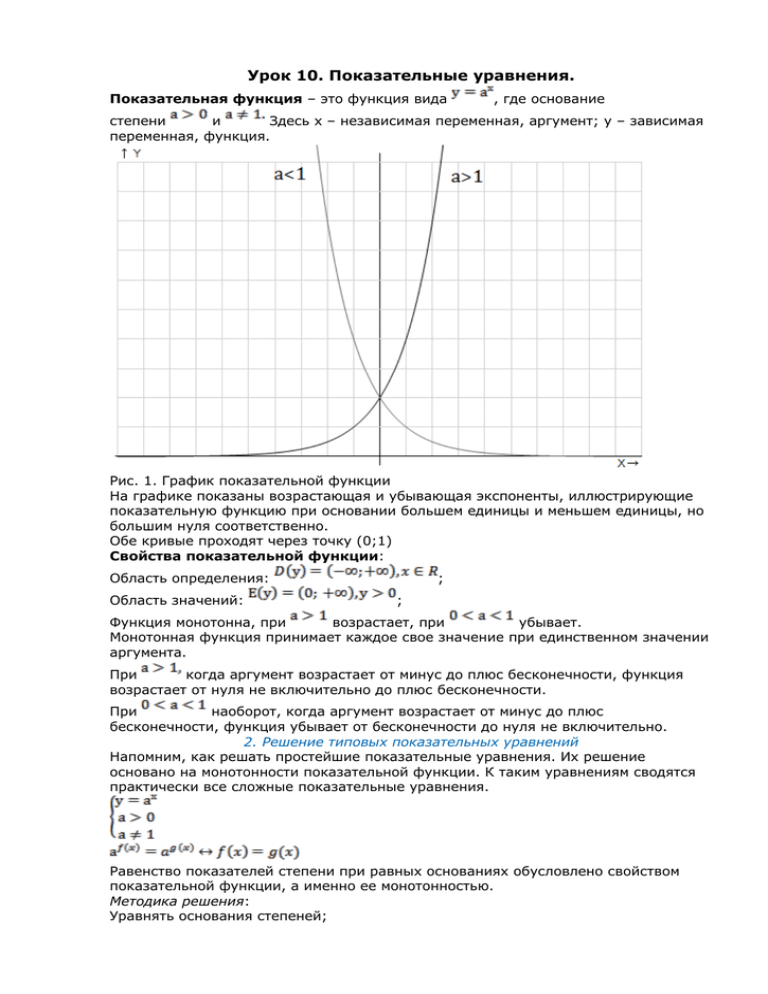
Урок 10. Показательные уравнения.
Показательная функция – это функция вида
, где основание
степени
и
Здесь х – независимая переменная, аргумент; у – зависимая
переменная, функция.
Рис. 1. График показательной функции
На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие
показательную функцию при основании большем единицы и меньшем единицы, но
большим нуля соответственно.
Обе кривые проходят через точку (0;1)
Свойства показательной функции:
Область определения:
Область значений:
;
;
Функция монотонна, при
возрастает, при
убывает.
Монотонная функция принимает каждое свое значение при единственном значении
аргумента.
При
когда аргумент возрастает от минус до плюс бесконечности, функция
возрастает от нуля не включительно до плюс бесконечности.
При
наоборот, когда аргумент возрастает от минус до плюс
бесконечности, функция убывает от бесконечности до нуля не включительно.
2. Решение типовых показательных уравнений
Напомним, как решать простейшие показательные уравнения. Их решение
основано на монотонности показательной функции. К таким уравнениям сводятся
практически все сложные показательные уравнения.
Равенство показателей степени при равных основаниях обусловлено свойством
показательной функции, а именно ее монотонностью.
Методика решения:
Уравнять основания степеней;
Приравнять показатели степеней.
Перейдем к рассмотрению более сложных показательных уравнений, наша цель –
свести каждое из них к простейшему.
Пример 1:
Освободимся от корня в левой части и приведем степени к одинаковому
основанию:
Для того чтобы свести сложное показательное уравнение к простейшим, часто
используется замена переменных.
Пример 2:
Воспользуемся свойством степени:
Вводим замену. Пусть
, тогда
. При такой замене очевидно,
что у принимает строго положительные значения. Получаем:
Умножим полученное уравнение на два и перенесем все слагаемые в левую часть:
Первый корень не удовлетворяет промежутку значений у, отбрасываем его.
Получаем:
Пример 3:
Приведем степени к одинаковому показателю:
Вводим замену:
Пусть
, тогда
. При такой замене очевидно, что у
принимает строго положительные значения. Получаем:
Решать подобные квадратные уравнения мы умеем, выпишем ответ:
Чтобы удостовериться в правильности нахождения корней, можно выполнить
проверку по теореме Виета, т. е. найти сумму корней и их произведение и сверить
с соответствующими коэффициентами уравнения.
Получаем:
3. Методика решения однородных показательных уравнений второй степени
Изучим следующий важный тип показательных уравнений:
Уравнения такого типа называют однородными второй степени относительно
функций f и g. В левой его части стоит квадратный трехчлен относительно f с
параметром g или квадратный трехчлен относительно g с параметром f.
Методика решения:
Данное уравнение можно решать как квадратное, но легче поступить по-другому.
Следует рассмотреть два случая:
1.
2.
В первом случае получаем
Во втором случае имеем право разделить на старшую степень
Следует ввести замену переменных
относительно у:
и получаем:
, получим квадратное уравнение
Обратим внимание, что функции f и g могут быть любыми, но нас интересует тот
случай, когда это показательные функции.
4. Примеры решения однородных уравнений
Пример 4:
Перенесем все слагаемые в левую часть уравнения:
Воспользуемся свойствами степени и приведем все степени к простым основаниям:
Несложно заметить функции f и g:
Поскольку показательные функции приобретают строго положительные значения,
имеем право сразу делить уравнение на
когда
Получаем:
:
, не рассматривая случай,
Вводим замену:
функции)
Получили квадратное уравнение:
(согласно свойствам показательной
Определяем корни по теореме Виета:
Первый корень не удовлетворяет промежутку значений у, отбрасываем его,
получаем:
Пример 5:
Воспользуемся свойствами степени и приведем все степени к простым основаниям:
Несложно заметить функции f и g:
Поскольку показательные функции приобретают строго положительные значения,
имеем право сразу делить уравнение на
когда
, не рассматривая случай,
:
Получаем:
Вводим замену:
функции)
Получили квадратное уравнение:
(согласно свойствам показательной
Определяем корни:
Первый корень не удовлетворяет промежутку значений у, отбрасываем его,
получаем:
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1.
Mathematics-repetition.com (Источник).
2.
Terver.ru (Источник).
3.
Yourtutor.info (Источник).
Домашнее задание 1.
2. Выучить конспект
Решить уравнение: