Глава 4. Практические приложения
реклама
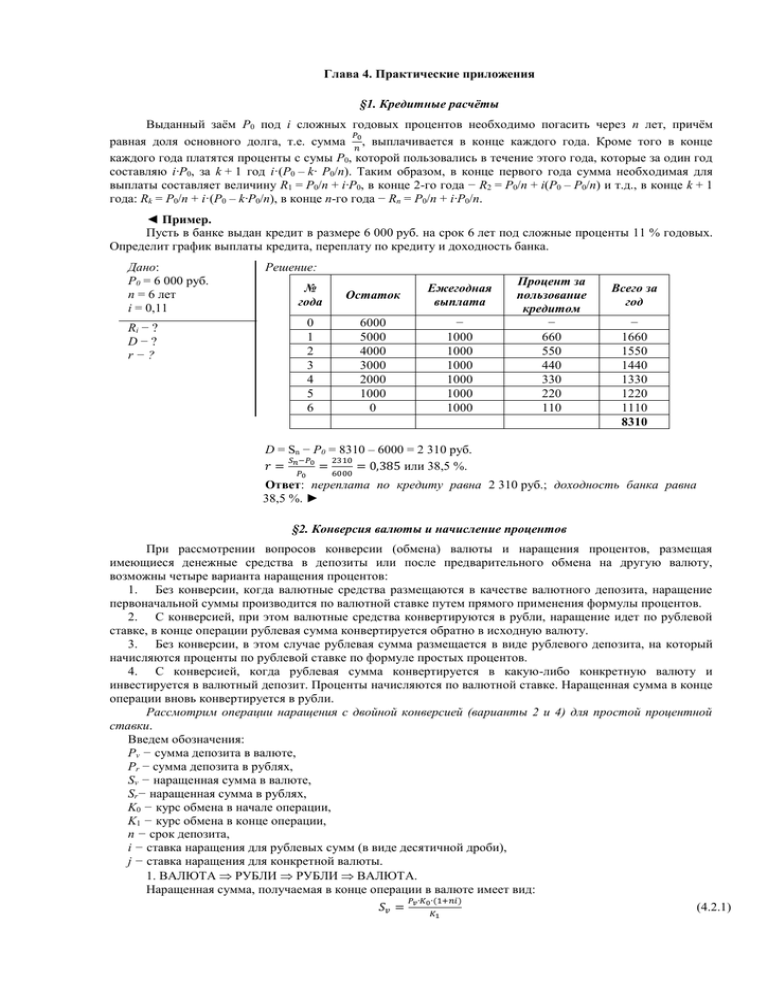
Глава 4. Практические приложения §1. Кредитные расчёты Выданный заём P0 под i сложных годовых процентов необходимо погасить через n лет, причём 𝑃 равная доля основного долга, т.е. сумма 0, выплачивается в конце каждого года. Кроме того в конце 𝑛 каждого года платятся проценты с сумы P0, которой пользовались в течение этого года, которые за один год составляю i·P0, за k + 1 год i·(P0 – k· P0/n). Таким образом, в конце первого года сумма необходимая для выплаты составляет величину R1 = P0/n + i·P0, в конце 2-го года − R2 = P0/n + i(P0 – P0/n) и т.д., в конце k + 1 года: Rk = P0/n + i·(P0 – k·P0/n), в конце n-го года − Rn = P0/n + i·P0/n. ◄ Пример. Пусть в банке выдан кредит в размере 6 000 руб. на срок 6 лет под сложные проценты 11 % годовых. Определит график выплаты кредита, переплату по кредиту и доходность банка. Дано: P0 = 6 000 руб. n = 6 лет i = 0,11 Решение: № года Остаток Ежегодная выплата 0 1 2 3 4 5 6 6000 5000 4000 3000 2000 1000 0 − 1000 1000 1000 1000 1000 1000 Ri − ? D−? r−? Процент за пользование кредитом − 660 550 440 330 220 110 Всего за год − 1660 1550 1440 1330 1220 1110 8310 D = Sn − P0 = 8310 – 6000 = 2 310 руб. 𝑆 −𝑃 2310 𝑟= 𝑛 0= = 0,385 или 38,5 %. 𝑃0 6000 Ответ: переплата по кредиту равна 2 310 руб.; доходность банка равна 38,5 %. ► §2. Конверсия валюты и начисление процентов При рассмотрении вопросов конверсии (обмена) валюты и наращения процентов, размещая имеющиеся денежные средства в депозиты или после предварительного обмена на другую валюту, возможны четыре варианта наращения процентов: 1. Без конверсии, когда валютные средства размещаются в качестве валютного депозита, наращение первоначальной суммы производится по валютной ставке путем прямого применения формулы процентов. 2. С конверсией, при этом валютные средства конвертируются в рубли, наращение идет по рублевой ставке, в конце операции рублевая сумма конвертируется обратно в исходную валюту. 3. Без конверсии, в этом случае рублевая сумма размещается в виде рублевого депозита, на который начисляются проценты по рублевой ставке по формуле простых процентов. 4. С конверсией, когда рублевая сумма конвертируется в какую-либо конкретную валюту и инвестируется в валютный депозит. Проценты начисляются по валютной ставке. Наращенная сумма в конце операции вновь конвертируется в рубли. Рассмотрим операции наращения с двойной конверсией (варианты 2 и 4) для простой процентной ставки. Введем обозначения: Рv − сумма депозита в валюте, Рr − сумма депозита в рублях, Sv − наращенная сумма в валюте, Sr− наращенная сумма в рублях, K0 − курс обмена в начале операции, K1 − курс обмена в конце операции, п − срок депозита, i − ставка наращения для рублевых сумм (в виде десятичной дроби), j − ставка наращения для конкретной валюты. 1. ВАЛЮТА РУБЛИ РУБЛИ ВАЛЮТА. Наращенная сумма, получаемая в конце операции в валюте имеет вид: 𝑃 ∙𝐾 ∙(1+𝑛𝑖) 𝑆𝑣 = 𝑣 0 (4.2.1) 𝐾1 Множитель наращения с учетом двойного конвертирования имеет вид: 𝐾 1+𝑛𝑖 1+𝑛𝑖 𝑚 = 0 ∙ (1 + 𝑛𝑖) = ⁄ = где 𝑘 = 𝐾1 𝐾0 𝐾1 𝐾1 𝐾0 (4.2.2) 𝑘 темп роста обменного курса за срок операции. Доходность операции определяется по формуле: 𝑆 −𝑃 𝑖= 𝑣 𝑣 (4.2.3) 𝑃𝑣 ∙𝑛 Если подставить в формулу (4.2.3) выражение для Sv, (4.2.1), то получим эффективную ставку: 𝑖э = 𝐾 𝑃𝑣 ∙ 0 ∙ (1+𝑛𝑖)−𝑃𝑣 𝐾1 𝑃𝑣 ∙𝑛 = 𝐾0 ∙ (1+𝑛𝑖)−1 𝐾1 𝑛 1 1+𝑛𝑖 𝑘 𝑛 = ∙ − 1 𝑛 (4.2.3) Из (4.2.3) можно сделать вывод, что с увеличением k доходность или эффективная ставка iэ падает, при k = 1 доходность данной операции равна рублёвой ставке процентов, т.е. iэ = i. Если k > 1, то доходность операции меньше рублёвой ставки iэ < i, если k < 1, то больше − iэ > i. При некотором критическом значении k*, доходность операции равна 0 (iэ = 0). В этом случае k* = 1 + ni, (4.2.4) или 𝐾1∗ = 𝐾0 ∙ (1 + 𝑛𝑖) (4.2.5) ∗ Т.е. если величины k или 𝐾1 превышают критические значения, то операция убыточна. Максимально допустимое значение курса обмена в конце операции К1 при котором эффективность будет равна существующей ставке по депозитам в валюте имеет вид: 𝐾 1+𝑛𝑖 max 𝑘 = 1 = (4.2.6) 𝐾0 или 1+𝑛𝑗 max 𝐾1 = 𝐾0 ∙ 1+𝑛𝑖 1+𝑛𝑗 , (4.2.7) где i и j – множители наращения двух альтернативных операций. Таким образом, если обменный курс в конце операции ожидается меньше max K1, то депозит валюты через конверсию в рубли выгоднее валютного депозита 2. РУБЛИ ВАЛЮТА ВАЛЮТА РУБЛИ. Множитель наращения в данном случае находится по формуле: 𝑃 ∙𝐾 ∙(1+𝑛𝑗) 𝑆𝑟 = 𝑟 1 (4.2.8) 𝐾0 Доходность операции определяется по формуле: 𝑖э = 𝑆𝑟 −𝑃𝑟 𝑃𝑟∙𝑛 = 𝐾 𝑃𝑟 ∙ 1 ∙ (1+𝑛𝑗)−𝑃𝑟 𝐾0 𝑃𝑟∙𝑛 = 𝐾1 ∙ (1+𝑛𝑗)−1 𝐾0 𝑛 = 𝑘 ∙ (1+𝑛𝑗)−1 𝑛 (4.2.9) Зависимость показателя эффективности iэ от k линейная, iэ = j при k = 1, it > j при k > 1, iэ < j при k < 1. Критические значения k*, при которых iэ = 0 имеют вид: 1 𝐾 𝑘∗ = или 𝐾1∗ = 0 . (4.2.10) 1+𝑛𝑗 1+𝑛𝑗 Если ожидаемые величины k или К1 меньше своих критических значений, то операция убыточна. Минимально допустимая величина k (темпа роста валютного курса за весь срок операции), обеспечивающая такую же доходность, что и прямой вклад в рублях, имеет вид: 1+𝑛𝑖 min 𝑘 = (4.2.6) 1+𝑛𝑗 или min 𝐾1 = 𝐾0 ∙ 1+𝑛𝑖 1+𝑛𝑗 , (4.2.7) Таким образом, если обменный курс в конце операции ожидается больше min K1, то депозит рублевых сумм через конвертацию в валюту выгоднее рублевого депозита. Рассмотрим операции наращения с двойной конверсией (вариант 2) для сложной процентной ставки. ВАЛЮТА РУБЛИ РУБЛИ ВАЛЮТА. Формула наращённой суммы для сложных процентов имеет вид: 𝑆𝑣 = 𝑃𝑣 ∙𝐾0 ∙(1+𝑖)𝑛 где i − ставка сложных процентов. Множитель наращения находится по формуле: 𝑚= 𝐾0 𝐾1 (4.2.8) 𝐾1 (1 + 𝑖)𝑛 = (1+𝑖)𝑛 𝐾1 ⁄𝐾0 = (1+𝑖)𝑛 𝑘 (4.2.9) 𝑛 𝑆 Т.к. из формулы сложных процентов 𝑖э = √ 𝑣 − 1, то эффективная процентная ставка имеет вид: 𝑃 𝑣 𝑛 𝑃 (1+𝑖)𝑛 ∙ 𝐾0 𝑣 𝐾1 𝑖э = √ 𝑃𝑣 −1= 1+𝑖 𝑛 √𝑘 − 1, (4.2.10) т.е. с увеличением темпа роста k эффективность iэ падает, причём при k = 1 iэ = i, при k > 1 iэ < i, а при k < 1 iэ > i. Если эффективность операции равна нулю, критическое значение k определяется следующим образом: k* = (1 + i)n, (4.2.11) т.е. среднегодовой темп роста курса валюты равен годовому темпу наращения по рублевой ставке. Операция с двойной конверсией считается убыточной (iэ < 0), если ожидаемые величины k или К1 больше своих критических значений. Максимально допустимое значение k, при котором доходность операции будет равна доходности при прямом инвестировании валютных средств по ставке j, находится по формуле: 𝑘𝑚𝑎𝑥 = (1+𝑖)𝑛 (1+𝑗)𝑛 или max 𝐾1 = 𝐾0 (1+𝑖)𝑛 (1+𝑗)𝑛 (4.2.12) Таким образом, если обменный курс в конце операции ожидается меньше max K1, то депозит валюты через конвертацию в рубли выгоднее валютного депозита.

