Геометрические приложения производной. 1. Цель работы: 2. Оборудование:

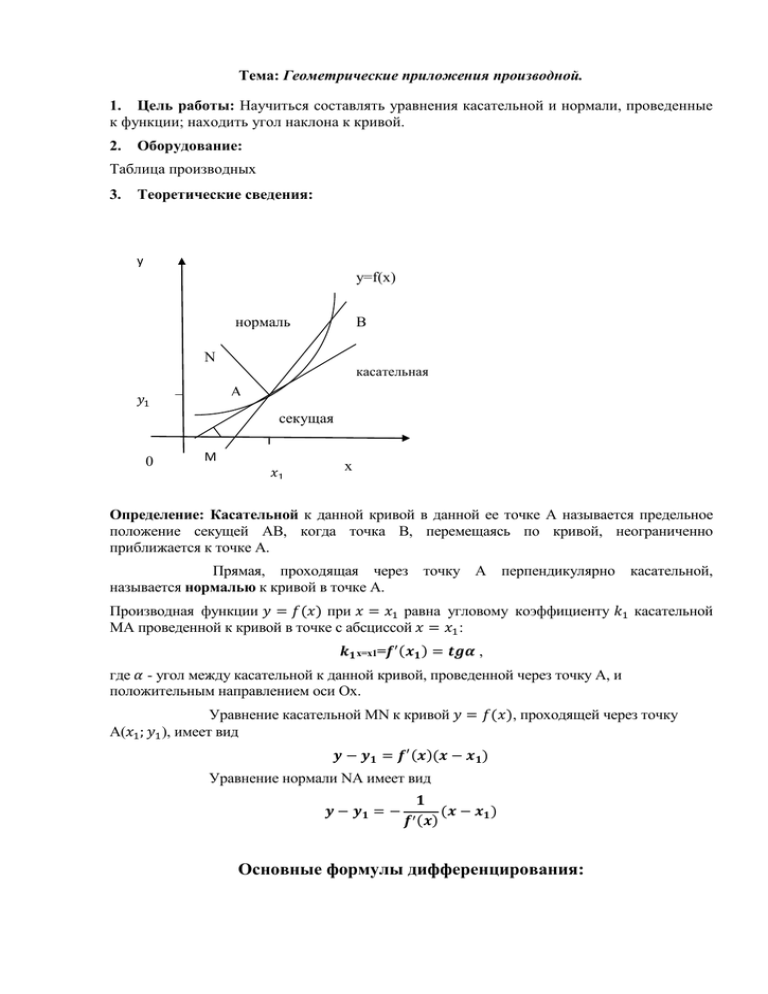
Тема: Геометрические приложения производной.
1. Цель работы: Научиться составлять уравнения касательной и нормали, проведенные
к функции; находить угол наклона к кривой.
2.
Оборудование:
Таблица производных
3.
Теоретические сведения:
y
y=f(x)
нормаль
B
N
касательная
A
𝑦1
секущая
0
M
𝑥1
x
Определение: Касательной к данной кривой в данной ее точке А называется предельное
положение секущей АВ, когда точка В, перемещаясь по кривой, неограниченно
приближается к точке А.
Прямая, проходящая через точку А перпендикулярно касательной,
называется нормалью к кривой в точке А.
Производная функции 𝑦 = 𝑓(𝑥) при 𝑥 = 𝑥1 равна угловому коэффициенту 𝑘1 касательной
MA проведенной к кривой в точке с абсциссой 𝑥 = 𝑥1 :
𝒌𝟏 x=x1=𝒇′ (𝒙𝟏 ) = 𝒕𝒈𝜶 ,
где 𝛼 - угол между касательной к данной кривой, проведенной через точку А, и
положительным направлением оси Ох.
Уравнение касательной MN к кривой 𝑦 = 𝑓(𝑥), проходящей через точку
А(𝑥1 ; 𝑦1 ), имеет вид
𝒚 − 𝒚𝟏 = 𝒇′ (𝒙)(𝒙 − 𝒙𝟏 )
Уравнение нормали NA имеет вид
𝒚 − 𝒚𝟏 = −
𝟏
𝒇′ (𝒙)
(𝒙 − 𝒙𝟏 )
Основные формулы дифференцирования:
1. 𝐶 ′ = 0 (С- постоянная)
2. 𝑥 ′ = 1
3. (𝑢 + 𝑣 − 𝑤)′ = 𝑢′ + 𝑣 ′ − 𝑤 ′ (u,
v,w- функции от x)
4. (𝐶𝑢)′ = 𝐶𝑢′
5. (𝑢𝑣)′ = 𝑢′ 𝑣 + 𝑢𝑣 ′
𝑢
6. (𝑣 )′ =
7.
𝑣𝑢′ −𝑢𝑣 ′
𝑣2
𝑢 ′
𝑢′
(𝐶 ) = 𝐶
𝐶
𝐶𝑣 ′
( 𝑣 )′ = − 𝑣 2
𝑛 ′
𝑛−1
1
1
21. (𝑎𝑟𝑐𝑠𝑖𝑛𝑥)′ = √1−𝑥 2
1
22. (𝑎𝑟𝑐𝑐𝑜𝑠𝑥)′ = − √1−𝑥 2
1
23. (𝑎𝑟𝑐𝑡𝑔𝑥)′ = 1+𝑥 2
1
√𝑥
1
𝑛
( √𝑥 )′ =
12.
1
16. (log 𝑎 𝑥)′ = 𝑥𝑙𝑛𝑎
17. (𝑠𝑖𝑛𝑥)′ = 𝑐𝑜𝑠𝑥
18. (𝑐𝑜𝑠𝑥)′ = −𝑠𝑖𝑛𝑥
1
19. (𝑡𝑔𝑥)′ = cos2 𝑥
20. (𝑐𝑡𝑔𝑥)′ = − sin2 𝑥
8.
9. (𝑥 ) = 𝑛𝑥
1
1
10. (𝑥)′ = − 𝑥 2
11. (√𝑥)′ = 2
13. (𝑒 𝑥 )′ = 𝑒 𝑥
14. (𝑎 𝑥 )′ = 𝑎 𝑥 𝑙𝑛𝑎
1
15. (𝑙𝑛𝑥)′ = 𝑥
𝑛
1
24. (𝑎𝑟𝑐𝑐𝑡𝑔𝑥)′ = − 1+𝑥 2
𝑛 √𝑥 𝑛−1
4. Задания:
Вариант № 1
1. Составить уравнение касательной к параболе 𝑦 = 𝑥 2 − 6𝑥 + 5 в точке с
абсциссой x=4.
2. Составить уравнение касательной и нормали к кривой 𝑦 = 𝑥 2 − 7𝑥 + 10 в
точке x=4.
3. Вычислить острый угол , под которым парабола 𝑦 = 𝑥 2 − 4 пересекает ось
абсцисс.
4. Найти точки графика функции 𝑦 = 𝑥 3 − 3𝑥 2 + 3𝑥 , в которых касательная
параллельна оси абсцисс.
3
5. Составить уравнение касательной к графику функции 𝑦 = 𝑥 в точке с
абсциссой x=-1.
Вариант № 2
1. Составить уравнение касательной к параболе 𝑦 = 2𝑥 2 − 5𝑥 − 3 в точке
с абсциссой x=2.
2. Составить уравнение касательной и нормали к кривой 𝑦 = 2𝑥 3 в точке
x=-1.
3. Вычислить острый угол, под которым парабола 𝑦 = 𝑥 2 − 9 пересекает
ось абсцисс.
1
4. Найти точки графика функции 𝑦 = 2 𝑥 4 + 16𝑥, в которых касательная
параллельна оси абсцисс.
5. Составить уравнение касательной к графику функции 𝑦 = 3 sin 𝑥 в
𝜋
точке с абсциссой x= 2 .
Вариант №3
1. Составить уравнение касательной к параболе 𝑦 = 𝑥 2 + 6𝑥 + 8
в точке с абсциссой x=-2.
2. Составить уравнение касательной и нормали к кривой
𝑦 = 3𝑥 2 − 𝑥 в точке x=-1.
3. Вычислить острый угол, под которым парабола
𝑦 = 𝑥 2 − 𝑥 − 12 пересекает ось абсцисс.
4. Найти точки графика функции 𝑦 = 3𝑥 4 − 6𝑥 2 + 2 , в которых
касательная параллельна оси абсцисс.
5. Составить уравнение касательной к графику функции 𝑦 = 𝑡𝑔𝑥 в
𝜋
точке с абсциссой 𝑥 = 4 .
5.
Содержание отчета
Отчет должен содержать:
1.
2.
3.
4.
6.
Название работы.
Цель работы.
Задания с решениями.
Вывод по работе.
Контрольные вопросы
1. Какое число называют пределом функции f(x)?
2. Сформулировать теоремы о пределах функции.
3. Выписать два замечательных предела.
7. Литература
1. Авдашева С.Б., Розанова Н.М. Теория организации отраслевых рынков. Учебник.-М.:
ИЧП «Издательство Магистр», 1999. – 390 с., илл.