МИНОБРНАУКИ РОССИИ Энгельсский технологический институт (филиал)

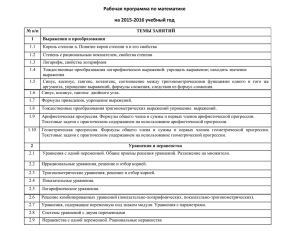
МИНОБРНАУКИ РОССИИ
Энгельсский технологический институт
(филиал)
ФГБОУ ВПО «Саратовский государственный технический университет
имени Гагарина Ю.А.»
Центр непрерывного образования
Утверждаю
Первый заместитель директора
________ И.Г. Остроумов
«____»_____________2011
РАБОЧАЯ ПРОГРАММА
подготовительных курсов по предмету «Математика»
Энгельс-2011
1.
Цели и задачи курса
Программа составлена для курса дополнительных занятий по математике с целью подготовки к сдаче Единого государственного экзамена .
Задачами курса являются:
- выработка и закрепление знаний и умений, которые необходимы для выполнения заданий ЕГЭ по математике;
- обеспечение уровня подготовки выпускников по математике в соответствии с
Обязательным минимумом содержания основных образовательных программ и Требованиями к уровню подготовки выпускников средней (полной) школы (Приказ МО РФ
«Об утверждении федерального компонента Государственных стандартов начального
общего, основного общего и среднего (полного) общего образования от 05.03.2004
№1089).
2.
Требования к знаниям и умениям учащихся
Требования к знаниям и умениям учащихся представлены в табл.1. Требования
определены в соответствии с Кодификатором требований к уровню подготовки выпускников по математике для составления КИМ ЕГЭ 2012г. (разработан Федеральным
институтом педагогических измерений)
Таблица 1.
Код контролируемоКод
го требования (умеСодержание требования (умения)
раздела
ния)
1.
Уметь выполнять вычисления и преобразования
1.1
Выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня
натуральной степени, степени с рациональным показателем, логарифма
1.2
Вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования
1.3
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих
степени, радикалы, логарифмы и тригонометрические функции
2.
Уметь решать уравнения и неравенства
2.1
Решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы
2.2
Решать уравнения, простейшие системы уравнений,
используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод
2.3
Решать рациональные, показательные и логарифмические неравенства, их системы
3.
Уметь выполнять действия с функциями
3.1
Определять значение функции по значению аргумента при различных способах задания функции; описы-
2
3.2
3.3
4.
4.1
4.2
4.3
5.
5.1
5.2
5.3
6.
6.1
6.2
6.3
вать по графику поведение и свойства функций,
находить по графику функции наибольшие и
наименьшие значения; строить графики изученных
функций
Вычислять производные и первообразные элементарных функций
Исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие
значения функций
Уметь выполнять действия с геометрическими
фигурами, координатами и векторами
Решать планиметрические задачи на нахождение
геометрических величин (длин, углов, площадей)
Решать простейшие стереометрические задачи на
нахождение геометрических величин (длин, углов,
площадей, объемов); использовать при решении стереометрических задач планиметрические факты и
методы
Определять координаты точки; проводить операции
над векторами, вычислять длину и координаты вектора, угол между векторами
Уметь строить и исследовать простейшие математические модели
Моделировать реальные ситуации на языке алгебры,
составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры
Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата
алгебры; решать практические задачи, связанные с
нахождением геометрических величин
Проводить доказательные рассуждения при решении
задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения
Уметь использовать приобретенные знания и
умения в практической деятельности и повседневной жизни
Анализировать реальные числовые данные; осуществлять практические расчеты по формулам, пользоваться оценкой и прикидкой при практических
расчетах
Описывать с помощью функций различные реальные
зависимости между величинами и интерпретировать
их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках
Решать прикладные задачи, в том числе социальноэкономического и физического характера, на
3
наибольшие и наименьшие значения, на нахождение
скорости и ускорения
4
3. Содержание учебного курса
Всего предусмотрено 86 академических часов учебных занятий. Распределение
часов учебных занятий по темам приведено в табл.2.
Таблица 2.
№
п/п
Тема занятия. Вопросы, отрабатываемые на занятии
1.
Алгебра
1.1 Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Основные тригонометрические тождества
1.2 Логарифм числа. Логарифм произведения, частного, степени
Кол-во
часов
4
4
1.3 Решение задач раздела Алгебра из открытого сегмента Федерального банк
материаловфункции. Уравнения и неравенства
2. экзаменационных
Элементарные
2.1 Квадратичная функция, график квадратного трехчлена. Квадратные
уравнения и неравенства. Рациональные уравнения и неравенства. Метод интервалов
2.2 Показательная функция, ее график. Показательные уравнения и неравенства
2.3 Логарифмическая функция, ее график. Логарифмические уравнения и
неравенства
2.4 Тригонометрические функции, их графики. Тригонометрические уравнения
2.5 Простейшие системы уравнений с двумя неизвестными
2.6 Решение задач раздела Уравнения и неравенства из открытого сегмента
Федерального банк экзаменационных материалов
3.
Начала математического анализа
2
3.1 Понятие о производной функции, геометрический смысл производной.
Уравнение касательной к графику функции. Физический смысл производной, нахождение скорости для процесса, заданного формулой или
графиком
2
3.2 Производные основных элементарных функций. Общие правила дифференцирования
3.3 Исследование функции с помощью производной
4
3.4 Решение задач раздела Начала математического анализа из открытого
сегмента Федерального банк экзаменационных материалов
4.
Геометрия
4.1 Треугольник, параллелограмм, ромб, квадрат, трапеция
4.2 Окружность и круг
4
4.3 Окружность, вписанная в треугольник, и окружность, описанная около
треугольника
4.4 Решение задач планиметрии раздела Геометрия из открытого сегмента
Федерального банка экзаменационных материалов
2
4.5 Призма, ее основания, боковые ребра, высота, боковая поверхность;
прямая призма; правильная призма. Параллелепипед, куб
2
4
6
6
6
4
6
4
4
2
6
5
Пирамида: основание, боковые ребра, высота, боковая поверхность.
Треугольная пирамида. Правильная пирамида. Цилиндр: основание,
высота, боковая поверхность, образующая, развертка
4.7 Конус: основание, высота, боковая поверхность, образующая, развертка. Шар и сфера
4.8 Решение стереометрических задач раздела Геометрия из открытого
сегмента Федерального банк экзаменационных материалов
5.
Элементы теории вероятностей
4.6
2
2
6
5.1
Вероятности событий
2
5.2
Использование вероятностей при решении прикладных задач
2
Всего:
4.
86
Рекомендуемая литература
1. ЕГЭ 2012. Математика. Типовые тестовые задания /Под ред. А.Л.Семенова,
И.В.Ященко – М.: Издательство «Экзамен», 2012. – 95с.
2. Самое полное издание типовых вариантов заданий ЕГЭ 2012: Математика /Под
ред. А.Л.Семенова, И.В.Ященко. – М.: АСТ, Астрель, 2011. – 93 с.
3. ЕГЭ 2012. Математика: типовые экзаменационные варианты – 30 вариантов задания /Под ред. А.Л.Семенова, И.В.Ященко – М.: Национальное образование,
2011. – 192 с.
4. Панферов В.С. Отличник ЕГЭ. Математика. Решение сложных задач
/В.С.Панферов, И.Н.Сергеев; ФИПИ – М.: Интеллект-Центр, 2010. – 80с.
5.
Информационные ресурсы в сети Интернет
http://ege.edu.ru
портал информационной поддержки проекта
«Единый государственный экзамен»
http://fipi.ru
сайт Федерального института педагогических
измерений (ФИПИ)
http://mathege.ru
Открытый банк задач ЕГЭ по математике
http//i-exam.ru
тестирование в сфере образования
http://uztest.ru
подготовка к ЕГЭ по математике
http://techn.sstu.ru
сайт Энгельсского технологического института
(филиала) СГТУ
Рабочую программу составил
доцент каф. «Высшая математика и механика» ЭТИ (филиала) СГТУ
_____________________
А.В.Серебряков
6