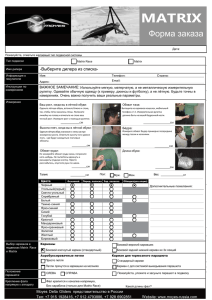
МАТРИЧНЫЕ ВЫЧИСЛЕНИЯ построение и анализ регрессий К матричным объектам в Eviews относятся матрицы (matrix , sym – симметричные матрицы), вектора (vectors), вектора-строки (rowvector) . С правилами задания размерности этих объектов можно ознакомиться в разделе помощи Matrix Language (Help – User Guide I- Matrix Language) , список и описание всех доступных команд - в разделе Matrix Reference (Help – Quick Help Reference – Matrix Reference). Матричный вид МНК Матрицы, вектора можно задавать как вручную, создав новый объект Object-New Object-Matrix-Vector-Coef и вводя затем значение каждого элемента, либо преобразовывать в столбцы, вектора переменные или группы переменных. Создайте матрицу размерностью 3*3 с названием mx1 , содержащую следующие элементы (Help - User Guide I – Matrix Language - Assigning Matrix Values): 1 2 3 Mx1 = 4 8 7 9 6 5 Используйте возможность создания нового объекта или воспользуйтесь командами. (matrix (3,3) mx1 Mx1.fill 1,4,9,2,8,6,3,7,5 ) Поэкспериментируйте с созданием и изменением матричных объектов. Попробуйте например извлечь из этой матрицы (функция @extract) вторую строку (rowvector str2=@extract…). А затем выполните присваивание mx1=str2. Что произойдет? Вспомните как происходит умножение матричных объектов, проверьте на простых примерах. Вспомните как обращаются матрицы 2Х2 Загрузите файл base3.xls (*wf1) Попробуем оценить коэффициенты регрессии: rent = β0+ β 1*dist+ β 2*rm+ β 3*no+ Создайте матрицу регрессоров x из группы переменных rm, dist и no. Не забудьте добавить первым столбцом константу (используйте команды stom, stomna: Help – Quick Help Reference – Matrix Reference). series const=1 Group grp1 const rm dist no 1 stomna(grp1, x) или matrix x x=grp1 Создайте вектор y из объясняемой переменной rent. stomna(rent,y) Вспомним формулу вычисления коэффициентов регрессии в матричном виде: ( X ' X ) 1 X ' Y Создайте матрицу x_tr – транспонированную матрицу x, перемножьте ее с исходной. Попробуйте создать обратную матрицу (X'X)-1. Matrix x_tr=@transpose(x) Matrix x_x = x_tr*x !!! Проверьте перед обращением матрицы, что она хорошо обусловлена- ее определитель (determinant) и макимальное собственное число (eigenvalue) - достаточно отличны от нуля. Сохраните значение опрелителя в какой-нибудь константе, а значения собственных чисел - в каком-нибудь векторе. !! Найдите квадратный корень из этой матрицы. Matrix x_inv = @inverse(x_x) Matrix x_y=x_tr*y Coef betas = x_inv*x_y Проверьте правильность вычисления коэффициентов, построив регрессию – откройте соответствующие выделенные переменные, как уравнение (Open – As Equation) или создайте его как новый объект, или используйте меню Proc в группе. Создайте переменную y_hat, содержащую предсказанные значения переменной rent. (сгенерируйте новую переменную вручную: воспользуйтесь матричной формулой y x , а затем переведите полученный вектор в серию с помощью команды mtos, либо воспользуйтесь кнопкой Forecast в объекте Equation.) Создайте переменную (вектор) остатков, исследуйте их: посмотрите дескриптивные стаистики, проверьте на нормальность, убедитесь, что они ортогональны регрессорам. Увеличьте размер файла на пару наблюдений, и заполните на свой выбор значения регрессоров. Спрогнозируйте значения зависимой переменной. 2 Вычислите: ^ n n сумму квадратов остатков Rss i 1 ( yi y i ) 2 i 1 ei e ' e дисперсию остатков RMS = RSS/(n-k) стандартную ошибку регрессии RMSE= RMS коэффициент детерминации _ ^ ^ n n 2 2 ( y y ) ( y Ess Rss i i yi ) i R2 i 1 i 1 1 1 _ _ n n Tss Tss 2 2 ( y y ) ( y y ) i1 i i1 i матрицу ковариации коэффициентов ^ V ( OLS ) 2 ( X ' X ) 1 RMS ( X ' X ) 1 ^ ^ ^ var( 1 ) cov( 1 , 2 ) ... ^ ^ ^ var( 2 ) .. cov( 2 , 1 ) ... ... ... ... ... ... ^ ^ cov( , ) ... .... k 1 ^ ^ ... cov( 1 , k ) ^ ^ ... cov( 2 , k ) ... ... ... ... ^ ... var( k ) ^ ^ стандартные ошибки коэффициентов St.Error ( i ) var( i ) Сравните с вычислениям Eviews, содержащимися в Equation-View-Estimation Output =). stomna(y_hat, yh) scalar rss= @transpose(yh-y)*(yh-y) scalar rms=rss/(32-3) scalar rmse = rms^0.5 matrix covar_coef = x_inv*rms matrix var_coef=@getmaindiagonal(covar_coef) scalar st_err_const = var_coef(1)^0.5 scalar st_err_rm= var_coef(2)^0.5 scalar st_err_dist = var_coef(3)^0.5 scalar st_err_no= var_coef(4)^0.5 scalar r_sq = 1-rss/(@var(rent)*@obs(rent)) Проинтерпретируйте модель, ожидаемы ли знаки коэффициентов? Что можно сказать о качестве подгонки? Посчитайте коэффициенты корреляции между регрессорами, вычислите определитель матрицы X'X (вам могут пригодиться функции cor, @cor, @det). Какие выводы можно сделать? Как можно улучшить модель? Постройте модель в новой спецификации =)). 3 Свойства МНК-оценок коэффициентов регрессии Откройте программу for_coef.prg и запустите ее (File-Open-Programm-Run). Эта программа позволяет с помощью метода Монте-Карло изучить статистические свойства МНК-оценок. С помощью нее создается выбираемое количество парных регрессий из теоретической регрессии с известными параметрами добавлением случайной составляющей. y * x ^ ^ y i i * xi i Программа имеет 4 параметра, которые необходимо указать в диалоговом окне в поле «Program arguments» (либо перечислить сразу после команды в командной строке – run for_coef %0 %1 %2 %3) , где : %0 – количество наблюдений в выборках %1 – количество создаваемых парных регрессий %2 – коэффициент при собственном регрессоре %3 – коэффициент при константе Коэффициенты каждой из регрессии будут сохраняться в переменные alphas и betas соответственно =) Укажите параметры на ваше усмотрение. Посмотрите на распределение оценок коэффициентов – проанализируйте описательные статистики, постройте графики распределения, плотности. Каким должно быть распределение оценок? Проведите несколько таких экспериментов (результаты будут сохраняться каждый раз на новой странице рабочего файла), меняя количество построенных регрессий, количество наблюдений. Посмотрите, как будет меняться их распределение. Сделайте выводы =) 4