Сопротивление материалов. Вариант 5. Ответы

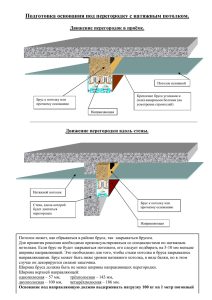
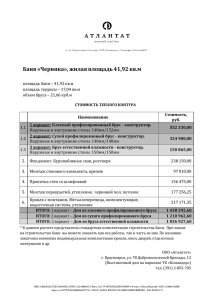
Вариант 5
Вопрос 1
Выбрать соответствующую эпюру продольных сил в поперечных
сечениях бруса.
Составим расчетную схему задачи.
Разобьем брус на участки.
Построим эпюру продольных сил
по границам сечений используя
метод сечений.
N I  0;
N II  N I  70  70 кН;
N III  N II  70 кН;
N IV  N III  30  70  30  40 кН.
Ответ: Код ответа «3»
верно изображена эпюра под буквой «В»;
Вопрос 2
Для бруса из вопроса 1 определить наибольшую продольную силу,
возникшую в поперечном сечении.
Ответ: код ответа «3»
наибольшая продольная сила равна 70 кН.
Вопрос 3
Определить нормальное напряжение в сечении С–С бруса из вопроса 1
Нормальное напряжение в сечении определяется как отношение
нормальной (продольной) силы, действующей в сечении к площади этого
сечения.
Имеем
NIII N III
70 103
CC  III 


 280  106 Па=280 МПа.
6
AIII A 2 250 10
Ответ: код ответа «3»
нормальное напряжение в сечении С–С равно 280 МПа.
Вопрос 4
Обеспечена ли прочность бруса в сечении С–С (вопрос 3), если
известны механические характеристики материала:
σт=540
МПа;
σВ=800
МПа:
допускаемый
коэффициент
запаса
прочности 1,5.
Схема бруса представлена на рисунке к вопросу 1.
Для пластичного материла (сталь) пределом прочности считается предел
текучести, после которого материал получает деформацию без увеличения
нагрузки.
Для хрупкого материала (чугун) пределом прочности считается σВ,
после которого наступает разрушение материала.
Предполагая, что брус изготовлен из пластичного материала, имеем
CC  III  280 МПа<[] 
Т 540
=
=360 МПа.
n 1.5
Предполагая, что брус изготовлен из хрупкого материала, имеем
CC  III  280 МПа<[] 
B 800
=
 533.33 МПа.
n 1.5
В любом случае прочность бруса обеспечена
Ответ: код ответа «1»
<[].
Вопрос 5
Однородная жесткая плита весом G = 10 кН нагружена силой F = 8 кН.
Длина стержня АВ = 3 м; материал — сталь Е = 2105 МПа;
форма поперечного сечения — двутавр № 10.
Определить удлинение стержня АВ.
Чтобы определить значение растягивающей силы (обозначим ее как
NAB), возникающей в стержне АВ, составим уравнение статического
равновесия плиты относительно левой опоры.
M левая опора  0;
F  sin 45  3  G  5  NAB  10  0.
Откуда определим искомую силу
N AB 
F  sin 45  3  G  5 8  sin 45  3  10  5

 6.70 кН.
10
10
Зная усилие в стержне и площадь сечения стержня (Адв=12 см2 для
двутавра №10 ГОСТ 8239–89), определим удлинение стержня
N AB  lAB
6.70  103  3
lAB =
=
 0.084  103 м=0.084 мм.
11
4
E  A дв
2 10 12 10
Ответ: код ответа «2». lAB = 0.084 мм – удлинение стержня АВ.