1.6. Классификация простых нагружений по внутренним

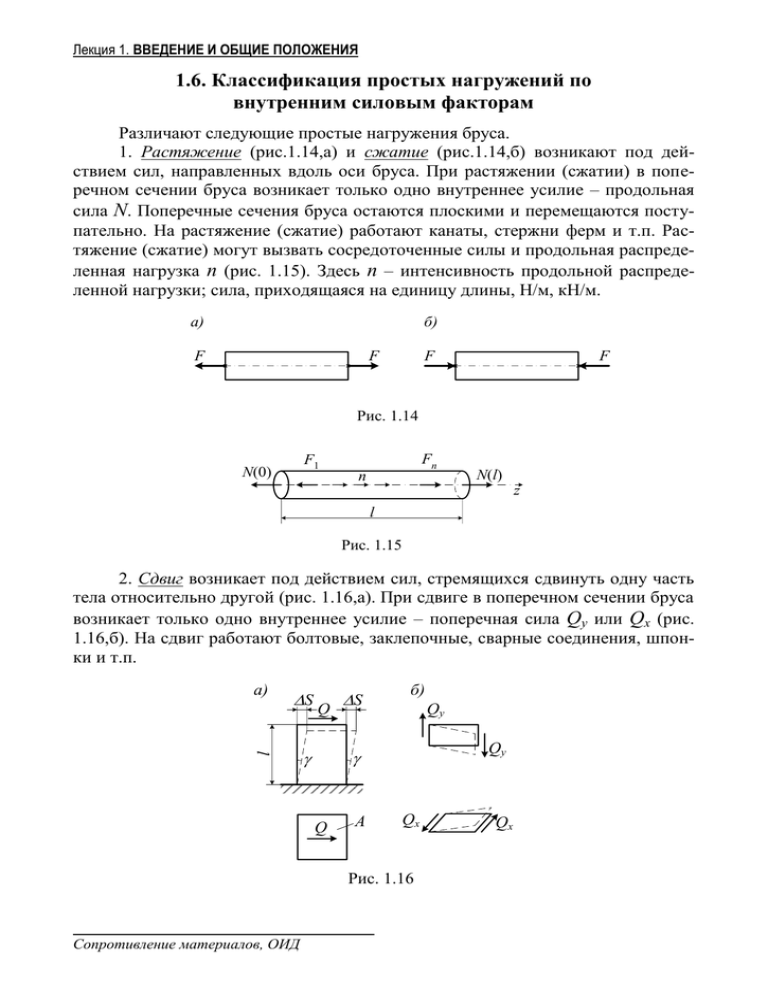
Лекция 1. ВВЕДЕНИЕ И ОБЩИЕ ПОЛОЖЕНИЯ
1.6. Классификация простых нагружений по
внутренним силовым факторам
Различают следующие простые нагружения бруса.
1. Растяжение (рис.1.14,а) и сжатие (рис.1.14,б) возникают под действием сил, направленных вдоль оси бруса. При растяжении (сжатии) в поперечном сечении бруса возникает только одно внутреннее усилие – продольная
сила N. Поперечные сечения бруса остаются плоскими и перемещаются поступательно. На растяжение (сжатие) работают канаты, стержни ферм и т.п. Растяжение (сжатие) могут вызвать сосредоточенные силы и продольная распределенная нагрузка n (рис. 1.15). Здесь n – интенсивность продольной распределенной нагрузки; сила, приходящаяся на единицу длины, Н/м, кН/м.
а)
б)
F
F
F
F
Рис. 1.14
F1
N(0)
Fn
n
N(l)
z
l
Рис. 1.15
2. Сдвиг возникает под действием сил, стремящихся сдвинуть одну часть
тела относительно другой (рис. 1.16,а). При сдвиге в поперечном сечении бруса
возникает только одно внутреннее усилие – поперечная сила Qy или Qx (рис.
1.16,б). На сдвиг работают болтовые, заклепочные, сварные соединения, шпонки и т.п.
S
l
а)
Q
S
б)
Qy
Qy


Q
A
Qx
Рис. 1.16
Сопротивление материалов, ОИД
Qx
Лекция 1. ВВЕДЕНИЕ И ОБЩИЕ ПОЛОЖЕНИЯ
3. Кручение возникает под действием пар сил, лежащих в плоскостях,
перпендикулярных оси бруса, и направленных в противоположные стороны
(рис.1.17). При кручении в поперечном сечении возникает только одно внутреннее усилие – крутящий момент Т. Поперечные сечения остаются плоскими,
поворачиваются относительно друг друга, оставаясь параллельными. На кручение работают валы машин. Кручение могут вызывать сосредоточенные внешние скручивающие пары сил и распределенная моментная крутящая нагрузка t
(рис.1.18). Здесь t – интенсивность моментной крутящей распределенной
нагрузки; пара сил, приходящаяся на единицу длины, Нм/м, кНм/м. Индекс е у
внешних скручивающих моментов от external (англ.) – внешний.
T
T
T(0)
T(l)
t
z
T1e T2e
Рис. 1.17
Tne
Рис. 1.18
4. Изгиб возникает под действием сил, перпендикулярных к оси бруса и
пересекающих эту ось (рис. 1.19). Поперечный изгиб будет плоским, если все
внешние силы и реакции лежат в одной плоскости, проходящей через главную
центральную ось поперечного сечения бруса. При плоском поперечном изгибе
в вертикальной плоскости в поперечном сечении возникают два внутренних
усилия: поперечная сила Qy и изгибающий момент Мх (при изгибе в горизонтальной плоскости – Qх, Мy). При плоском поперечном изгибе поперечные сечения бруса остаются плоскими, поворачиваются относительно друг друга, переставая быть параллельными (рис.1.19). Изгиб могут вызывать сосредоточенные внешние силы, сосредоточенные пары сил, поперечная распределенная
нагрузка qy (или qх), распределенная моментная изгибающая нагрузка mx (или
my), рис. 1.20. Здесь qy (или qх) – интенсивность поперечной распределенной
нагрузки; сила, приходящаяся на единицу длины, Н/м, кН/м; а mx (или my) –
интенсивность моментной изгибающей распределенной нагрузки; пара сил,
приходящаяся на единицу длины, Нм/м, кНм/м.
y F 
1 1
A
F2
y F
1
Qy(0)
n F n
RA
B
mx
Fn
z
RB
Рис. 1.19
qy
Mx(0)
l
M
My(l)
z
Qy(l)
Рис. 1.20
Комбинацию простых нагружений называют сложным сопротивлением.
Сопротивление материалов, ОИД