Вариант 5
Исходные данные
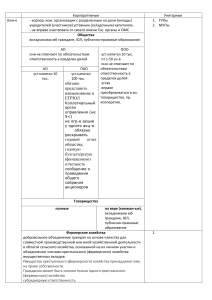
Рисунок 1 – Схема электрической цепи.
E1=80 B; R1=15 Oм; J2=9 A; R2=9 Ом; L=55 мГн; C=30 мкФ;
R4=45 Ом; R5=60; R6=65; φ=-60 град;
1.1 Обоснование выбора метода расчета
В ЭЦ действуют два источника электрической энергии (ИЭЭ):
источник постоянного напряжения E1 и источник переменного тока j2(t).
Поскольку ЭЦ линейная, то возможно применение принципа суперпозиции
(наложения). Сначала выполняется расчет на постоянном токе, при этом
источник переменного тока исключается по правилу: ветвь с j2(t)
размыкается, ветвь с R2 остается. Затем выполняется расчет на переменном
токе, при этом источник постоянного напряжения принимается E1=0 т.е
закорачивается, сопротивление остается. После этого результирующие токи и
напряжения получаются алгебраическим суммированием их составляющих
по постоянному и переменному току.
1.2 Расчет ЭЦ методом эквивалентных преобразований
Рисунок 2 – Преобразования ЭЦ
R46=45+65=110 Ом;
𝑅465 =
110 ∗ 60
= 38,8 Ом
110 + 60
Rэкв=15+9+38,8=62,82 Ом
По закону Ома:
𝐼1 =
𝐸1
80
=
= 1,27 А
𝑅экв 62,8
𝑈 =I1*R456=1,27*38,8=49,3 В
𝐼46 =
𝐼5 =
𝑈
49,3
=
= 0,45 А
𝑅46 110
𝑈
49,3
=
= 0,82 А
𝑅5
60
Напряжение на емкости C:
𝑈𝐶 = 𝐼1 ∗ 𝑅456 = 1,27 ∗ 38,8 = 49,3 В
𝑃𝐸𝐼 = 𝐸1 ∗ 𝐼1 = 1,27 ∗ 80 = 101,6 Вт
𝑃потреб. = 1,272 ∗ 15 + 0,452 ∗ 110 + 0,822 ∗ 60 + 1,272 ∗ 9 = 101,33 Вт
1.3.1 Расчет ЭЦ в комплексной форме методом узловых напряжений
Рисунок 3 - Расчетная ЭЦ на переменном токе
Источник тока в показательной форме комплексной величины
𝑗𝜑
𝑗 = 𝐽 ∗ 𝑒𝑗2 = 9 ∗ 𝑒 𝑗∗(−60°)А
он же в алгебраической форме комплексной величины
𝑗2 = 𝐽2 𝑐𝑜𝑠𝜑𝑗2 + 𝑗 ∗ 𝐽2𝑠𝑖𝑛𝜑𝑗2 = 9 ∗ 0,5 + 𝑗9 ∗ (−0,87) = 4,5 − 𝑗7,79 А
Источник напряжения, преобразованный из источника тока,
𝐸̇2 = 𝑗2 ∗ 𝑅2 = 9 ∗ 9 ∗ 𝑒 −60°𝑗 = 80,97 ∗ 𝑒 −60°𝑗 В
𝐸̇2 = 81 ∗ cos(−60°) + 𝑗81 ∗ sin(−60°) = 40,5 − 𝑗70,11 В
Емкостное сопротивление
𝑍С =
1
1
∗ 𝑒 𝑗𝜑𝐺 −
∗ 𝑒 −𝑗90 = 33,3 ∗ 𝑒 −𝑗90 Ом
−5
𝜔𝐶
1000 ∗ 30 ∗ 10
𝑍С = 300 ∗ cos(−90°) + 𝑗300 ∗ sin(−90°) = −𝑗33,3 Ом
Индуктивное сопротивление
𝑍𝐿 = 𝜔𝐿𝑒 𝑗𝜑𝐿 = 1000 ∗ 0,055 ∗ 𝑒 𝑗90° = 55 ∗ 𝑒 𝑗90° Ом
𝑍𝐿 = 55 ∗ 𝑐𝑜𝑠90° + 𝑗55 ∗ 𝑠𝑖𝑛90° = 𝑗55 Ом
Сопротивления ветвей:
𝑅12 = 𝑅1 + 𝑅2 = 15 + 9 = 24 Ом
𝑅46 = 𝑅4 + 𝑅6 = 45 + 65 = 110 Ом
ЭЦ на рис.4 содержит пять ветвей и три узла. Расчет линейной ЭЦ
переменного тока выполняем методом узловых напряжений, как более
рациональным.
Рисунок 4 - Последовательность преобразований ЭЦ
Последовательность преобразований показана на рисунках выше, где
принято следующее:
𝑍5𝐶 =
𝑅5 𝑍𝐶
𝑅5𝑍𝐶
60 ∙ (−𝑗33,3)
=
=
= 14,13 − 𝑗25,46
𝑅5 + 𝑍𝐶
𝑅5 + 𝑍𝐶
60 − 𝑗33,3
= 29,12𝑒 −𝑗60,97 Ом;
𝑍46𝐿 = 𝑅46 + 𝑍𝐿 = 110 + 𝑗55 = 122,98 ∙ 𝑒 𝑗26,57 Ом;
𝑍46𝐿 ∙ 𝑍5𝐶
122,98 ∙ 𝑒 𝑗26,57 ∙ 29,12𝑒 −𝑗60,97 3581,18𝑒 −𝑗34,4
𝑍456𝐿𝐶 =
=
=
𝑍46𝐿 + 𝑍5𝐶
110 + 𝑗55 + 14,13 − 𝑗25,46
127,6𝑒 𝑗13,39
= 28,07𝑒 −𝑗47,79 Ом;
𝑍456𝐿𝐶 = 18,86 − 𝑗20,79 Ом;
𝑍экв = 𝑍456𝐿𝐶 + 𝑅12 = 18,86 − 𝑗20,79 + 24 = 47,64𝑒 −𝑗25,88 Ом;
Комплексные токи и напряжения (по закону Ома):
Е2
80,97𝑒 −𝑗60
𝐼12 =
=
= 1,7𝑒 −𝑗34,12 А;
−𝑗25,88
𝑍экв 47,64𝑒
𝑈456𝐿𝐶 = 𝐼1 ∙ 𝑍456𝐿𝐶 = 1,7𝑒 −𝑗34,12 ∙ 28,07𝑒 −𝑗47,79 = 47,72𝑒 −𝑗81,91 𝐵;
𝑈456𝐿𝐶 47,72𝑒 −𝑗81,91
𝐼𝐶 =
=
= 1,43𝑒 𝑗8,09 А;
𝑍𝐶
33,3 ∙ 𝑒 −𝑗90
𝑈5𝐶 = 𝑈456𝐿𝐶
𝑈456𝐿𝐶 47,72𝑒 −𝑗81,91
𝐼5 =
=
= 0,8𝑒 −𝑗81,91 А;
𝑅5
60
𝑈456𝐿𝐶
47,72𝑒 −𝑗81,91
𝐼𝐿 =
=
= 0,39𝑒 −𝑗108,48 А;
𝑗26,57
𝑍46𝐿
122,98 ∙ 𝑒
𝑈𝐿 = 𝐼𝐿 𝑍𝐿 = 0,39𝑒 −𝑗108,48 ∙ 55 ∙ 𝑒 𝑗90 = 21,45𝑒 −𝑗18,48 В;
𝑈12 = 𝐼12𝑅12 = 1,7𝑒 −𝑗34,12 ∙ 24 = 40,8𝑒 −𝑗34,12 В;
𝑈46 = 𝐼𝐿 𝑅46 = 0,39𝑒 −𝑗108,48 ∙ 110 = 42,9𝑒 −𝑗108,48 В.
1.3.2 Построение векторных диаграмм токов и напряжений на
комплексной плоскости.
Векторная диаграмма токов дана на рис. 5, откуда следует:
𝐼12 = 𝐼𝐿 + 𝐼𝐶 + 𝐼5 ;
Рисунок 5 - Векторная диаграмма токов
Векторная диаграмма напряжений дана на рис. 6, откуда следует:
Е2 = 𝑈12 + 𝑈5𝐶 ;
𝑈5𝐶 = 𝑈46 + 𝑈𝐿 ;
Проверка по законам Кирхгофа выполняется.
Рисунок 6 - Векторная диаграмма напряжений
Полученные выражения токов и напряжений ветвей в комплексной
форме переводим в функции времени.
Непосредственно перед коммутацией при t=0ˉ
𝑗2 (𝑜 − ) = 𝑗2− = 𝐼2𝑚 ∙ 𝑐𝑜𝑠𝜑𝑗2 = 9√2 ∙ cos(−60) = 6,36 𝐴
Аналогично, находим токи и напряжения ветвей:
𝑈𝐶 (𝑜 − ) = 𝑈𝑐𝑚 ∙ 𝑐𝑜𝑠𝜑𝑢𝑐 = √2 ∙ (47,72) ∙ cos(81,91°) = 9,49 𝐵
𝑖𝐶 (𝑜 − ) = 𝑖𝑐𝑚 ∙ 𝑐𝑜𝑠𝜑𝑖𝑐 = √2 ∙ (1,43) ∙ cos(8,09°) = 2 𝐴
𝑈𝐿 (𝑜 − ) = 𝑈𝐿𝑚 ∙ 𝑐𝑜𝑠𝜑𝑢𝐿 = √2 ∙ (21,45) ∙ cos(18,48°) = 28,77 𝐵
𝑖𝐿 (𝑜 − ) = 𝑖𝐿𝑚 ∙ 𝑐𝑜𝑠𝜑𝑖𝐿 = √2 ∙ (0,39) ∙ cos(108,48°) = −0,17 𝐴
𝑖1 (𝑜 − ) = 𝑖1𝑚 ∙ 𝑐𝑜𝑠𝜑𝑖1 = √2 ∙ (1,7) ∙ cos(34,12°) = 1,99 𝐴
𝑖5 (𝑜 − ) = 𝑖5𝑚 ∙ 𝑐𝑜𝑠𝜑𝑖5 = √2 ∙ (0,8) ∙ cos(81,91°) = 0,16 𝐴
Переходим к расчету результирующих токов и напряжений при t=0ˉ.
1.4 Расчет результирующих токов и напряжений ветвей ЭЦ (t=0ˉ)
Согласно принципу суперпозиции, результирующие токи и напряжения
ветвей линейной ЭЦ равны алгебраической, т.е. с учетом знаков, сумме их
составляющих от постоянного и гармонического ИЭЭ. За положительное
направление принимаем направление токов и напряжений от постоянного
ИЭЭ.
Результирующие токи и напряжения ветвей при t=0ˉ:
𝐼1– = 𝐼1 − 𝐼1(0– ) = 1,27 + 1,99 = 3,26 А ;
𝐼2– = 𝐼2 − 𝐼2(0– ) = 1,27 − 1,99 = −0,72 А ;
𝐼5– = 𝐼5 + 𝐼5(0– ) = 0,82 + 0,16 = 0,98 А;
𝐼𝐿– = 𝐼𝐿 + 𝐼𝐿 (0– ) = 0,45 − 0,17 = 0,28 А;
𝐼𝐶– = 𝐼𝐶 + 𝐼𝐶 (0– ) = 0 + 2 = 2 А;
𝑈𝐶– = 𝑈𝐶 + 𝑈𝐶 (0– ) = 49,3 + 9,49 = 58,79 В;
𝑈𝐿– = 𝑈𝐿 + 𝑈𝐿 (0– ) = 0 + 28,77 = 28,77 В .
Эти величины используем при расчете переходного процесса в
линейной ЭЦ.
2. Исследование переходного процесса в линейной ЭЦ
классическим методом
2.1. Составление уравнений переходного процесса
В рассматриваемом примере 𝑆1 замыкается, образуя два независимых
контура. Подлежит рассмотрению контур с постоянным ИЭЭ.
Целью исследования переходного процесса в ЭЦ на рисунке 7
является расчет и построение зависимостей 𝑢𝐶 (𝑡), 𝑖𝐿 (𝑡). Расчет может быть
выполнен классическим методом с решением системы дифференциальных
уравнений или операционным методом с применением преобразований
Лапласа, а также методом уравнений состояния с использованием
компьютерного моделирования и др.
Рисунок 7 – Схема для исследования переходного процесса в ЭЦ
В классическом методе анализа переходных процессов в линейных ЭЦ с
двумя реактивными элементами С и L искомые зависимости представляются
в виде:
𝑈𝐶 (𝑡) = 𝑈𝐶уст + 𝑈𝐶св (𝑡) = 𝑈𝐶уст + 𝐴1𝑒 𝑎1 𝑡 + 𝐴2𝑒 𝑎2 𝑡 ;
𝑖𝐿 (𝑡) = 𝐼𝐿уст + 𝑖𝐿св (𝑡) = 𝐼𝐿уст + 𝐵1 𝑒 𝑎1 𝑡 + 𝐵2 𝑒 𝑎2 𝑡
Где 𝑈𝐶уст , 𝐼𝐿уст – установившиеся значения напряжения на емкости и
индуктивности;
𝑈𝐶св (𝑡), 𝑖𝐿св (𝑡) – свободные составляющие переходного процесса;
𝐴1 , 𝐴2 , 𝐵1 , 𝐵2
–
постоянные
интегрирования,
𝛼1, 𝛼2
–
корни
характеристического уравнения.
Выполняем расчеты в последовательности:
при t=0+, т.е сразу после коммутации (открытия) ключа 𝑆1 ;
при t → ∞, т.е в установившемся режиме после коммутации;
при 0+ ≤ t < ∞, т.е переходный процесс.
2.2 Определение начальных значений токов и напряжений (t=0+)
Цель расчета: определение значений 𝑈𝐶+ , 𝐼𝐶+ , 𝑈𝐿+ , 𝐼𝐿+ , они необходимы при
нахождении постоянных интегрирования переходного процесса.
По законам коммутации
𝑈𝐶+ = 𝑈𝐶− = 58,79 В,
𝐼𝐿+ = 𝐼𝐿− = 0,28 А.
Расчет ЭЦ по схеме на рисунке 8 выполняем по ЗТК и ЗНК.
Рисунок 8 – Схема для расчета ЭЦ по ЗТК и ЗНК
ЗТК: {−𝐼1+ + 𝐼𝐿+ + 𝐼5+ + 𝐼С+ = 0 (3)
𝐼1+ 𝑅1 + 𝑈𝐶+ = 𝐸1
ЗНК: { −𝑈𝐶+ + 𝐼5+ 𝑅5 = 0
𝑈𝐿+ + 𝐼𝐿+ 𝑅46 − 𝐼5+ 𝑅5 = 0
контура 𝐼 (4)
контура 𝐼𝐼 (5)
контура 𝐼𝐼𝐼 (6)
Решаем системы уравнений:
из (5) 𝐼5+ =
из (4) 𝐼1+ =
𝑈𝐶+
𝑅5
= 0,98 𝐴 (7)
𝐸1 −𝑈𝐶+
𝑅1
= 1,41 𝐴 (8)
Подставим (7) и (8) в (3):
−
𝐸1 −𝑈𝐶+
𝑅1
𝑈𝐶+
+
+ 𝐼𝐿 + + 𝐼С+ =0 (9)
𝑅
5
Из (6) 𝑈𝐿+ = 𝐼5+ 𝑅5 − 𝐼𝐿+ 𝑅46 = 0,98 ∗ 60 − 0,28 ∗ (45 + 65) = 28 В (10)
Из (9) 𝐼С+ =
𝐸1 −𝑈𝐶+
𝑅1
− 𝐼𝐿+ −
𝑈𝐶+
𝑅5
= 0,15 𝐴 (11)
Итого, получаем:
𝑈𝐶+ = 58,79 𝐵; 𝐼𝐿+ = 0,28 𝐴; 𝐼С+ = 0,15 𝐴; 𝑈𝐿+ = 28 𝐵;
(12)
2.3 Определение установившихся значений токов и напряжений
(t→∞)
Цель
работы:
определение
значений
𝑈𝐶уст , 𝐼Суст, 𝑈𝐿уст, 𝐼𝐿уст,
которые
необходимы при нахождении постоянных интегрирования.
Расчетная схема дана на рисунке 9. Расчет выполняем методом
эквивалентных преобразований:
Рисунок 9 - Расчетная схема
𝑅46 = 𝑅4 + 𝑅6 = 110 Ом;
𝑅456 =
𝑅46 𝑅5
= 38,82 Ом;
𝑅46 + 𝑅5
𝑅экв = 𝑅1 + 𝑅456 = 53,82 Ом:
Ток источника 𝐸1 :
𝐼1уст =
𝐸1
80
=
= 1,49 А;
𝑅экв 53,82
Напряжение и токи ветвей:
𝑈𝐶уст = 𝑈1уст = 𝐼1уст𝑅1 = 22,35 В;
𝑈456𝐿уст = 𝐼1уст𝑅456 = 57,84 В;
𝐼𝐿уст =
𝑈456𝐿уст
= 0,53 А;
𝑅46
Итого, получаем:
𝑈𝐿уст = 0 В; 𝐼𝐿уст = 0,53 А; 𝑈Суст = 22,35 В; 𝐼Суст = 0 А.
(13)
2.4 Формирование системы дифференциальных уравнений
Составляем систему алгебраических уравнений по законам Кирхгофа
для узлов 1,2 и контуров К1, К2, К3 схемы на рисунке 10.
Рисунок 10 – Расчетная схема
ЗТК узла: −𝐼1 + 𝐼𝐿 + 𝐼𝑐 + 𝐼5 = 0 (14)
ЗНК контура I: 𝑖1 𝑅1 + 𝑢𝑐 = 𝐸1 (15)
ЗНК контура II: 𝑖5 𝑅5 − 𝑢𝑐 = 0 (16)
ЗНК контура III: 𝑖𝐿 𝑅46 + 𝑢𝐿 − 𝑖5 𝑅5 = 0 (17)
Из (14) 𝐼1 = 𝐼𝐿 + 𝐼𝑐 + 𝐼5 (18)
Подставляем (18) и в (15) (16) (17):
𝑖𝐿 𝑅1 + 𝐼𝑐 𝑅1 + 𝐼5𝑅1 + 𝑢𝑐 = 𝐸1
𝑖5 𝑅5 − 𝑢𝑐 = 0
{
(19)
𝑖𝐿 𝑅46 + 𝑢𝐿 − 𝑖5 𝑅5 = 0
В (19) проводим замену переменных
𝑖𝐶 = 𝐶
𝑑𝑈𝐶
𝑑𝑖𝐿
и 𝑢𝐿 = 𝐿
𝑑𝑡
𝑑𝑡
(20)
Получаем искомую систему дифференциальных уравнений второго порядка
𝑖𝐿 𝑅1 + 𝐶
{
𝑑𝑈𝐶
𝑑𝑡
𝑅1 + 𝐼5𝑅1 + 𝑢𝑐 = 𝐸1
𝑖5 𝑅5 − 𝑢𝑐 = 0
𝑖𝐿 𝑅46 + 𝐿
𝑑𝑖𝐿
𝑑𝑡
(21)
− 𝑖5 𝑅5 = 0
2.5 Определение корней α1 и α2 характеристического уравнения
В общем случае решение системы уравнений (21) имеет вид (1) и (2).
Однако, следует отметить, что входящие в них установившиеся значения
величин 𝑈Суст и 𝐼𝐿уст уже определены (13). Остаются неизвестными только
свободные составляющие 𝑈𝐶св (𝑡) и 𝑖𝐿св (𝑡), значения которых не зависят от
величины E1. Они определяются энергией, накопленной в электрическом поле
емкости С и в магнитном поле индуктивности L. Отсюда, система уравнений
(21) для свободных составляющих принимает вид:
𝑖𝐿св 𝑅1 + 𝐶
{
𝑑𝑈𝐶св
𝑅1 + 𝐼5𝑅1 + 𝑢𝑐св = 𝐸1
𝑖5 𝑅5 − 𝑢𝑐св = 0
(22)
𝑑𝑡
𝑖𝐿св 𝑅46 + 𝐿
𝑑𝑖𝐿св
𝑑𝑡
− 𝑖5 𝑅5 = 0
Для решения дифференциальных уравнений используется прием по замене
символа дифференцирования
числа, тогда:
𝑑
𝑑𝑡
на величину α, обладающую свойствами
𝑖𝐿св 𝑅1 + 𝑈𝐶св 𝐶𝛼𝑅1 + 𝐼5𝑅1 + 𝑢𝑐св = 𝐸1
𝑖5 𝑅5 − 𝑢𝑐св = 0
{
(23)
𝑖𝐿св 𝑅46 + 𝑖𝐿св 𝐿𝛼 − 𝑖5 𝑅5 = 0
Согласно (23) составляем и раскрываем характеристический определитель
𝑢𝑐 св
(С𝛼𝑅1 + 1)
∆= |−1
0
𝑖𝐿св
𝑖5св
𝑅1
0
𝑅46 + 𝐿𝛼
−0,001485𝑎2 − 7,095𝑎 − 9150 = 0
𝑅1
𝑅5 | =
− 𝑅5
1
𝑐
1
𝑎2 = −2389 − 674,41𝑗
𝑐
𝑎1 = −2389 + 674,41𝑗
Корни
𝛼1
и 𝛼2
комплексно-сопряженные,
переходный
процесс
периодический.
2.6 Определение постоянных интегрирования (корни α1 и α2
комплексно-сопряженные)
В общем случае зависимость 𝒖𝑪 (𝒕) имеет вид:
𝒖𝑪 (𝒕) = 𝑼𝑪уст + 𝒖𝑪св (𝒕) = 𝑼𝑪уст + 𝑨𝒆−𝜹𝒕 𝐬𝐢𝐧(𝝎св 𝒕 + 𝝋𝑼𝑪 )
(𝟐𝟓)
где 𝑨, 𝝋𝑼𝑪 − искомые постоянные интегрирования; 𝝎𝟎 − резонансная
частота; 𝝎св − частота свободных затухающих колебаний;
Производная функции 𝒖𝑪 (𝒕)
𝑑𝑢𝐶 (𝑡)
= −𝐴 ∙ 𝛿 ∙ 𝑒 −𝛿𝑡 ∙ sin(𝜔св 𝑡 + 𝜑𝑈𝐶 ) + 𝐴 ∙ 𝑒 −𝛿𝑡 ∙ 𝜔св ∙ cos(𝜔св 𝑡 + 𝜑𝑈𝐶 ) (26)
𝑑𝑡
Записываем уравнения (25) и (26) при t=0+
𝑈𝐶+ = 𝑈𝐶 уст + 𝐴𝑠𝑖𝑛𝜑𝑈𝐶
{𝑑𝑢𝑐 (𝑡)
|
= −𝐴𝛿 ∙ sin 𝜑𝑈𝐶 + 𝐴 ∙ 𝜔св ∙ cos 𝜑𝑈𝐶
𝑑𝑡 𝑡=0+
(27)
Перепишем (32) в виде:
𝐴𝑠𝑖𝑛𝜑𝑈𝐶 = 𝑈𝐶+ − 𝑈𝐶 уст = 58,79 − 22,35 = 36,44 В
𝑑𝑢𝑐 (𝑡)
{
(28
𝐴 ∙ 𝜔св ∙ cos 𝜑𝑈𝐶 =
|
+ 𝐴𝛿 ∙ sin 𝜑𝑈𝐶 = 5000 − 36,44 ∙ 2389 = −82055,2
𝑑𝑡 𝑡=0+
где
𝑑𝑢𝑐 (𝑡)
𝑑𝑡
|
𝐼+
0,15
𝐶
30∙10−6
= 𝐶 =
+
𝑡=0
= 5000
Делим левые и правые части уравнений (28) и находим постоянную
интегрирования 𝜑𝑈𝐶 :
𝑡𝑔𝜑𝑈𝐶 =
36,44 ∙ 674,41
= −0,3; 𝜑𝑈𝐶 = −16,6° ;
−82055,2
Находим постоянную интегрирования A из (28):
𝐴=
36,44
= −127,55 В.
sin(−16,6° )
Итого, уравнение переходного процесса напряжения на емкости:
𝑢𝐶 (𝑡) = 22,35 − 127,55𝑒 −2389𝑡 ∙ 𝑠𝑖𝑛(674,41𝑡 − 16,6° ) В;
В общем случае зависимость 𝒊𝑳 (𝒕) имеет вид:
𝒊𝑳 (𝒕) = 𝑰𝑳уст + 𝒊𝑳св (𝒕)
= 𝑰𝑳уст + 𝑫𝒆−𝜹𝒕 𝐬𝐢𝐧(𝝎св 𝒕 + 𝝋𝒊𝑳 )
(𝟐𝟗)
Где 𝑫, 𝝋𝒊𝑳 − искомые постоянные интегрирования.
Производная функции 𝑖𝐿 (𝑡):
𝒅𝒊𝑳 (𝒕)
= −𝑫 ∙ 𝜹 ∙ 𝒆−𝜹𝒕 ∙ 𝐬𝐢𝐧(𝝎св 𝒕 + 𝝋𝒊𝑳 ) + 𝑫 ∙ 𝒆−𝜹𝒕 ∙ 𝝎св
𝒅𝒕
∙ 𝐜𝐨𝐬(𝝎св 𝒕 + 𝝋𝒊𝑳 ) (𝟑𝟎)
Записываем уравнения (36) и (37) при t=0+
𝐼𝐿+ = 𝐼𝐿 уст + 𝐷 ∙ 𝑠𝑖𝑛𝜑𝑖𝐿
{𝑑𝑖𝐿 (𝑡)
|
= −𝐷𝛿 ∙ sin 𝜑𝑖𝐿 + 𝐷 ∙ 𝜔св ∙ cos 𝜑𝑖𝐿
𝑑𝑡 𝑡=0+
(31)
Перепишем (38) в следующем виде:
𝐷 ∙ 𝑠𝑖𝑛𝜑𝑖𝐿 = 𝐼𝐿+ − 𝐼𝐿 уст = 0,28 − 0,53 = −0,25
𝑑𝑖𝐿 (𝑡)
{
𝐷 ∙ 𝜔св ∙ cos 𝜑𝑖𝐿 =
|
+ 𝐷𝛿 ∙ sin 𝜑𝑖𝐿 = 509,1 + (−0,25) ∗ (−2389) = −88,15
𝑑𝑡 𝑡=0+
где
𝑑𝑖𝐿 (𝑡)
𝑑𝑡
|
=
+
𝑡=0
𝑈𝐿+
𝐿
=
28
55∙10−3
= 509,1
Делим левые и правые части (32) и находим постоянную интегрирования 𝜑𝑖𝐿 :
𝑡𝑔𝜑𝑖𝐿 =
−0,25 ∙ 674,41
= 1,91; 𝜑𝑖𝐿 = 62,4°;
−88,15
Находим постоянную интегрирования D из (31):
𝐷=
−0,25
= −0,28 В.
sin(62,4°)
Итого, уравнение переходного процесса тока в индуктивности:
𝑖𝐿 (𝑡) = 0,53 − 0,28𝑒 −2389𝑡 𝑠𝑖𝑛(674,41𝑡 + 62,4°)
(33)
3. Компьютерное исследование переходного процесса в линейной
ЭЦ
3.1 Построение переходного процесса. (корни a1, a2 комплексносопряженные)
Построение графиков выполнено в Mathcad:
А) Напряжение на емкости С, В
Б) Ток на индуктивности L, А
Рисунок 11 - Переходный процесс в линейной ЭЦ, корни α1, α2 комплексносопряженные: а) 𝑢𝐶 (𝑡); б) 𝑢𝐿 (𝑡)
4. Заключение
В курсовом проекте проведено исследование эектрической цепи в трёх
режимах.
Первый этап включается в себя расчёт параметров ЭЦ с постоянным
источником тока (J1) и с гармночиеским источником ЭДС (E2). Результаты
расчетов проверены по балансу мощностей для постоянной цепи и векторным
диаграммам (рисунки 1,2) для гармночиеской цепи.
На втором этапе был произведён расчёт переходного процесса в цепи с
двумя источниками электрической энергии (ИЭЭ). Определены комплексно сопряженные корни харрактеристического уравнения переходного процесса:
𝑎1 = −2389 + 674,41𝑗
1
𝑐
𝑎2 = −2389 − 674,41𝑗
1
𝑐