
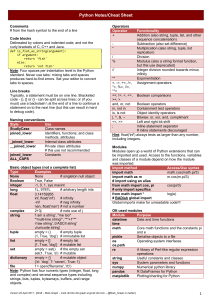
Python and Physics: RungeKutta Method
Luis Morales
·
Follow
Published in
CodeX
·
7 min read
·
Aug 19, 2021
--
1
One of the most commons math problems that I stumbled across in
grad school were Ordinary Differential Equations, otherwise known as
ODEs and one of the challenges that had me stumped for a while was,
how do I solve ODEs in Python? Thankfully, I was able to stumble
across two methods, the Runge-Kutta method and SciPy’s built-in
function.
Runge-Kutta Method
The Runge-Kutta method was a numerical approximation for ODE’s,
developed by Carl Runge and Wilhelm Kutta. By using four slope
values within an interval, that do not necessarily fall on the actual
solution, and averaging out the slopes, one can get a pretty nice
approximation of the solution. For a more in detail explanation of the
Runge-Kutta method and its variations, I highly suggest researching
the history, derivation and applications using your favorite
textbook/website. Now for this example, we will be focusing on the
Fourth Order Runge-Kutta Method to help us solve the 1D scattering
problem.
Coding
To start off our code, we are going to import some packages that will
help us with the math and the visualization.
import cmath #To help us out with the complex square root
import numpy as np #For the arrays
import matplotlib.pyplot as plt #Visualization
From here, we then start defining our initial parameters for the
equations.
mass = 1.0 #Mass, one for simplicity
hbar = 1.0 #HBar, one for simplicity
v0 = 2.0 #Initial potential value
alpha = 0.5 #Value for our potential equation
E = 3.0 #Energy
i = 1.0j #Defining imaginary number
x = 10.0 #Initial x-value
xf = -10.0 #Final x-value
h = -.001 #Step valuexaxis = np.array([], float) #Empty array to
fill with out x-valuespsi = np.array([], complex) #Empty array to
fill with the values for the initial equation we are trying to
solve, defined array as complex to fill with complex
numberspsiprime = np.array([], complex) #Empty array to fill with
the values for the first derivative equation we are trying to
solve, defined array as complex to fill with complex numbers
Once we have our initial values, we then start to work on our functions
that define the equations we are about to use. The main equation we
have is k(x), which is reworked version of Schrödinger's equation to
solve for the variable k, as well as our Ψ equations, which will be
defined by psione(x) and psitwo(x). To further explore the equation,
MIT OCW has free lectures that anyone can access for free.
def v(x): #Potential equation we will be using for this example
return v0/2.0 * (1.0 + np.tanh(x/alpha))def k(x): #Reworked
Schrödinger's equation to solve for k
return cmath.sqrt((2*mass/(hbar**2))*(E - v(x)))def psione(x):
#PSI, wavefunction equation
return np.exp(i*k(x)*x)def psitwo(x): #Derivative of the psione
equation
return i*k(x)*np.exp(i*k(x)*x)
Now this is where we get to the good part. First, we need to define an
array that contains our initial condition wavefunctions.
r = np.array([psione(x), psitwo(x)]) #Array with wavefunctions,
usually this is where our initial condition equations go.
With these equations set in our array, we can iterate both of these
equations through the Runge-Kutta method, which will be defined
below, and have them give us the approximate solutions for the
equation we defined for psione(x) and psitwo(x). But before we reach
the main part of the equation, we need to define one more important
function.
def deriv(r,x):
return np.array([r[1],-(2.0*mass/(hbar**2) * (E - v(x))*r[0])],
complex)
#The double star, **, is for exponents
The deriv function is where the outputs from the Runge-Kutta get
passed through, this function grabs our values from the array r and
then pushes it through these conditions. For the first value that gets
returned, it’s quite simple, our x value will just be inputted into the
second equation of the array. The second value, however, will be going
through a different treatment. This time, the x value will be going
through another iteration of Schrodinger’s equation, one that takes
into consideration the wave function psione(x).
#While loop to iterate through the Runge-Kutta. This particular
version, the Fourth Order, will have four slope values that help
approximate then next slope value, from k1 to k2, k2 to k3, and k3
to k4.#This loop also appends that values, starting with the
initial values, to the empty arrays that we've initialized
earlier.while (x >= xf ):
xaxis = np.append(xaxis, x)
psi = np.append(psi, r[0])
psiprime = np.append(psiprime, r[1])
k1 = h*deriv(r,x)
k2 = h*deriv(r+k1/2,x+h/2)
k3 = h*deriv(r+k2/2,x+h/2)
k4 = h*deriv(r+k3,x+h)
r += (k1+2*k2+2*k3+k4)/6
x += h #The += in this line, and the line above, is the
same thing as telling the code to x = x + h, which updates x, using
the previous x with the addition of the step value.
Here, the loop pretty much goes over the whole process of the RungeKutta. By using approximations of the slopes, as defined by
the k values, each k value helps approximate the next slope, bringing us
one step closer to solving for f(x). Furthermore, after getting each of
our slopes, we then obtain a weighted average and update our array
with these new values to get the ready for the next iteration. This
process will continue for our defined range in the x-axis, which will end
up giving us the necessary values for plotting our soon to be solved
ODE.
Overview
The Runge-Kutta Method can be easily adapted to plenty of other
equations, most of the time we just have to adjust the deriv function,
and our initial condition equations. Other examples include the
pendulum ODEs and planetary motion ODEs. Down below, one can
now find the full code, along with extra steps, such as the functions to
solve for the reflection and transmission values, as well as how to plot
our values.
import cmath #To help us out with the complex square root
import numpy as np #For the arrays
import matplotlib.pyplot as plt #Visualizationmass = 1.0 #Mass, one
for simplicity
hbar = 1.0 #HBar, one for simplicity
v0 = 2.0 #Initial potential value
alpha = 0.5 #Value for our potential equation
E = 3.0 #Energy
i = 1.0j #Defining imaginary number
x = 10.0 #Initial x-value
xf = -10.0 #Final x-value
h = -.001 #Step valuexaxis = np.array([], float) #Empty array to
fill with out x-valuespsi = np.array([], complex) #Empty array to
fill with the values for the initial equation we are trying to
solve, defined array as complex to fill with complex
numberspsiprime = np.array([], complex) #Empty array to fill with
the values for the first derivative equation we are trying to
solve, defined array as complex to fill with complex numbersdef
v(x): #Potential equation we will be using for this example
return v0/2.0 * (1.0 + np.tanh(x/alpha))def k(x): #Reworked
Schrödinger's equation to solve for k
return cmath.sqrt((2*mass/(hbar**2))*(E - v(x)))def psione(x):
#PSI, wavefunction equation
return np.exp(i*k(x)*x)def psitwo(x): #Derivative of the psione
equation
return i*k(x)*np.exp(i*k(x)*x)r = np.array([psione(x),
psitwo(x)]) #Array with wavefunctions, usually this is where our
initial condition equations go.def deriv(r,x):
return np.array([r[1],-(2.0*mass/(hbar**2) * (E - v(x))*r[0])],
complex)
#The double star, **, is for exponents#While loop to iterate
through the Runge-Kutta. This particular version, the Fourth Order,
will have four slope values that help approximate then next slope
value, from k1 to k2, k2 to k3, and k3 to k4.#This loop also
appends that values, starting with the initial values, to the empty
arrays that we've initialized earlier.while (x >= xf ):
xaxis = np.append(xaxis, x)
psi = np.append(psi, r[0])
psiprime = np.append(psiprime, r[1])
k1 = h*deriv(r,x)
k2 = h*deriv(r+k1/2,x+h/2)
k3 = h*deriv(r+k2/2,x+h/2)
k4 = h*deriv(r+k3,x+h)
r += (k1+2*k2+2*k3+k4)/6
x += h #The += in this line, and the line above, is the
same thing as telling the code to x = x + h, which updates x, using
the previous x with the addition of the step value.#Grabbing the
last values of the arrays and redefining our x-axis
psi1 = psi[20000]; psi2 = psiprime[20000]; x = 10; xf = -10def
reflection(x, y):
aa = (psi1 + psi2/(i*k(y)))/(2*np.exp(i*k(y)*y))
bb = (psi1 - psi2/(i*k(y)))/(2*np.exp(-i*k(y)*y))
return (np.abs(bb)/np.abs(aa))**2def transmission(x,y):
aa = (psi1 + psi2/(i*k(y)))/(2.0*np.exp(i*k(y)*y))
return k(x)/k(y) * 1.0/(np.abs(aa))**2print('reflection =
',reflection(x,xf))
print('transmission = ', transmission(x,xf))
print('r + t = ', reflection(x,xf) + transmission(x,xf))#Outputs
for the print command
#reflection = 0.007625630800891285
#transmission = (0.9923743691991354+0j)
#r + t = (1.0000000000000266+0j)
#Ideally, r + t should give us one, a bit stumped if the precision
that's present in Python can lead to the small discrepancy, without
considering formatting the answer to a set amount of decimal
values.#Plotting the graphs side by side, including the imaginary
values.fig, ax = plt.subplots(1,2, figsize = (15,5))
ax[0].plot(xaxis, psi.real, xaxis, psi.imag, xaxis, v(xaxis))
ax[1].plot(xaxis, psiprime.real, xaxis, psiprime.imag, xaxis,
v(xaxis))
plt.show()
Visual Output for this code. Note how the wavefunction changes as it enters the potential barrier.
For those interested in the built-in SciPy version of this code, here you
go.
import cmath
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint, solve_ivpE = 3; m = 1; h = 1;
alpha = .5; v0=2; i = 1.0j; xi = 10; xf = -10def v(x): return
v0/2.0 * (1.0 + np.tanh(x/alpha))def k(x): return
cmath.sqrt((2*m/(h**2))*(E - v(x)))def psione(x): return
np.exp(i*k(x)*x)def psitwo(x): return i*k(x)*np.exp(i*k(x)*x)def
deriv(x, y): return [y[1], -(2.0*m/(h**2.0) * (E - v(x))*y[0])]#
solve_ivp is a built in rk45step solver
values = solve_ivp(deriv, [10, -10], [psione(xi), psitwo(xi)],
first_step = .001, max_step = .001)psi1 = values.y[0,20000]; psi2 =
values.y[1,20000]; x = 10; xf = -10def reflection(x, y):
aa = (psi1 + psi2/(i*k(y)))/(2*np.exp(i*k(y)*y))
bb = (psi1 - psi2/(i*k(y)))/(2*np.exp(-i*k(y)*y))
return (np.abs(bb)/np.abs(aa))**2def transmission(x,y):
aa = (psi1 + psi2/(i*k(y)))/(2.0*np.exp(i*k(y)*y))
return k(x)/k(y) * 1.0/(np.abs(aa))**2print('reflection =
',reflection(x,xf))
print('transmission = ', transmission(x,xf))
print('r + t = ', reflection(x,xf) + transmission(x,xf))fig, ax =
plt.subplots(1,2, figsize = (15,5))
ax[0].plot(values.t, values.y[0].real, values.t, values.y[0].imag,
values.t, v(values.t))
ax[1].plot(values.t, values.y[1].real, values.t, values.y[1].imag,
values.t, v(values.t))
plt.show()
Notes
A bit of a disclaimer, most of this code was adapted from the
coursework from my computational class, which focused on using
FORTRAN90 instead of Python, so code may not be efficient since I
started teaching myself Python by transferring code from FORTRAN.
Plus, a nice shoutout to MIT OCW for giving me a small refresher on
the equations and methods used in this code.





![Foundational Python for Data Science [2022] Kennedy R. Behrman](http://s1.studylib.ru/store/data/006557552_1-250ad428194058cca240f6cf36a7dd4d-300x300.png)

