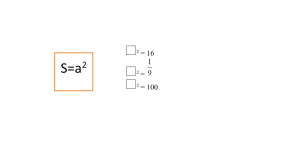
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ y = И ПРИМЕНЕНИЕ ЕЁ СВОЙСТВ x Цели: изучить функцию y = x , её график и свойства; формировать умение строить график этой функции и применять её свойства. Ход урока I. Организационный момент. II. Устная работа. 1. Решите уравнение: 1 б) х2 = 49 ; а) х2 = 16; 1 4; г) х2 = 2. Вычислите: а) в) х2 = 0; 2 е) х2 = 3 . д) х2 = 10; 36 ; б) 1 81 ; в) 40000 ; 2 49 г) 121 ; д) 0,0025 ; 2 7 е) . III. Объяснение нового материала. Объяснение проводится согласно пункту учебника. 1) Рассмотреть, из каких практических ситуаций возникает потребность в изучении функции y = x. 2) Составить таблицу значений функции y = 3) Перечислить свойства функции y = x и построить её график. x. 4) Сопоставить графики функций у = х2 и y = x. IV. Формирование умений и навыков. Все з а д а н и я, которые должны быть выполнены учащимися на этом уроке, можно условно разбить на т р и г р у п п ы: выражение из различных формул зависимости вида y = x; x и его «чтение»; применение свойства возрастания функции y = x для сравнения квадратных построение графика функции y = корней. 1-я г р у п п а. 1. № 352.(345) 2. № 354.(347) Решение S = 4πR2 S R2 = 4 S R = 4 2-я г р у п п а. 1. № 355. 2. № 357. 3-я г р у п п а. x сравните числа: 1 6 3; в) 3,6 и 2 9 5 и 7,1 . г) 1. С помощью графика функции y = а) 0,7 и 1; б) 3 и 7,5 ; 2. № 364. Решение Учащиеся должны воспользоваться следующим свойством функции y = x : большему значению аргумента соответствуют большие значения функции. При сравнении квадратного корня с рациональным числом можно это число записать в виде корня. 27 < 28 ; б) 1,3 < 1,5 ; в) 7 < 9 , то есть 7 < 3; г) 6,25 = 6,25 , то есть 6,25 = 2,5; 1 1 д) 5 > 6 . а) V. Итоги урока. В о п р о с ы у ч а щ и м с я: – Что называется арифметическим квадратным корнем из числа а? – Как построить график функции y = x? – Какими свойствами обладает функция y = x? – Как располагаются относительно друг друга графики функций у = х2 и y = 0? Домашнее задание: № 353, № 356, № 363. (346, 349, 356) x при х ≥