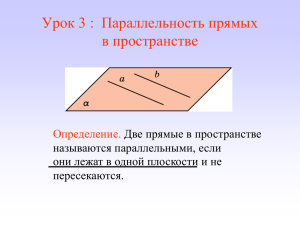
Каратанова М.Н. МБОУ СОШ №256 ГО ЗАТО Фокино Приморский кр. Взаимное расположение прямых в пространстве. пересекаются Лежат в одной плоскости Не лежат в одной плоскости скрещиваются параллельны b b а а b а Параллельными называются прямые, лежащие в одной плоскости и не имеющие точек пересечения. Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. a К b Параллельные отрезки, параллельные лучи в пространстве. • Отрезки в пространстве называются параллельными, если … • Лучи в пространстве называются параллельными, если … …они лежат на параллельных прямых Лемма о параллельных прямых Если одна из параллельных прямых пересекает плоскость, то и вторая прямая также пересекает эту плоскость? a b α в •В в1 а β с Две прямые, параллельные третьей прямой, параллельны Доказательство: 1 случай. а, в, с α рассмотрен в планиметрии 2 случай. а, в α; а, с β 1. Возьмем т.В, В в Через т.В и с проведем плоскость 2. Если в1 β = Х, Х а, в1 α, но Х с, т.к. в1 , α = в1 а т.к. а с в1 β 3. в1 α, в1 а в1 а в1 = в (А параллельных прямых) 4. в с Теорема доказана. Теорема о параллельных прямых. a К b Дано: К a Доказать: ! b: К b, b a Доказательство: 1.Проведем через прямую a и точку К плоскость α. 2.Проведем через т. К α прямую b, b a.(А планиметрии) Единственность (от противного) 1.Пусть b1: К b1 , b1 a .Через прямые a и b1 можно провести плоскость α1. 2. a , К α1; α1 и α (Т о точке и прямой в пространстве). 3. b = b1 (А параллельных прямых). Теорема доказана. Задание 1 Вставьте пропущенные слова 1) Единственную плоскость можно задать через три точки, при этом они не лежат на одной прямой. 2) Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости. 3) Две различные плоскости могут иметь только одну общую прямую 4) Прямые являются параллельными в пространстве, если они не пересекаются и лежат в одной плоскости. 5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке В α, то прямые а и b скрещивающиеся Задание 2 Определите: верно, ли утверждение? 1. Если прямая проходит через вершину Нет треугольника, то она лежит в плоскости треугольника. 2. Если прямые не пересекаются, то они Нет параллельны. 3. Прямая m параллельна прямой n, прямая m Да параллельна плоскости α. Прямая n параллельна плоскости α. 4. Все прямые пересекающие стороны Да треугольника лежат в одной плоскости. 5. Прямая АВ и точки С, D не лежат в одной Нет плоскости. Могут ли прямые АВ и СD пересекаться? Задание 2 Определите: верно, ли утверждение? 6. Прямые АВ и СD пересекаются. Могут ли прямые АС и ВD быть скрещивающимися? 7. Прямые а и в не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и в? 8. Прямая а, параллельная прямой в, пересекает плоскость α. Прямая с параллельна прямой в. Может ли прямая с лежать в плоскости α? 9. Прямая а параллельна плоскости α. Существует ли на плоскости α прямые, непараллельные а? Нет Нет Нет Да 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Точки М и К принадлежат рёбрам ВВ₁ и СС₁ куба ABCDA₁B₁C₁D₁. Точка Т лежит на прямой МК. Какой плоскости принадлежит точка Т? А₁С₁D₁ CDC₁ BB₁C₁ . T B₁ А₁ . C₁ M D₁ AA₁B₁ . K В C А D 1 Точки М и К принадлежат рёбрам ВВ₁ и АВ куба ABCDA₁B₁C₁D₁. Точка Т лежит на прямой МК. Какой плоскости принадлежит точка Т? B₁ А₁С₁D₁ CDC₁ ВВ₁С₁ . T C₁ А₁ АА₁В₁ D₁ M А . . В C K D 2 Точки М и N являются серединами рёбер AВ и ВC пирамиды DABC. По какой прямой пересекаются плоскости BDM и ACN? D АD MN АВ BN . M А C . N 3 В Точки М и N являются серединами рёбер AВ и ВD пирамиды DABC. По какой прямой пересекаются плоскости BDM и BCN? D ВD АB MN . N BC . M А В C 4 Точки A и B принадлежат рёбрам MN и MM₁ куба KLMNK₁L₁M₁N₁. Через какие указанные точки можно провести единственную плоскость? M₁ N₁ N, A, M L₁ B, M, M₁ K₁ . B N, A, L . A M L K 5 N Точки A и B принадлежат рёбрам MN и MM₁ куба KLMNK₁L₁M₁N₁. Через какие указанные точки можно провести единственную плоскость? . M₁ N₁ B A, B, M L₁ K₁ B, L₁, M₁ A, L, L₁ . A M N L K 6 Вершина D квадрата ABCD принадлежит плоскости β, а остальные его вершины не принадлежат плоскости β. Как расположены прямые AB и BC относительно β? B АВ ∩ β, ВС ∩ β АВ ∩ β, ВС ∩ β A C АВ ∩ β, ВС ∩ β АВ ∩ β, ВС ∩ β β . D 7 Вершина А параллелограмма принадлежит плоскости β, а остальные его вершины не принадлежат плоскости β. Как расположены прямые СB и CD относительно β? C CВ ∩ β, СD ∩ β CВ ∩ β, СD ∩ β B CВ ∩ β, СD ∩ β CВ ∩ β, СD ∩ β β D . A 8 Угол ABС лежит в плоскости α, точка К не принадлежит плоскости α . Сколько прямых, параллельных сторонам угла, можно провести через точку К? . ОТВЕТ 2 К С A α B 9 Треугольник ABС лежит в плоскости α, точка М не принадлежит плоскости α . Сколько прямых, параллельных сторонам тр-ка, можно провести через М? . М ОТВЕТ 3 С A α B 10 Сторона AB лежит в плоскости α, точка К не принадлежит плоскости α . Сколько прямых, параллельных сторонам угла АВС, можно провести через точку К? . С К ОТВЕТ 2 A B 11 α Точка М принадлежит ребру SВ пирамиды SABC. Сколько прямых, параллельных рёбрам пирамиды, можно провести через точку М? S . M ОТВЕТ 5 А В C 12 Точка М принадлежит грани SВС пирамиды SABC. Сколько прямых, параллельных рёбрам пирамиды, можно провести через точку М? S . M ОТВЕТ 6 А В C 13 Точки К и L лежат на прямых PN и PM, пересекающих плоскость α в точках N и M; PK : KN = PL : LM = 2 : 3, KL = 12. Найдите расстояние между точками N и M? P К ОТВЕТ 30 . . L N M 14 α Точки N и L лежат на прямых AB и AC, пересекающих плоскость α в точках B и C; AN : NB = AL : LC = 4 : 1, NL = 60. Найдите расстояние между точками B и C? A ОТВЕТ 75 . N B . L C α 15 Дано: ∆АВК; АВ ll ; (АВК)∩ = СD; СK = 8; АВ = 7; АС = 6 Доказать: АВ ll СD Найти: СD В А С D K Дано: ∆АВС; АВ ∩ = В1; АС ∩ = С1; ВС ll ; АВ : ВВ1 = 8 : 3; АС = 16 см Доказать: ВC llB1С1 А Найти: АС1 В В1 С1 С Точка C лежит на отрезке AB. Через точку A проведена плоскость, а через точки В и С параллельные прямые, пересекающие эту плоскость соответственно в точках B1 и C1. Найдите длину отрезка СC1, если АС:СB = 3:2 и BB1 = 20 см. Источники Титульный слайд Фон слайдов