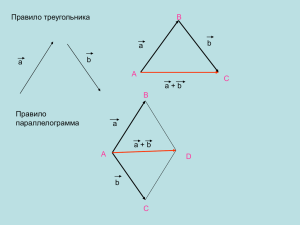
Практическое занятие № ___ Учебная дисциплина: математика Вид занятия: практический Курс __ Группа _____ Преподаватель: __________ Дата______ Тема занятия: Сложение и вычитание векторов. Цели занятия: Образовательные: обобщение и систематизация знаний Развивающие: расширение кругозора студентов при решении практических задач Воспитательные: воспитание интереса к предмету через умение видеть прекрасное и пропорциональности окружающего мира Задачи занятия: Повторить, обобщить и систематизировать знания о векторах. Задания: Выполнить практические задания Методические указания и порядок выполнения задания Сложение и вычитание векторов. Сумма двух векторов. Законы сложения векторов. Правило параллелограмма. Правило треугольника. ⃗ и ⃗𝒃, нужно: Чтобы найти вектор суммы двух векторов 𝒂 ⃗; 1) совместить параллельным переносом начало вектора ⃗𝒃 с концом вектора 𝒂 ⃗; ⃗ в конец вектора 𝒃 2) провести вектор из начала вектора 𝒂 ⃗ + ⃗𝒃. 3) получившийся вектор и есть вектор суммы: 𝒂 Если к вектору 𝑎 прибавить нулевой вектор ⃗0 по правилу треугольника, то получим ⃗ =𝒂 ⃗ +𝟎 ⃗. вектор 𝑎, т.е. справедливо равенство: 𝒂 Утверждение. Если 𝑨, 𝑩 и 𝑪 – произвольные точки, то ⃗⃗⃗⃗⃗⃗ 𝑨𝑩 + ⃗⃗⃗⃗⃗⃗ 𝑩𝑪 = ⃗⃗⃗⃗⃗ 𝑨𝑪. ⃗⃗⃗ ⃗⃗⃗𝒃 и 𝒄 ⃗ справедливы равенства: ТЕОРЕМА. Для любых векторов 𝒂, ⃗ =𝒃 ⃗ +𝒂 ⃗ +𝒃 ⃗ (переместительный закон) 𝒂 ⃗ )+𝒄 ⃗ +𝒄 ⃗ +𝒃 ⃗ =𝒂 ⃗ + (𝒃 ⃗ ) (сочетательный закон). (𝒂 Дано: 𝑎, 𝑏⃗, 𝑐 Доказать: 1) 𝑎 + 𝑏⃗ = 𝑏⃗ + 𝑎 2) (𝑎 + 𝑏⃗) + 𝑐 = 𝑎 + (𝑏⃗ + 𝑐 ) Доказательство. Доказательство теоремы в случае, когда векторы коллинеарны достаточно простое. Его вы можете провести самостоятельно. Мы рассмотрим случай, когда данные векторы неколлинеарны. 1). Отметим произвольную точку 𝐴 и отложим от этой точки вектор ⃗⃗⃗⃗⃗ 𝐴𝐵 = 𝑎. ⃗ ⃗⃗⃗⃗⃗ Воспользуемся правилом треугольника и прибавим к нему вектор 𝐵𝐶 = 𝑏. Вектором суммы этих двух векторов является вектор ⃗⃗⃗⃗⃗ 𝐴𝐶 = 𝑎 + 𝑏⃗. (Рисунок слева). Теперь от точки 𝐴 и отложим вектор ⃗⃗⃗⃗⃗ 𝐴𝐾 = 𝑏⃗ . По правилу треугольника прибавим к нему ⃗⃗⃗⃗⃗⃗ = 𝑏⃗ + 𝑎 . ⃗⃗⃗⃗⃗⃗⃗ = 𝑎 . Вектором суммы этих двух векторов является вектор 𝐴𝑀 вектор 𝐾𝑀 (Рисунок справа). ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ = 𝑏⃗, значит, они сонаправлены и длины у них равны; 𝐴𝐾 = 𝐵𝐶 | ⟹ 𝐴𝐵𝐶𝐾 – ⃗⃗⃗⃗⃗ = 𝑎, значит, они тоже сонаправлены и длины у них равны; ⃗⃗⃗⃗⃗⃗⃗ = 𝐴𝐵 𝐾𝑀 ⃗⃗⃗⃗⃗ = 𝐴𝑀 ⃗⃗⃗⃗⃗⃗ , т.е. 𝑎 + 𝑏⃗ = 𝑏⃗ + 𝑎. параллелограмм и точка 𝑀 совпадает с точкой 𝐶. Значит, 𝐴𝐶 ⃗⃗⃗⃗⃗ = 𝑏⃗, а от 2). От точки 𝐴 отложим вектор ⃗⃗⃗⃗⃗ 𝐴𝐵 = 𝑎, от точки 𝐵 отложим вектор 𝐵𝐶 точки 𝐶 – вектор ⃗⃗⃗⃗⃗ 𝐶𝐷 = 𝑐. Найдём суммы векторов по правилу треугольника. ⃗⃗⃗⃗⃗ + 𝐵𝐶 ⃗⃗⃗⃗⃗ ) + ⃗⃗⃗⃗⃗ (𝑎 + 𝑏⃗) + 𝑐 = (𝐴𝐵 𝐶𝐷 = ⃗⃗⃗⃗⃗ 𝐴𝐶 + ⃗⃗⃗⃗⃗ 𝐶𝐷 = ⃗⃗⃗⃗⃗ 𝐴𝐷 ; | ⟹ (𝑎 + 𝑏⃗) + 𝑐 = 𝑎 + (𝑏⃗ + 𝑐 ). ⃗⃗⃗⃗⃗ + ⃗⃗⃗⃗⃗ 𝑎 + (𝑏⃗ + 𝑐 ) = ⃗⃗⃗⃗⃗ 𝐴𝐵 + (𝐵𝐶 𝐶𝐷) = ⃗⃗⃗⃗⃗ 𝐴𝐵 + ⃗⃗⃗⃗⃗⃗ 𝐵𝐷 = ⃗⃗⃗⃗⃗ 𝐴𝐷 ; Теорема доказана. При доказательстве первой формулы получился параллелограмм, причём, из точки 𝐴 выходят два вектора 𝑎 и 𝑏⃗, а вектор их суммы является диагональю параллелограмма. На основе этого возникает второе правило геометрического сложения векторов. Правило параллелограмма. ⃗ , нужно: ⃗ и𝒃 Чтобы найти вектор суммы двух векторов 𝒂 ⃗; ⃗ и 𝒃 1) совместить параллельным переносом начала векторов 𝒂 2) на этих векторах достроить параллелограмм; ⃗ является вектор, который лежит на диагонали ⃗ +𝒃 3) вектором суммы 𝒂 параллелограмма, имеющий своё начало в начале исходных векторов. Сумма нескольких векторов. Сложение нескольких векторов происходит по принципу правила треугольника. Складываются два вектора, к вектору суммы прибавляется следующий вектор и т.д. Приведём пример. Сложить векторы 𝑎, 𝑏⃗, 𝑐 , 𝑑, 𝑓 . ⃗⃗⃗⃗⃗ = 𝑎. Отметим точку 𝐴 и отложим от неё вектор 𝐴𝐵 ⃗⃗⃗⃗⃗ = 𝑏⃗ по правилу Прибавим к нему вектор 𝐵𝐶 ⃗⃗⃗⃗⃗ + 𝐵𝐶 ⃗⃗⃗⃗⃗ = 𝐴𝐶 ⃗⃗⃗⃗⃗ . Теперь к вектору 𝐴𝐶 ⃗⃗⃗⃗⃗ треугольника. 𝐴𝐵 прибавим вектор ⃗⃗⃗⃗⃗ 𝐶𝐷 = 𝑐 . ⃗⃗⃗⃗⃗ 𝐴𝐶 + ⃗⃗⃗⃗⃗ 𝐶𝐷 = ⃗⃗⃗⃗⃗ 𝐴𝐷 . К вектору ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ 𝐴𝐷 прибавляем вектор 𝐷𝐹 = 𝑑 . 𝐴𝐷 + ⃗⃗⃗⃗⃗ 𝐷𝐹 = ⃗⃗⃗⃗⃗ 𝐴𝐹 . ⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ Осталось к вектору 𝐴𝐹 прибавить вектор 𝐹𝐸 = 𝑓 . ⃗⃗⃗⃗⃗ 𝐴𝐹 + ⃗⃗⃗⃗⃗ 𝐹𝐸 = ⃗⃗⃗⃗⃗ 𝐴𝐸 . ⃗⃗⃗⃗⃗ + 𝐵𝐶 ⃗⃗⃗⃗⃗ + 𝐶𝐷 ⃗⃗⃗⃗⃗ + 𝐷𝐹 ⃗⃗⃗⃗⃗ + ⃗⃗⃗⃗⃗ Итак, 𝐴𝐵 𝐹𝐸 = ⃗⃗⃗⃗⃗ 𝐴𝐸 . Значит, суммой векторов 𝑎 + 𝑏⃗ + 𝑐 + 𝑑 + 𝑓 является вектор, с началом в начале первого вектора и концом – в конце последнего. Такое сложение векторов называется правилом многоугольника. Правило многоугольника. Чтобы найти вектор суммы нескольких векторов, нужно: 1) последовательно совместить параллельным переносом начало последующего вектора с концом предыдущего; 2) вектором суммы всех векторов является вектор, с началом в начале первого вектора и концом – в конце последнего. ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝟏 𝑨𝟐 + ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝟐 𝑨𝟑 + ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝟑 𝑨𝟒 + ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝟒 𝑨𝟓 + … + ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝒏−𝟐 𝑨𝒏−𝟏 + ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝒏−𝟏 𝑨𝒏 = ⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ 𝑨𝟏 𝑨𝒏 Вычитание векторов. Определение. Разностью двух векторов 𝑎 и 𝑏⃗ называется такой вектор 𝑐 , что при сложении его с вектором 𝑏⃗ получается вектор 𝑎. ⃗ =𝒄 ⃗ =𝒂 ⃗ −𝒃 ⃗ ⟹𝒄 ⃗ +𝒃 ⃗ 𝒂 Вычитание векторов можно производить, руководствуясь двумя понятиями: следствием из правила треугольника сложения векторов; определением разности двух чисел. Разберём каждое из них. Сложим векторы 𝑎 и 𝑏⃗ по правилу треугольника. По рисунку видно, ⃗⃗⃗⃗⃗ + 𝐵𝐶 ⃗⃗⃗⃗⃗ = 𝐴𝐶 ⃗⃗⃗⃗⃗ . Отсюда, 𝐵𝐶 ⃗⃗⃗⃗⃗ = 𝐴𝐶 ⃗⃗⃗⃗⃗ − 𝐴𝐵 ⃗⃗⃗⃗⃗ и 𝐴𝐵 ⃗⃗⃗⃗⃗ = 𝐴𝐶 ⃗⃗⃗⃗⃗ − 𝐵𝐶 ⃗⃗⃗⃗⃗ . Значит, что 𝐴𝐵 разность двух векторов можно составить, совмещая их начала, либо совмещая их концы. Отсюда два правила: I правило вычитания векторов. Чтобы найти вектор разности двух векторов, нужно: 1) совместить параллельным переносом начала этих векторов; 2) вектором разности является вектор с началом в конце второго вектора и концом в конце первого вектора. ⃗⃗⃗⃗⃗⃗ = 𝑨𝑪 ⃗⃗⃗⃗⃗ − 𝑨𝑩 ⃗⃗⃗⃗⃗⃗ 𝑩𝑪 II правило вычитания векторов. Чтобы найти вектор разности двух векторов, нужно: 1) совместить параллельным переносом концы этих векторов; 2) вектором разности является вектор с началом в начале первого вектора и концом в начале второго вектора. ⃗⃗⃗⃗⃗ − 𝑩𝑪 ⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗⃗ = 𝑨𝑪 𝑨𝑩 Далее, из алгебры мы знаем, что для того, чтобы из числа 𝑎 вычесть число 𝑏, нужно к числу 𝑎 прибавить число, противоположное числу 𝑏, т.е. 𝑎 − 𝑏 = 𝑎 + (−𝑏). Такое же правило справедливо и для векторов. ⃗⃗⃗ ⃗⃗⃗𝒃 справедливо равенство: ТЕОРЕМА. Для любых векторов 𝒂, ⃗ =𝒂 ⃗) ⃗ −𝒃 ⃗ + (−𝒃 𝒂 Дано: 𝑎, 𝑏⃗ Доказать: 𝑎 − 𝑏⃗ = 𝑎 + (−𝑏⃗) Доказательство. 1. Найдём разность векторов 𝑎 − 𝑏⃗ по I правилу. Вектором разности является вектор 𝑐 (рисунок слева). А теперь найдём сумму векторов 𝑎 + (−𝑏⃗) по правилу треугольника, где −𝑏⃗ – вектор, противоположный вектору 𝑏⃗. Вектором суммы является вектор ⃗⃗𝑐′ (рисунок справа). Не трудно заметить, что ⃗⃗𝑐′ = 𝑐 . Они сонаправлены и имеют одинаковые модули. 2. А теперь докажем то же самое аналитически. По определению разности векторов, (𝑎 − 𝑏⃗) + 𝑏⃗ = 𝑎 (𝑎 − 𝑏⃗) + 𝑏⃗ + (−𝑏⃗) = 𝑎 + (−𝑏⃗) (𝑎 − 𝑏⃗) + ⃗0 = 𝑎 + (−𝑏⃗) 𝑎 − 𝑏⃗ = 𝑎 + (−𝑏⃗) Что и требовалось доказать. Из этой теоремы следует третье правило вычитания векторов. III правило вычитания векторов. Чтобы найти вектор разности двух векторов, нужно к первому вектору прибавить вектор, противоположный второму. Используя это правило вычитания векторов, способ сложения векторов выбирается произвольно. Практические задания. 1. Вектор 𝑐 является суммой векторов 𝑎 и 𝑏⃗. Определите, какой из четырёх рисунков верный. ⃗⃗⃗⃗⃗ , 𝐵𝐶 ⃗⃗⃗⃗⃗ , 𝐶𝐷 ⃗⃗⃗⃗⃗ , 𝐷𝐴 ⃗⃗⃗⃗⃗ . Какая геометрическая фигура у вас получилась? 2. Проведите векторы 𝐴𝐵 3. Вектор 𝑐 является разностью векторов 𝑎 и 𝑏⃗. Определите, какой из четырёх рисунков верный. 4. Вектор 𝑐 является суммой векторов 𝑎 и 𝑏⃗. Определите, какой из четырёх рисунков верный. 5. Упростите выражения: ⃗⃗⃗⃗⃗ + 𝐻𝐾 ⃗⃗⃗⃗⃗⃗⃗ ⃗⃗⃗⃗⃗ + 𝐾𝑃 ⃗⃗⃗⃗⃗⃗ + 𝐶𝐻; ⃗⃗⃗⃗⃗⃗⃗ − 𝐴𝑃 ⃗⃗⃗⃗⃗ ; а) 𝐴𝐶 б) ⃗⃗⃗⃗⃗⃗ 𝐴𝑀 − 𝐾𝑀 ⃗⃗⃗⃗⃗ + 𝐶𝑀 ⃗⃗⃗⃗⃗⃗ + 𝐵𝐶 ⃗⃗⃗⃗⃗ ; ⃗⃗⃗⃗⃗⃗ − 𝑁𝑀 ⃗⃗⃗⃗⃗ ; ⃗⃗⃗⃗⃗⃗⃗ − 𝐴𝑃 в) 𝐴𝐵 г) 𝐴𝑀 ⃗⃗⃗⃗⃗⃗ + 𝑃𝐴 ⃗⃗⃗⃗⃗ + 𝑀𝑃 ⃗⃗⃗⃗⃗⃗ − 𝐻𝐾 ⃗⃗⃗⃗⃗ . ⃗⃗⃗⃗⃗⃗ ; ⃗⃗⃗⃗⃗⃗ − 𝐴𝐾 д) 𝐶𝑀 е) 𝐴𝑀 6. Длина вектора 𝑎 равна 5, а длина вектора 𝑐 равна 11. Сколько различных целых значений может принимать длина вектора (𝑎 + 𝑐 )? Литература 1. Богомолов Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для среднего профессионального образования / Н. В. Богомолов. — 11-е изд., перераб. и доп. — Москва : Издательство Юрайт, 2021. — 326 с. — (Профессиональное образование). — ISBN 978-5534-08799-4. — Текст : электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/470650. 2. Богомолов Н. В. Практические занятия по математике в 2 ч. Часть 2 : учебное пособие для среднего профессионального образования / Н. В. Богомолов. — 11-е изд., перераб. и доп. — Москва : Издательство Юрайт, 2021. — 251 с. — (Профессиональное образование). — ISBN 978-5534-08803-8. — Текст : электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/470651. 3.Башмаков М.И. Математика.: учебник – Москва: Издательский центр» Академия». 2021.- 256 с. Интернет – ресурсы: 1. Единое окно доступа к образовательным ресурсам. Электронная библиотека [Электронный ресурс]. — Режим доступа: http://window.edu.ru/window, свободный. — Загл. с экрана. Домашнее задание. Выполнить практические задания. Обратная связь: Выполненное задание отправить : Телеграмм, e-mail [email protected] Консультации по телефону+79497083715