Физика 2лабx
реклама

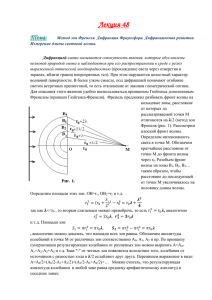
СПб НИУ ИТМО кафедра ИПМ Физика Лабораторная работа № 2 Определение длины световой волны по картине дифракции на круглом отверстии. Работу выполнил: Студент II курса Группы № 2120 Журавлев Виталий Преподаватель: Музыченко Я. Б. Санкт-Петербург 2013 г. Цель работы: Определение длины световой волны по картине дифракции на круглом отверстии. Общие положения: При прохождении пучка параллельных лучей света через круглое отверстие в экране свет заходит в область геометрической тени. За экраном наблюдается дифракционная картина в виде чередующихся светлых и тёмных колец. Распределение интенсивности света в дифракционной картине можно рассчитать на основе принципа Гюйгенса-Френеля, через метод зон Френеля. Пусть на экран с круглым отверстием радиусом OB падает плоская монохроматическая волна (рис. 1). В соответствии с принципом Гюйгенса-Френеля действие этой волны можно заменить действием когерентных точечных источников света. Определим действие этой волны в точке P, лежащей на прямой SS′, проходящей через центр отверстия. Для этого разделим часть волновой поверхности на кольцевые зоны (зоны Френеля), чтобы расстояния от края следующей зоны до точки P λ отличались друг от друга на половину длины волны 2: 𝑟1 = 𝑟0 + 𝜆 2 ; 𝑟2 = 𝑟1 + 𝜆 2 𝜆 Рис. 1 𝜆 = 𝑟0 + 2 2 ; … ; 𝑟𝐾 = 𝑟0 + к 2. (1) При таком делении фазы колебаний, приходящих в точку P от соседних зон, отличаются на , т.е. противоположны. Если амплитуды колебаний от 1, 2,…,к-ой зон обозначить a1, a2, … , aK , то амплитуда результирующего колебания в точке P: 𝐴 = 𝑎1 – 𝑎2 + 𝑎3 – 𝑎4 + … + (−1)𝐾 + 1𝑎к. (2) Амплитуда колебаний, приходящих от отдельной зоны, зависит от площади зоны ΔS, от расстояния rK от зоны до точки P и от угла наклона между rK и нормалью к поверхности. При при таком способе деления площадь K-ой зоны: SK K2 1 K2 (K2 1 K2 ) , (3) где K 1 и K – радиусы (K+1)-й и K-й зон. Радиусы зон Френеля определяются соотношениями: K2 (r0 к )2 r02 2 и K2 1 (r0 (к 1) )2 r02 Учитывая, что r0 >> λ, получим S K r0 2 . (4) K2 1 K2 r0 , а площадь K-й зоны , т.е. площадь зоны Френеля не зависит от номера зоны K. Следовательно, амплитуды колебаний зависят лишь от расстояния r и от угла . Монотонное убывание амплитуд позволяет приближенно выразить амплитуду A суммарного колебания в точке P: A a a a1 a1 a a ( a2 3 ) ( 3 a4 5 ) ( 5 ... 2 2 2 2 2 2 . (5) Так как слагаемые, выделенные скобками, равны нулю, результирующая амплитуда при нечетном K: Объединяя, получаем A a1 aK a a A 1 K 2 2 , а при четном K: 2 2 . A a1 aK 2 2 , где знак “+” относится к нечетному, а знак ““ – к четному числу зон Френеля. При свободном распространении, когда не происходит ограничение фронта волны, к → ∞ и aK → 0. Тогда при открытом фронте амплитуда суммарного колебания в точке P определяется половиной амплитуды первой зоны. Если отверстие открывает одну зону или их небольшое нечетное число, то в результате интерференции в точке P будет виден свет, причем более интенсивный, т.е. образуется дифракционный максимум. При небольшом четном числе открытых зон освещенность в точке P будет минимальной. Пусть для точки наблюдения P открыто m зон. Тогда при соблюдении предложенного Френелем правила разбиения на зоны, в открытой отверстием части волнового фронта будет умещаться большее число зон. R2 md . (6) Из выражения (6) расстояние от плоскости отверстия до точки наблюдения: d R2 m . (7) Это соотношение служит для вычисления длины волны. Для повышения точности определения длины волны расстояние d измеряется несколько раз при 1 разном числе открытых зон m. Как видно из уравнения (7), зависимость d от 𝑚 является линейной, а коэффициент наклона графика этой зависимости 𝑘 = 1 𝑅2 λ . Построив график зависимости d от 𝑚 можно убедиться в том, что зависимость действительно линейна, а по коэффициенту наклона получившейся прямой и известному значению радиуса отверстия R определить длину волны. Обработка результатов: Координата объектива в области действия законов геометрической оптики: 𝑋 = 83,4 см Координаты объектива при дифракционной картине от отверстия, соответствующего открытым m зонам Френеля: таблица 1 m Хо1 2 64,0 3 70,5 4 73,6 5 75,7 6 77,0 Хо2 64,7 70,1 73,4 75,6 77,0 Хо3 64,5 70,7 73,5 75,7 77,1 Расстояние от плоскости отверстия до точки наблюдения: 𝑑 = 𝑙 − 𝑏 = 𝑥 - − 𝑥 Результаты расчетов расстояния d для каждого m: таблица 2 m d1 2 19,4 3 12,9 4 9,8 5 7,7 6 6,4 d2 18,7 13,3 10,0 7,8 6,4 d3 18,9 12,7 9,9 7,7 6,3 1 Зависимость d от 𝑚 представлена в таблице 3 и на графике: таблица 3 1 1 𝑚 6 d 6,37 1 5 7,73 1 4 9,9 1 3 12,97 1 2 19 20 18 16 14 12 10 8 6 4 2 0 𝑦 = 0,385𝑥 0.166666667 0.2 0.25 0.333333333 0.5 Исходя из графика, получаем угловой коэффициент: 𝑘 = 0,385 Тогда найдем длину световой волны: 𝑟2 λ= 𝑘 где 𝑟 = 0,50 ± 0,02 мм – радиус отверстия 0,52 λ= = 0,649 мм = 649 нм 0,385 Расчет погрешности: 𝑁 ∆k 1 2 √ = ∗ ∑ (yi k 𝑦𝑏 – 𝑦𝑎 N − 2 − yср)2 𝑖=1 ∆k 1 2 √ = ∗ (0,782 + 0,772 + 0,292 + 0,462 + 0,862 ) = 0,0182 k 0,039 – 0,23 N − 2 ∆k = 0,0182 ∗ 0,385 = 0,007 2 2 2 2 ∂λ ∂λ 𝑟2 2r √ √ ∆λ = ( ∆k) + ( ∆r) = (− 2 ∆k) + ( ∆r) ∂k ∂r k k 2 2 0,00052 2 ∗ 0,0005 ∆λ = √(− ∗ 0,007) + ( ∗ 0,00002) = 5,33 ∗ 10−8 м = 53,3 нм 0,3852 0,385 Результат: λ = 649,0 ± 55,3 нм Вывод: В ходе работы я определил длину световой волны по картине дифракции на круглом отверстии на основе принципа Гюйгенса-Френеля, с помощью метода зон Френеля. Диапазон красного цвета спектра определяют длиной волны 620—740 нм, поэтому, значение 𝜆 = 649 ± 55,3 нм, полученное в результате выполнения лабораторной работы попадает под заданные значения диапазона. Погрешность составила около 8,5%, что является приемлемой погрешностью. Вызвана она в связи с неточностью измерений маленьких величин, а так же погрешностью при расчетах.