Тема: Квадратный корень из произведения и дроби

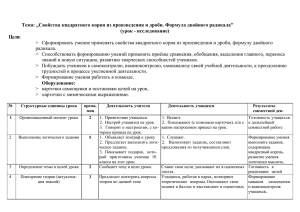
тема: Квадратный корень из произведения и дроби
Цели: Познакомить учащихся со свойствами квадратного корня
из произведения и дроби; закрепить навыки решения упражнений
Воспитывать внимание, аккуратность.
Развивать логическое мышление, культуру математического языка.
Ход урока.
I Устные упражнения (слайды)
Сформулируйте определение арифметического квадратного корня.
При каких значениях а выражения а
имеет смысл?
2. Какова область определения функции у = х ? Как расположен график этой функции в
координатной плоскости?
3. Выберите неверное равенство: а) 16  4; б) 0,4  0,2; в)7  25  2; г) 16  9  5
4.Вычислите 32  4 2
Варианты ответа:
а)7
б) 14;
в) 5
г) 17
5. При каких значениях х имеет смысл выражение
х х
а) При любых значениях;
б) таких значений нет; в) 0;
г) при х≤ 0;
д)при х≥0
6. Вычислите:
а) 0,49  2( 0,2 ) 2 ; б)(2 6 ) 2  1; в)(2  5 ) 2  4 5
II Историческая справка
Потребность в действиях возведения в степень и извлечения корня была вызвана
практической жизнью.
Так, наряду с задачей вычисления площади квадрата, с давних времён встречалась обратная
задача: какую длину должна иметь сторона квадрата, чтобы его площадь равнялась b? Знак корня
называют знаком радикала( от латинского слова radex-корень.B XVв.писали:R 2 12 вместо
12 .Немецкие математики обозначали квадратный корень точкой впереди числа или выражения. В
скорописи точки заменяли чёрточками позже перешедшими в символ
Вероятно из этих обозначений впоследствии и образовался знак v,близкий к современному символу
корня. Впервые запись корня, точно совпадающая с ныне принятой, встречается 1690 г.
III Изучение нового материала:
25
100
1 вариант : а) 81  4 ; б ) 25  9 ; в) 9  4;г
.
; д)
4
4
25
100
2 вариант : а) 81  4 ; б ) 25  4 ; в) 9  4 ; г )
; д)
4
4
Сравнить значения выражений. Какую гипотезу можно выдвинуть?
(Гипотеза – научное предположение, выдвигаемое для объяснения каких -нибудь явлений)
Теорема 1: Если а  0; в  0 , то ав  а  в (доказывает ученик)
Теорема 2:Если а  0; в >0, то
а

в
а
в
На доске учитель показывает решение примеров: а) 25  64 ; б )
IV Закрепление: №369(а,б,в), №370(а,в,д) №374(а,в), №376(а,в)
№374
36
; в) 32  16
144
а)  810  40  81  10  4  10  81  4  100  9  2  10  180
б ) 72  32  36  2  16  2  36  16  4  6  4  2  48
№376
а) 13 2  12 2  (13  12)(13  12)  25  5; в ) 313 2  312 2  (313  312)(313  312)  25
Повторить свойства.
V Самостоятельная работа с последующей самопроверкой на слайде:
1вариант
1.Найдите значения корня:
49
81
а) 9  36 ; ь) 16  900 ; в)
; г)
;
64
100
2.Найдите значения выражения:
а) 40  490 ; б ) 10  640 ; в ) 18  32
3.Вычислите:
а) 112  60 2 ; б ) 85 2  84 2
2вариант
1.Найдите значения корня:
25
81
а) 16  25; ь) 9  1600 ; в)
;г )
64
121
2.Найдите значения выражения:
а) 90  250 ; б ) 10  360 ; в) 8  32
3.Вычислите:
а) 8 2  15 2 ; б ) 612  60 2
Итог урока.
Рефлексия.
Что нового вы сегодня узнали на уроке?
Сформулируйте теорему о квадратном корне из произведения.
Сформулируйте теорему о квадратном корне из дроби
VI Домашнее здание: п.15 № 369(б,г,е), №370(б,г), №375