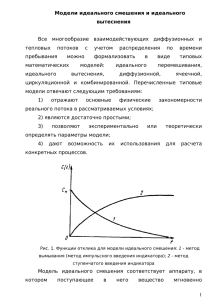
1. Основные понятия моделирования химико-технологических процессов. ... 1 2. Математическое описание химических реакций ........................................... 22 3. Процессы в потоке. Идеальные потоки. ......................................................... 39 4. Модели неидеальных потоков ......................................................................... 61 5. Оптимизация Теоретические вопросы. ........................................................... 84 1. Основные понятия моделирования химико-технологических процессов. Моделирование – старейший и важнейший метод науки и техники. Моделирование – один из важнейших методов, широко применяемых в современной науке, в первую очередь в ее прикладных областях. Моделирование позволяет ускорить технический прогресс, существенно сократить сроки освоения новых производств. В эпоху научно-технической революции особенно бурно развивается одно из новых направлений – математическое моделирование. Его развитие теснейшим образом связано с развитием информатики и вычислительной техники. Оригинал и модель – их сходство, по существу, и различие во всем ином. Два подхода к моделированию. Физическое (аналоговое, натурное) моделирование. Примеры аналоговых моделей: личность и портрет, скорость механического движения и отклонение стрелки амперметра, концентрация реагента и ток в электрической схеме, крыло самолета и деревянная модель в аэродинамической трубе. Суть моделирования заключается в следующем. Мы хотим исследовать поведение какоголибо объекта (оригинала) в тех или иных условиях. Но вместо оригинала исследуем поведение другого объекта – модели, а затем распространяем выводы такого исследования на оригинал – заключаем, как будет вести себя он. Пример 1.1. Прежде чем строить и запускать в воздух самолет, конструкторы подвешивают в аэродинамической трубе модель самолета и обдувают ее струей воздуха. Здесь моделью является не только малая геометрическая копия, подобная будущему оригиналу, но и воздух, движение которого моделирует движение самолета в атмосфере (поскольку движение относительно, то безразлично, летит ли аппарат в воздухе или воздух обтекает его). В примере 1.1 модели – некоторые материальные объекты, поведение которых «похоже» на поведение оригинала (аналогично ему). Необходимо только знать правило, по которому результаты эксперимента с моделью можно пересчитать на параметры, характеризующие оригинал (правило традукции). Такие модели обычно называют материальными. Но есть еще один класс моделей. Мы можем составить в уме схему (описание) нашего оригинала и затем, производя с этим описанием какие-либо преобразования, прийти к выводам, допускающим традукцию на оригинал. В таких случаях говорят о мысленных моделях. Здесь важнейший для практики вариант – тот, в котором описание дается на языке математики (математическая модель). В этом смысле любое математическое описание какого-либо процесса является его математической моделью. Чаще всего такая модель представляет собой уравнение или систему уравнений. При этом компьютер, решающий уравнения математической модели, ведет себя как материальная модель. В него можно вводить условия функционирования оригинала, и он покажет, как тот поведет себя в заданных условиях. Математическую модель, если она простая, можно исследовать и на бумаге, а иногда даже в уме. Главное, что отличает моделирование, это не просто вывод или решение уравнений, а исследование поведения объекта в различных условиях. Перенос данных с модели на объект: понятия подобия, масштабирования, традукции. При организации моделирования возникают вопросы: какие условия обеспечат традукцию и какова возможность распространения полученных данных на поведение оригинала? Эти условия различны в физическом и математическом моделировании. Традуктивность при физическом моделировании обеспечивается подобием оригинала и модели. Теория подобия – важнейшая часть теоретического фундамента науки о процессах и аппаратах химической технологии. Очень коротко можно сказать так: если два объекта (две системы) физически подобны друг другу, то процесс в каждом из этих объектов может быть описан набором безразмерных характеристик – чисел подобия, и в соответствующих точках обоих объектов числа подобия имеют равные значения. При этом те же самые числа играют роль критериев подобия – признаков, по которым можно установить, что подобие существует. А именно: если краевые и начальные условия процесса, выраженные через числа подобия, для одной системы – количественно такие же, как для другой, то процессы в обеих системах протекают подобным образом, системы все время остаются подобными друг другу. Набор необходимых критериев подобия определяют либо исходя из дифференциальных уравнений, описывающих процесс, либо основываясь на анализе размерностей. Метод подобия оказался высокоэффективным при моделировании гидромеханических процессов (течение жидкостей в каналах, фильтрация через пористые среды, движение морских и воздушных судов), процессов переноса тепла и вещества. Значительные трудности возникли при попытках моделировать на основе подобия химические процессы – процессы, основным содержанием которых являются химические превращения (реакции). Многолетний анализ этих трудностей показал, что во многих случаях они непреодолимы. Дело в том, что при изменении размеров объекта (масштабировании) разные критерии подобия могут предъявлять противоречащие друг другу требования к условиям проведения процесса в модели. Большинство химических процессов – это системы, подсистемами которых является целый ряд процессов, каждый из которых требует своих условий подобия. Очень часто реакция – сложная, и каждая из ее стадий по-своему зависит от концентраций и температуры; на ход реакции сильно влияют выделение (или поглощение) и перенос тепла, перенос вещества, движение потоков. Лишь в некоторых достаточно простых случаях удается сформулировать условия проведения процесса так, что масштабирование оказывается возможным. Чаще всего так бывает при проведении достаточно медленных реакций в аппаратах с мешалками. В большинстве остальных случаев добиться подобия при масштабировании не удается. Сложности, связанные с нарушением подобия при масштабировании, явились причиной того, что в середине прошлого века моделирование химических процессов находилось в глубоком кризисе. Выход из него нашелся – это математическое моделирование, где трудности, сопряженные с обеспечением подобия, снимаются. Здесь есть лишь одно главное требование: математическое описание моделируемой системы должно быть адекватным. Необходимо, чтобы все основные количественные закономерности достаточно точно воспроизводились в математической модели, остальное – уже дело вычислительных методов и вычислительной техники. А первое и самое главное – хорошо составленное математическое описание. Эффективность математического моделирования связана с замечательной особенностью многих систем – аналогией между ними. Аналогия – понятие, более широкое, чем подобие, о котором шла речь выше. Это определенное сходство между разными системами, причем физическое содержание этих систем может очень различаться. Важнейшее для практики свойство аналогичных систем – общность их математических описаний. Разные системы оказываются одинаково описанными, и их математическое моделирование осуществляется однообразно. В этом проявляется замечательная особенность математики – быть универсальной моделью, моделью любых систем. Аналоговое моделирование – моделирование, основанное на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых формально (одними и теми же математическими соотношениями, логическими и структурными схемами). Таким образом, аналогия не предполагает тождественности физической природы модели и прототипа, но требует, чтобы модель при некоторых условиях вела себя аналогично поведению оригинала (косвенное подобие). Аналогия основана на возможности моделирования явления (системы, процесса) одной природы явлениями (системами, процессами) совсем другой природы. Например, электромеханическая аналогия: колебания в механических системах можно моделировать колебаниями в электрических цепях. При этом модель (аналог) и оригинал (прототип) описываются одинаковыми математическими соотношениями, например дифференциальными уравнениями. Математическое моделирование. Эмпирическая и структурная модель, их сходство и различие. Мысленные, абстрактные модели. Алгебраические и дифференциальные уравнения и системы как модели физических объектов и процессов. Примеры математических моделей: Кошелек с деньгами и счет в банке. Истечение жидкостей, фильтрация жидкостей, ускорение материальных объектов, вязкое течение жидкостей, диффузия веществ в неподвижной среде, теплопроводность в твердых, жидких и газообразных средах, электропроводность. Линейные алгебраические уравнения и системы – самая простая и распространенная форма математической модели. Многие явления подчиняются идентичным, и часто линейным уравнениям алгебры – отсюда универсальность математических моделей. В структуре математических моделей разных процессов и явлений часто наблюдаются аналогии. Пример: равноускоренное одномерное перемещение и рост счета в банке с учетом процентов. Адекватность моделирования. Общее понятие о применимости результатов моделирования к объекту моделирования. Зависимость понятия адекватности от сферы применения модели. Пример: адекватность по цвету, по скорости, по массе, по форме, по срокам, по стоимости. Необходимость учета статистических характеристик измерений при оценке адекватности по количественным критериям. Сложности, связанные с нарушением подобия при масштабировании, явились причиной того, что в середине прошлого века моделирование химических процессов находилось в глубоком кризисе. Выход из него нашелся – это математическое моделирование, где трудности, сопряженные с обеспечением подобия, снимаются. Здесь есть лишь одно главное требование: математическое описание моделируемой системы должно быть адекватным. Необходимо, чтобы все основные количественные закономерности достаточно точно воспроизводились в математической модели, остальное – уже дело вычислительных методов и вычислительной техники. А первое и самое главное – хорошо составленное математическое описание. Эффективность математического моделирования связана с замечательной особенностью многих систем – аналогией между ними. Аналогия – понятие, более широкое, чем подобие, о котором шла речь выше. Это определенное сходство между разными системами, причем физическое содержание этих систем может очень различаться. Важнейшее для практики свойство аналогичных систем – общность их математических описаний. Разные системы оказываются одинаково описанными, и их математическое моделирование осуществляется однообразно. В этом проявляется замечательная особенность математики – быть универсальной моделью, моделью любых систем. Системный подход в моделировании. Система как совокупность связанных элементов. Связь не только механическая, но и любого иного типа, например, логическая. Состав элементов. Структура элементов. Статическая и динамическая система. Термодинамика и кинетика как примеры. Материальные и нематериальные элементы системы, например: стадии, мысли, слова, люди, уравнения, подсистемы. Определенные и неопределенные элементы, категории, классы. Система – совокупность каких-либо элементов, связанных, взаимодействующих друг с другом. Причем характер связей (взаимодействий) не менее важен для существования системы, чем сам набор элементов. Совокупность связей называют структурой системы. Пример 1.3. Комплект оборудования для работы химического производства, лежащий на складе, системой еще не является. После того как это оборудование соединили в соответствии со структурой процесса и оно заработало (связи актуализированы), тот же набор аппаратов, машин, коммуникаций стал системой. Элементами системы необязательно являются некие изделия, как в предыдущем примере, или вообще какие-то материальные предметы. Для нас важно рассматривать в качестве системы процесс, элементами которого являются более простые процессы (стадии). Так, химико-технологический процесс – система, которую можно мысленно разбить на стадии химического взаимодействия, процессов тепло- и массообмена, движения потоков и т.д. Ни понять смысл процесса, ни управлять им невозможно, не понимая, как эти стадии связаны друг с другом, как они влияют друг на друга. В иных задачах фигурируют системы, элементами которых могут быть математические выражения (например, система уравнений), мысли (например, система взглядов), слова (любой текст есть система) и т.д. Выделяют системы статические, не меняющиеся во времени (система уравнений, система слов в древнем тексте), и динамические. Типичная динамическая система «живет», все время взаимодействуя с окружающим миром и изменяясь. Чаще всего элементы данной системы сами являются системами. Такие элементы называют подсистемами. Пример 1.4. Один из важнейших элементов любого процесса биотехнологии – жизнедеятельность микроорганизмов, осуществляющих потребные нам реакции. Но жизнедеятельность любого организма сама по себе – сложнейший процесс, обладающий всеми чертами системы. Стало быть, она является подсистемой технологического процесса. Иерархия подсистем в природе и в модели как важнейшая особенность систем. Модели динамики потоков, химической кинетики, массопередачи, теплопередачи и т.п. Точечный объем – основа крупных математических моделей. Системный иерархический подход М.Г. Слинько в применении к моделям кинетики химических реакций, моделям химических реакторов. Уровни иерархии включают: молекулярный уровень, активный центр, пора, зерно катализатора, слой катализатора, рабочая зона аппарата, аппарат в целом, агрегат и т.д. В огромном числе систем существует иерархия подсистем: система состоит из подсистем первого уровня, каждая из них образована подсистемами второго уровня и т. д., причем количество уровней может быть очень велико. В таких случаях часто бывает удобно анализировать закономерности поведения системы, начиная с наинизшего уровня и переходя затем на более высокие. Так, для химико-технологического процесса используется иерархическая структура математической модели, предложенная М. Г. Слинько. Модель строится путем последовательного перехода в описании процесса с одного уровня на другой. 1. Молекулярный уровень – описание процессов, протекающих в масштабе порядка расстояния между молекулами. Их закономерности – это прежде всего закономерности химической кинетики. 2. Уровень малого объема, на котором объектом описания является, например, процесс на одном зерне катализатора или в пузырьке газа, поднимающемся в барботажном слое, и в обтекающей его жидкости, или на одном элементе насадки в насадочной колонне и т.д. Здесь закономерностей предыдущего уровня уже недостаточно, необходимо дополнить их закономерностями существенных в этом масштабе процессов тепло- и массопереноса. Анализ кинетических закономерностей в условиях одновременного протекания процессов переноса – предмет научного направления, называемого макрокинетикой 3. Уровень рабочей зоны аппарата (слой катализатора, барботажный слой, насадочный слой и т. д.), на котором необходимо учитывать эффекты, связанные с характером движения потока. В ряде случаев (например, при гомогенных реакциях) на этот уровень можно перейти прямо с первого. 4. Уровень аппарата, при переходе на который учитывают число, конфигурацию, взаимную связь и взаимное расположение рабочих зон. Например, аппарат может содержать несколько слоев катализатора, между которыми располагаются промежуточные теплообменники. 5. Уровень агрегата, где учитываются взаимные связи между аппаратами. Модель каждого высшего уровня содержит модели низших уровней и соотношения, описывающие переход с одного уровня на другой. Такой подход часто позволяет анализировать и моделировать процесс по частям, что существенно упрощает анализ; в то же время при этом не упускается из виду структура – характер связей уровней. Детерминированные и стохастические, континуальные и дискретные, внутренние и внешние, открытые и закрытые системы. Обобщенная форма детерминированной математической модели: Y=(X,Z). Явные и неявные по форме уравнения моделей Входные величины факторы (регулируемые и нерегулируемые, активные и пассивные, точечные и распределенные). Выходные величины отклики. И те, и другие могут быть непрерывными и дискретными. Положительные и отрицательные обратные связи в системе. Внешние связи системы. Определяя понятие «система», я уже говорил об исключительной важности связей между ее элементами. Для динамических систем не менее важны внешние связи – взаимодействия системы с окружающим ее миром. Внешние связи бывают двух основных классов: воздействия мира на систему – входы системы и воздействия системы на мир – ее выходы, результат функционирования системы. Особый случай – обратные связи: выход системы оказывает влияние на ее вход. Существуют положительные обратные связи, когда усиление выходного сигнала усиливает сигнал на входе, и отрицательные обратные связи, когда с усилением выходного сигнала входной ослабляется. Как правило, действие положительных обратных связей приводит к возбуждению системы, интенсификации ее деятельности; в неблагоприятных случаях это может привести к тому, что система «пойдет вразнос». Наоборот, отрицательные обратные связи стабилизируют состояние системы. Пример 1.5. Теплокровные животные, в том числе и люди, все время сохраняют почти постоянную температуру тела. Это обеспечивается рядом отрицательных обратных связей. Если окружающая температура понижается, включаются процессы, препятствующие охлаждению тела: например встает дыбом шерсть, снижая теплоотдачу; возникает дрожь, и при работе дрожащих мышц выделяется тепло (у человека шерсти нет, но механизм ее подъема еще сохранился – на коже появляются мурашки – напряжение 1.1. Моделирование и модели 15 микромышц, поднимавших волосы у наших предков). Если же температура слишком велика, усиливается выделение пота, его испарение забирает излишек тепла. Эта система обратных связей обеспечивает гомеостаз – свойство очень многих систем поддерживать свое состояние в таких пределах значений параметров, которые не угрожают существованию системы. Пример 1.6. Как происходит взрыв атомной бомбы? Влетевший в массу урана или плутония нейтрон (например, возникший при действии космических лучей) вызывает распад ядра с образованием более чем одного нейтрона. Это положительная обратная связь. Часть нейтронов вылетает наружу – это отрицательная обратная связь. Если масса металла меньше критической, превалируют отрицательные связи и система стабильна. Если критическая масса превзойдена, система идет вразнос – происходит взрыв. О классификации входов системы. Входные воздействия (чаще всего будем называть их факторами, влияющими на систему) можно подразделить на две основные группы. Первая – контролируемые факторы. Это те воздействия, величины которых мы знаем или по крайней мере можем узнать, когда это потребуется. В свою очередь, эта группа факторов подразделяется на регулируемые и нерегулируемые. Регулируемые (управляющие) факторы те, значения которых мы сознательно меняем (регулируем) с целью управлять процессом – улучшать его показатели. Значения нерегулируемых факторов мы можем знать, но не изменяем, либо оставляя постоянными, либо мирясь с тем, что они как-то меняются помимо нашей воли, и лишь приспосабливаясь к этим изменениям. Существуют, по крайней мере, три причины, по которым фактор может оказаться нерегулируемым: 1) его изменение практически невозможно – например, это размер установленного аппарата; 2) его можно изменить, но это слишком дорого – например, это состав поступающего сырья; 3) он слабо влияет на процесс и его нецелесообразно регулировать – например, это содержание аргона в воздухе, поступающем в топку. Пример 1.7. В большинстве технологических процессов температура и влажность окружающего воздуха не регулируются. Однако при изготовлении синтетических тканей эти факторы заметно влияют на качество продукции и их необходимо регулировать (кондиционировать воздух). Кроме контролируемых факторов в любом процессе наличествует бесчисленное множество факторов неконтролируемых, причем мы можем даже не знать о их существовании. Почему так может быть? Во-первых, мы иногда не знаем, что данный фактор заметно влияет на наш процесс. В таких случаях приходится говорить, что процесс недостаточно изучен, и зачастую без дальнейших исследований его нельзя реализовать. Но есть и иная причина, действующая даже тогда, когда процесс изучен хорошо. В любом реальном случае имеется огромное, практически бесконечное число очень слабых воздействий. Каждое из них нет смысла контролировать, потому что оно слабое. Все – нельзя потому, что их слишком много. В то же время совокупное действие этого множества уже не мало, оно заметно влияет на функционирование системы. Это влияние обладает одной важной особенностью. Не контролируя входы, мы не можем знать, каково оно в данный момент и каким окажется впоследствии. Поэтому воздействие неконтролируемых факторов носит случайный характер. При измерениях оно выражается в случайных погрешностях, в эксперименте – в случайных ошибках, при протекании любого процесса – в случайных возмущениях. Дискретные величины принимают определенные конечные значения. Непрерывные величины: количественные данные, принимающие значения на непрерывной шкале значений. Примеры непрерывных переменных: (температура, давление, скорость, ускорение, сила тока, концентрация и тд) Шум – флуктуации, погрешности, ошибки, возмущения. Упрощенная форма: Y=F(X)+(Z) – зависимость (математическая детерминированная модель) плюс шум. Случайные неконтролируемые воздействия могут не только приходить извне, но и возникать внутри системы. Однако чаще всего нет смысла подробно разбираться, откуда они исходят: случайные колебания, случайные отклонения в процессе целесообразно рассматривать как нечто единое. Часто это единое обозначают термином шум. На систему воздействуют изменяющиеся входные факторы, и система отвечает на их изменения изменением выходных величин (откликов системы на воздействия). Для сокращения записи используем понятие «вектор»: вектор – упорядоченная последовательность величин (например, последовательность значений всех факторов или всех выходов системы в данный момент, записанная в строку или в столбец). Векторы (а в дальнейшем и матрицы) будем обозначать полужирными буквами. Так, вектор факторов Х – это записанные по порядку значения х1 , х2 , х3 , …, хn , где n – число факторов. Тогда математическое описание для любого из выходов системы имеет наиболее общий вид где i – номер выходной величины; X – вектор контролируемых факторов; Z – вектор неконтролируемых факторов. Но пользоваться уравнением (1.8) или хотя бы установить его вид невозможно. Ввиду неконтролируемости Z нет возможности даже составить список аргументов функции. В большинстве случаев удается упрощенно записать эту функцию в виде разбив ее на два слагаемых: зависимость Fi (X) и шум Ψi (Z). Тогда задача получения математического описания разбивается на две: установить вид каждой из зависимостей Fi и оценить шум Ψi . Это разные задачи. Для Fi необходимо получить аналитическое выражение, а для Ψi – случайной величины – лишь оценку, указывающую, в каких пределах и с какой вероятностью может колебаться шум. Чаще всего математической моделью называют именно набор функций F : полагая, что это и есть «истинная» зависимость, а наличие шума лишь искажает ее. Структурный и эмпирический подходы, их связь, достоинства и недостатки. Параметры и их определение. Эксперимент и его планирование. Существует два подхода к описанию системы. Первый подход можно назвать структурным. Суть его заключается в следующем. Для создания математической модели системы прежде всего исследуем ее структуру – составляющие систему элементы и характер их взаимодействия. Применительно к технологическому процессу это означает расшифровку его механизма. В результате получается схема процесса – его мысленная модель. Для химико-технологического процесса мысленная модель на физическом языке содержит прежде всего представления о механизмах реакций, характере движения потоков, процессах переноса тепла и вещества и о взаимном влиянии химизма, гидравлики, тепло- и массопереноса. Записав эту схему на языке математики, получаем некую систему уравнений, описывающих процесс. Обычно на этом этапе уравнения получаются в общем виде – в них входят некоторые пока неизвестные коэффициенты (константы скоростей реакций, коэффициенты тепло- и массоотдачи и др.). Эти коэффициенты называют параметрами модели. Для определения параметров ставится эксперимент (на моделях, а иногда и на оригинале, если таковой имеется), результаты которого позволяют получить математическое описание в полном виде, со всеми коэффициентами. Второй подход к описанию системы – эмпирический. Другое его распространенное название – метод черного ящика. Предположим, что структура интересующей нас системы скрыта от нас (как бы заключена в «черный ящик»). Это не означает, что системой нельзя управлять. Как бы черен ни был ящик, у системы есть важные контакты, которыми можно воспользоваться для ее анализа и управления ею. Эти контакты – входы и выходы системы. Будем изменять значения входов и определять, как при этом изменяется отклик. Каждый такой акт – изменение входов и определение отклика – есть не что иное, как эксперимент. Проведя определенное число экспериментов, опишем их результаты эмпирическим уравнением или системой эмпирических уравнений. Эти уравнения и будут математической моделью, которой можно воспользоваться для моделирования данной системы. Любое эмпирическое описание отражает, хотя и в неявной форме, механизм процесса. Иногда это отражение оказывается настолько характерным и точным, что анализ эмпирического уравнения прямо приводит к раскрытию механизма. Эмпирическое уравнение обязательно содержит в себе структуру, но только структуру нерасшифрованную. Поэтому четкое противопоставление обоих подходов носит характер методический, а не прикладной. В практических задачах наблюдаются самые разнообразные соотношения между уровнями структурности и эмпиричности применяемых методов. Главное достоинство эмпирического подхода – простота. Особенно существенно оно сказывается при изучении очень сложных процессов. Главная его слабость – малая надежность экстраполяции. В пределах изменения переменных, изученных в опытах, предсказание поведения процесса (интерполяция) обычно может проводиться достаточно точно. Но закон изменения функций отклика за изученными пределами нам неизвестен и можно допустить серьезную ошибку, полагая, что процесс по-прежнему обязательно будет подчиняться выведенным эмпирическим уравнениям. В практике моделирования одним из важнейших случаев экстраполяции является масштабирование: предсказание того, как изменятся параметры процесса при переходе от малой модели к большому оригиналу. На основе эмпирических зависимостей эта задача, как правило, решается гораздо хуже, чем при структурном подходе. Главное достоинство данных, полученных на основе структурного подхода, – их большая прогностическая мощность. Зная достаточно полно механизм какого-либо процесса, можно с большой степенью достоверности предсказывать ее поведение в самых разнообразных условиях. Поэтому, как гласит известный афоризм, «нет ничего практичнее хорошей теории». Слабое место подхода – трудность создания хорошей теории сложных процессов. Если выделить лишь один элемент химико-технологического процесса – его гидродинамику, то приходится считаться с отсутствием на сегодня сколько-нибудь удовлетворительной общей теории турбулентности. Далее, современная химия охватывает сотни тысяч веществ, и если задаться целью всерьез расшифровать механизмы реакций получения всех этих веществ, то вряд ли удастся достичь этой цели в обозримый срок. Подобные затруднения встречаются на каждом шагу. Понятно, что рассчитать эмпирические уравнения, как правило, бывает проще, чем получить информацию, достаточную для расшифровки механизма процесса. Матописание при структурном подходе (балансы, аддитивность): субстанция, контур, база. Пять статей баланса: Вход, Уход, Источник, Сток, Накопление. Стационарность. В любом сколько-нибудь серьезном случае все описание объекта, как бы хорошо он ни был изучен, нельзя построить на чисто теоретической основе. Какие-то параметры всегда придется определять из опытов и опытным же путем проверять адекватность модели – достаточную точность ее соответствия оригиналу. Большинство математических моделей химико-технологических процессов основываются на уравнениях баланса. Эти уравнения устанавливают соотношения между прибылью и убылью различных субстанций в рассматриваемой системе. Аддитивность – свойство балансовых уравнений, означающее, что их можно было складывать и вычитать. Все балансовые уравнения должны обладать аддитивностью. Для составления баланса необходимо выбрать три вещи: 1. Субстанция. Субстанцией может быть, например, вещество. Тогда имеем уравнение материального баланса. Если субстанция – тепло, то получим уравнение теплового баланса. Обратим внимание вот на что: закона сохранения тепла не существует, оно может возникать (из других форм энергии), может исчезнуть, перейдя в другие формы, но это не препятствует определению баланса. Что же касается материального баланса, то здесь встречаются два основных случая. Один – когда в качестве субстанции выбрана вся совокупность веществ, проходящих через систему. В этом случае действует закон сохранения массы, что учитывается при записи уравнения. Другой случай: субстанция – одно из веществ. Для конкретного вещества нет закона сохранения. Оно может возникать как продукт реакции, может исчезать, превращаясь в другие вещества. 2. Контур, ограничивающий в пространстве систему или ее часть (подсистему), для которой будет составляться баланс. Контур может охватывать рассматриваемый нами аппарат либо совокупность нескольких связанных между собой аппаратов, либо только одну рабочую зону аппарата. Каждый раз получим иное уравнение баланса. Особый случай – когда контур охватывает бесконечно малый элементарный объем. Часто такой подход является самым плодотворным. Заметим, что при этом, вследствие бесконечной малости объема, математическая модель получится в виде дифференциального уравнения или системы дифференциальных уравнений. И еще один особый вариант – когда контур «разорван» в пространстве (многосвязен). Так, дальше при рассмотрении задач стехиометрического анализа в некоторых случаях контур «охватывает» все молекулы данного сорта, не включая иные молекулы, при этом такая особенность контура может быть специально не оговорена, приходится о ней догадываться. 3. Интервал времени, за который составляется баланс. Здесь тоже возможен ряд вариантов. В качестве интервала можно принять единицу времени: составить баланс за секунду, за год. Можно рассмотреть баланс за бесконечно малый интервал времени dt. При этом, как и в случае бесконечно малого элементарного объема, упрощаются многие закономерности, и также получается математическая модель в форме дифференциальных уравнений. Возможен и такой выбор: наш интервал – время операции, без явного соотнесения его с единицей времени. Например, мы вправе рассматривать баланс химического синтеза за полное время синтеза, сколько бы оно не длилось, или, скажем, в периодическом процессе отдельно составить баланс за время загрузки, отдельно – за время протекания реакции и т.д. Часто баланс относят к базе расчета. Например, при рассмотрении процесса синтеза аммиака в качестве базы расчета можно принять получение 1000 т аммиака или переработку 1 000 000 м3 азотоводородной смеси. Несложно установить связь между понятиями «интервал времени» и «база расчета»: интервалом окажется время, за которое получается 1000 т продукта, или то, за которое перерабатывается 1 млн м3 исходной смеси. Но если выбрана база расчета, пересчитывать ее на время не нужно, и баланс относят непосредственно к этой базе. После того как выбор произведен, можно приступать к составлению уравнений баланса. Уравнения эти содержат пять составных частей (пять статей баланса). Четыре первых схематически показаны на рис. 1.1. Сокращенно каждая статья обозначена первой буквой. Овал обозначает контур. В (вход) – количество субстанции, входящей снаружи в систему на протяжении выбранного интервала времени; У (уход) – количество субстанции, уходящей за тот же интервал наружу; И (источник) – количество субстанции, возникающей (образующейся) за интервал времени внутри системы; С (сток) – количество субстанции, исчезающей (расходуемой) внутри системы за тот же интервал. Пятая статья баланса – накопление Н – на схеме не обозначена. Ее можно определить так. В каждый момент внутри системы находится какое-то количество субстанции. Накопление – это его приращение за интервал времени, разность между количеством субстанции в системе к концу интервала и количеством, которое было в начале. Из такого определения следует, что накопление может быть положительным (количество субстанции увеличилось), отрицательным (ее количество уменьшилось) и равным нулю (к концу интервала оно такое же, как было в начале). В стационарном процессе накопление равно нулю. Стационарный процесс - процесс параметры которого (во всяком случае те параметры, которые важны в рамках данного рассмотрения) не меняются во времени. Напишем общий вид уравнения баланса: В + И – (У + С) = Н. (1.11) В случае стационарного процесса Н = 0 и уравнение получает вид В + И – (У + С) = 0. (1.12) Соблюдение уравнения (1.12) необязательно означает, что процесс стационарен. Вообще, часто, в зависимости от особенностей баланса, можно заранее сказать, что некоторые статьи равны нулю. Так, если действует закон сохранения, то, очевидно, И = 0; С = 0. Математическое описание химических процессов в большинстве случаев состоит из уравнений баланса – прежде всего материального и теплового. Значения отдельных статей баланса обусловлены закономерностями процесса. Вход вещества определяется расходом входящего потока и концентрацией данного вещества в нем; вход тепла зависит от энтальпии входящей жидкости, ее расхода и от передачи тепла снаружи через стенки. Источники и стоки тепла и вещества пропорциональны скоростям реакций в рабочей зоне и т.д. Какими уравнениями будет описан процесс – конечными, обычными дифференциальными или дифференциальными в частных производных – зависит от выбора контура и интервала времени, а те в свою очередь – от особенностей потоков в рабочей зоне и стационарности или нестационарности процесса. Адекватность, параметрическая чувствительность, однозначность оценок, однозначность структурной и параметрической идентификации, непрерывные и корпускулярные среды. Ни одна модель в принципе не способна отразить оригинал полностью и всесторонне. Это положение одинаково верно как для материальных, так и для мысленных моделей. Более того, часто оказывается, что на практике целесообразнее пользоваться менее «совершенной» моделью, отражающей только отдельные черты оригинала и совсем не похожей на оригинал с других точек зрения. Параметры модели. Чаще всего простота или сложность математической модели связаны с тем, сколько в нее входит параметров – коэффициентов, учитывающих те или иные особенности объекта. Значения параметров характеризуют свойства данного конкретного объекта, отличающие его от других объектов того же класса. Чем больше параметров входит в модель, тем подробнее удается охарактеризовать его и тем точнее описать. На одном полюсе здесь выступают предельно идеализированные модели, такие, как идеальный газ, абсолютно упругое тело и др. Уравнения при этом либо вообще не содержат параметров, включая лишь универсальные константы (идеальный газ), либо их число минимальное (модуль упругости в законе Гука). На другом полюсе — сложные многопараметрические модели, учитывающие много конкретных свойств. Так как мы всегда хотим иметь максимально точное описание объекта, с этой точки зрения сложные модели обладают несомненными преимуществами. Но у сложных моделей есть и недостатки. Прежде всего такую модель трудно обрабатывать. Если данная модель входит как составная часть в сложные модели более высоких иерархических уровней, то в конце концов может получиться такое громоздкое описание, что его не удастся обсчитать. Хотя такая наглядность, возможность составить общее представление о характере зависимости не обязательно нужна при моделировании, но обычно она заметно облегчает анализ. Еще одна трудность, связанная с применением многопараметрических моделей, — это чувствительность к ошибкам опытов. Чем больше параметров, тем более точный эксперимент требуется, чтобы достаточно хорошо оценить эти параметры. Если модель построена на основе структурного подхода, а эксперимент не очень точен, то возникает специфическая опасность потери физического смысла: можно получить неверные значения параметров, хотя модель в целом будет давать приемлемое совпадение с опытными данными. Это происходит потому, что ошибки в значениях разных параметров взаимно компенсируются. Модель остается пригодной для количественного описания объекта (в достаточно узких пределах), но физический смысл искажается — мы получаем превратное представление о величинах эффектов, связанных с параметрами. В конце концов физический смысл теряется и параметры модели получают смысл подгоночных параметров, назначение которых — лишь привести в соответствие данные и модель. Уравнение становится эмпирическим, о чем исследователь может не знать. Основной вывод из сказанного: если необходима высокая точность описания, следует применять многопараметрические модели, но при этом эксперимент должен отличаться высокой точностью и большим объемом. Если же требования не столь велики, чаще всего целесообразно использовать простейшую из моделей, обеспечивающих нужную точность. Впрочем, в конкретных случаях требуется конкретное рассмотрение. Бывает и так, что из двух возможных моделей мы выберем несколько более сложную, зато более ясную физически. Дать непогрешимый рецепт на все случаи жизни невозможно. Модели сплошных сред и квазигомогенные модели. Разделы физики (и примыкающие разделы химии), исходящие из модели вещества как среды, параметры которой меняются непрерывно, объединяют названием физика сплошных сред. Предмет каждого из этих разделов в принципе можно описать и на основе молекулярных представлений. Но описание при этом получается неизмеримо более сложным. Модель сплошной среды удобна для использования такого мощного математического аппарата, как дифференциальное и интегральное исчисления. Даже в случаях, когда наряду с моделью сплошной среды существует хорошо разработанная молекулярная модель, вторая не вытесняет, а дополняет первую (сравните термодинамику и статистическую физику). Удобства, получаемые при использовании модели сплошной среды, столь велики, что таким же образом часто рассматривают объекты, состоящие не из молекул, а из гораздо более крупных частиц. Мы описываем, например, течение эмульсии в трубе как течение однородной жидкости, характеризующейся некоей эффективной вязкостью, которая сложным образом зависит от свойств и соотношения фаз, а также от размеров и формы частиц. Зерно катализатора (сложного конгломерата, по порам которого диффундирует вещество, реагирующее на стенках пор) часто описывается как некоторая однородная среда. Подобные схемы, упрощенно представляющие многофазную систему как однородную, называют квазигомогенными моделями. Лимитирующая стадия, квазистационарное и квазиравновесное приближение, сосредоточенные и распределенные параметры, конечные и дифференциальные уравнения, прямые и обратные задачи, проектные и поверочные расчеты. Лимитирующие стадии. Многие интересующие нас процессы многостадийны, т. е. распадаются на ряд стадий (этапов, путей). Описание и анализ многостадийного процесса удается существенно упростить в тех случаях, когда одна из стадий лимитирует процесс. То, какая именно стадия может лимитировать процесс, определяется, с одной стороны, соотношением скоростей (или производительностей, мощностей) разных стадий, а с другой – их взаимным расположением. Если стадии последовательны, то лимитирует самая медленная (наименее производительная), если стадии параллельны, то лимитирует самая производительная. Наконец, случается, что ни медленная, ни быстрая стадия не могут лимитировать процесс. Это бывает, когда, казалось бы, нелимитирующая стадия влияет на протекание той стадии, которая должна была бы лимитировать. Стационарные и нестационарные процессы. Простейшим для анализа случаем является стационарный процесс. Его параметры (во всяком случае те параметры, которые важны в рамках данного рассмотрения) не меняются во времени, поэтому время как переменная исчезает из описания. В частности, в соответствующих уравнениях отсутствуют производные по времени. По сути своей стационарные процессы непрерывны, а значит, они обязательно проходят в открытых системах, т. е. системах, обменивающихся веществом с окружающей средой. Именно этот обмен – ввод исходных материалов и вывод продуктов – и поддерживает непрерывность. В аппарате, в котором идет непрерывный процесс, обязательно движется поток. Нестационарные процессы характеризуются изменением параметров во времени. Нестационарными являются все периодические процессы. Кроме того, нестационарно может работать и аппарат непрерывного действия. Это происходит во время переходных процессов, заключающихся в переходе от одного стационарного режима к другому. Переходные процессы возникают при пуске, остановке, переналадке режима, а также вследствие случайных возмущений – колебаний процесса под воздействием неконтролируемых факторов. Нестационарный процесс может протекать как в замкнутой системе, не обменивающейся веществом с окружающей средой (например, в автоклаве), так и в открытой системе (периодическая ректификация, переходный процесс в аппарате непрерывного действия и т. д.). В некоторых случаях один и тот же процесс можно описать и как стационарный, и как нестационарный – в зависимости от системы переменных, в которой проводится описание. Так, процесс в потоке может рассматриваться как стационарный при описании его в координатах, неподвижных относительно аппарата: в данной точке аппарата концентрации и температура не меняются во времени. Но если тот же процесс описать в координатах, движущихся с потоком, описание окажется нестационарным: по мере движения в потоке концентрации меняются вследствие протекания реакции. Объекты с сосредоточенными и распределенными параметрами. Эти понятия являются пространственными аналогами стационарности и нестационарности. Если объект таков, что можно пренебречь различием параметров процесса в разных точках и считать, что все они (концентрации, температура и др.) полностью выровнены по объему, то это объект с сосредоточенными параметрами. В описании такого объекта отсутствуют производные по координатам (все они равны нулю), что сильно упрощает модель. В некотором смысле объект с сосредоточенными параметрами можно рассматривать как точку, в которой происходит процесс, поскольку во всех других точках все происходит точно так же. Описание в этом случае будет наиболее простым. Если параметры процесса существенно меняются от точки к точке, то это объект с распределенными параметрами. В его описании возникают производные, по крайней мере, по одной координате, а возможно, и по всем трем. Поэтому описание и анализ здесь сложнее, чем в случае сосредоточенных параметров. Конечные и дифференциальные уравнения. Математическая модель может содержать как конечные уравнения, не содержащие операторов дифференцирования, так и дифференциальные уравнения. Конечные уравнения возникают, например, при описании стационарных процессов в объектах с сосредоточенными параметрами. Они могут быть алгебраическими либо трансцендентными. В последние входят трансцендентные функции от неизвестных. Так, трансцендентны уравнения, содержащие аррениусовы члены (учитывающие влияние температуры на скорости реакций). Обыкновенные дифференциальные уравнения содержат функции лишь одной независимой переменной. Линейные уравнения (и их системы) могут быть решены аналитически. Нелинейные уравнения чаще всего целесообразно решать на компьютере. Дифференциальные уравнения в частных производных появляются в задачах, где имеется более одной независимой переменной. Решение их чаще всего представляет собой сложную математическую задачу и обычно требует применения компьютера. Задачи Коши и краевые задачи. При численном решении систем обыкновенных дифференциальных уравнений встречаются два основных случая, связанные с характером задания начальных условий. Первый – все начальные условия заданы при одном и том же значении независимой переменной. Это задача Коши. Например, протекание сложной реакции, в которой участвуют в качестве реагентов и продуктов n веществ, описано п дифференциальными уравнениями; начальные условия заданы в виде п начальных концентраций веществ в момент времени t= 0. Численное решение задач Коши сводится к той или иной расчетной схеме, в которой осуществляется расчет зависимых переменных при движении от начального до конечного значения независимой переменной. Значительно сложнее расчет в том случае, когда начальные (точнее, краевые) условия заданы при различных значениях независимой переменной. Здесь мы имеем дело с краевой задачей. Краевые задачи часто возникают, например, при описании процессов с противотоком фаз. Процедуры решения для краевых задач, как правило, значительно сложнее, чем для задач Коши. Теперь рассмотрим некоторые задачи, которые различаются тем, относительно каких величин, входящих в математическую модель, следует разрешать уравнения. Прямые и обратные задачи. Обратимся к уравнению (1.10). Более подробно это уравнение (общий вид уравнения математической модели) может быть представлен как yi = Fi (X,B), (1.20) где B = (b0 , b1 ,…., bp ) – вектор параметров. Запись (1.20) отражает тот факт, что в модель обязательно входят параметры. Возможны два основных класса задач, связанных с уравнениями вида (1.20). Задача первого класса. Нам заданы X, В. В этих условиях следует определить yi . Это прямая задача. В такой формулировке она сводится к расчету функции, заданной в явной форме. Если рассмотреть переменные Х, то решение данной задачи дает изменение величины y, или распределение y в пространстве факторов. Задача второго класса. Нам задано распределение (как правило, в виде совокупности экспериментальных данных) y в пространстве факторов X и известен общий вид функции (1.20). Требуется определить параметры b0 , ..., bр . Это обратная задача. Поверка. Проектные и поверочные расчеты. Проектным расчетом называют такой, цель которого состоит в определении требуемых размеров аппарата, при которых могут быть достигнуты заданные показатели. Поверочным расчетом называют такой, в котором мы задаемся размерами аппарата и находим, какие показатели могут быть при этом достигнуты. (то, что имеем) !!! Во многих случаях целесообразно свести проектный расчет к совокупности поверочных: задаться рядом типоразмеров аппаратов, для каждого из них рассчитать достижимые показатели, после чего выбрать наилучший размер. 2. Математическое описание химических реакций Статика и динамика реагирующих химических систем (состав (состояние), равновесие, кинетика). Стехиометрия как описание состава (не структуры). Стехиоме́трия— система законов, правил и терминов, обосновывающих расчёты состава веществ и количественных соотношений между массами (объёмами для газов) веществ в химических реакциях. Химическая формула как объект алгебры. Реагент, продукт, интермедиат – реактант, вещество. Уравнения реакции (стадии) как объекты алгебры. Линейная зависимость стадий в задачах химии. С + О2 = СО2 , (3.1) С + СО2 = 2СО, (3.2) 2С + О2 = 2СО. (3.3) Стадия (3.3) может быть представлена как сумма (3.1) и (3.2): если мы формально сложим первое уравнение со вторым и приведем подобные, т.е. взаимно уничтожим символы СО2 в левой и правой частях, то получим уравнение (3.3). То есть, третья строка является линейной комбинацией первых двух (сумма – простейший, хотя не единственный, случай линейных комбинаций). Стехиометрическое уравнение реакции имеет ясный количественный смысл. Поэтому обращение с формулами веществ как с величинами корректно. Это важное свойство стехиометрических уравнений назовем алгебраичностью. Линейная зависимость или независимость ничего не говорит о реальном механизме реакции. В одних случаях линейно независимая схема отвечает действительному ходу процесса, в других – процесс содержит и линейно зависимые стадии. Линейная независимость стадий важна при решении задач химического равновесия в сложных (многостадийных) реакциях. Здесь линейно независимой системе стадий соответствует достаточный для описания и расчета набор констант равновесия. А для любой линейно зависимой стадии константа может быть получена как функция констант этого набора. Например, для реакций (3.1) – (3.3) имеем К3 = К1 · К2 . Механизм как частный случай стехиометрии. Стехиометрическая матрица (однородные уравнения). Нумерация: m реакций, n реактантов. АхФ=У. Ранг А и число ЛН стадий и реактантов. Вернемся к реакциям (3.1) – (3.3). Сейчас каждое из этих уравнений рассматривается как стадия единой сложной реакции. В соответствии с алгебраичностью уравнений мы вправе перенести все члены уравнений в одну сторону: – С – О2 + СО2 = 0, – С – СО2 + 2СО = 0, (3.4) – 2С – О2 + 2СО =0. В системе (3.4) знаки выбраны так: если какое-то вещество J на данной стадии расходуется, его стехиометрический коэффициент aJ < 0; если J образуется, aJ > 0; если J не участвует в стехиометрии данной стадии, то aJ = 0. Это правило знаков будем широко использовать в дальнейшем изложении. Система уравнений (3.4) – это система однородных уравнений 1-й степени (однородные уравнения – такие, у которых свободные члены равны нулю). Такая система может быть полностью охарактеризована матрицей коэффициентов: Здесь n – общее число веществ; m – число стадий реакции; aij – стехиометрический коэффициент j-го вещества в i-й стадии с учетом правила знаков. Матрицу a называют стехиометрической. Матрица размера m × n – прямоугольная таблица (m строк и n столбцов), составленная из чисел или алгебраических выражений aij, называемых элементами матрицы. Квадратная матрица n × n – это матрица, в которой число строк равно числу столбцов. Для нее число n называют порядком матрицы. Подматрица матрицы – это такая матрица, которая получается из данной путем вычеркивания любого числа столбцов и любого числа строк. Определитель (детерминант) квадратной матрицы, элементы которой числа, – это число, получаемое из элементов по определенному правилу, которое здесь не приводится из-за громоздкости. Если определитель равен нулю, то матрицу называют вырожденной (особенной), если не равен, – то невырожденной (неособенной). Ранг матрицы. Рассмотрим все возможные квадратные подматрицы порядка l некоторой матрицы а размера m × n (рассматриваются любые целые положительные l, удовлетворяющие условию l ≤ m и l ≤ n). Некоторые из этих подматриц окажутся вырожденными, другие – невырожденными. Найдем наибольший порядок l макс, для которого существует хотя бы одна невырожденная подматрица. Этот порядок называют рангом матрицы а и обозначают r g a: r g a=l макс. (3.7) Ранг матрицы и число линейно независимых строк (столбцов). Если m ≤n и r g a =m, то все m строк матрицы линейно независимы. Если r g a < m, то среди строк имеется (m – r g a) линейно зависимых. Точно так же если n ≤m и r g a =n, то линейно независимы все столбцы, а если r g a < n, то в матрице имеются линейно зависимые столбцы. В частности, отсюда следует, что для того, чтобы система реакций была линейно независимой, необходимо, чтобы число строк (стадий) не превышало числа столбцов (веществ). Более подробное рассмотрение показывает, что необходимое условие линейной независимости стадий еще жестче: m < n. (3.8) В линейно независимой системе число реакций всегда меньше числа веществ, участвующих в ней как исходные (реагенты) и как продукты. Атомная матрица Н: n реактантов, l атомов (квазиатомов). Ф=НхЗ. Стехиометрическое правило Гиббса RkA n-RkH. Удобным инструментом при анализе стехиометрии является атомная матрица Строки этой матрицы соответствуют веществам, участвующим в реакции, а столбцы – атомам, из которых состоят эти вещества. Элемент hpq матрицы – количество атомов данного сорта q в молекуле (или формульной единице) вещества Ap ; n – общее число веществ; s – количество сортов атомов, составляющих эти вещества. Так, для реакции (3.1) – (3.3), если пронумеровать вещества в порядке С, О2 , СО, СО2 , а атомы в порядке С, О, то Важная особенность атомных матриц – возможность в ряде случаев вводить в нее в качестве столбцов квазиатомы. Если какая-либо группа атомов переходит из одних веществ в другие, нигде не изменяясь количественно, то такая группа может рассматриваться как «атом», точнее квазиатом. Преобразованием стехиометрической и атомной матриц можно получить правило Гиббса: r g a ≤n – r g h, где n – число веществ–участников реакции. Здесь знак «<» может быть только в том маловероятном случае, когда в записи системы уравнений пропущена какая-то линейно независимая стадия. В обычном случае правило Гиббса – это равенство: r g a=n – r g h. (3.17) Например, для реакций (3.1) – (3.3) n = 4, ранг матрицы (3.10) равен 2; значит, r g a= 4 – 2 = 2 и две из стадий реакции линейно независимы. Для реакций (3.11) n= 6, r g h= 3; отсюда r g a= 6 – 3 =3 и все три стадии линейно независимы. Можно сформулировать два правила, позволяющих в неслишком трудных случаях находить линейно независимые стадии сложных реакций, не прибегая к формальному анализу. Процедура заключается в последовательном вычеркивании независимых стадий. Правило 1. Если стехиометрический коэффициент какого-то вещества отличен от нуля только в одной из стадий, эта стадия независима и ее можно вычеркнуть. Правило 2. После такого вычеркивания для оставшихся стадий продолжает действовать правило 1. Вычеркивание продолжается либо до тех пор, пока не останется лишь одна стадия (она, разумеется, будет независима), либо пока для немногих оставшихся стадий не удастся установить линейную зависимость. Простая и сложная реакция. Химическая переменная =gi/ai – обозначение глубины протекания стадии (знак плюс по продукту). Рассмотрим формально одностадийную реакцию: а1 А1 + а2 А2 + … +аn Аn = 0. (3.18) Формально простой (формально одностадийной) будем называть реакцию, стехиометрическое уравнение которой можно записать «в одну строчку», в виде (3.18). На деле механизм реакции может оказаться сложным, она может проходить через ряд промежуточных стадий, но запись (3.18) означает, что в нашем рассмотрении их продукты не обнаруживаются (обычно из-за большой скорости промежуточных стадий). При более прецизионном исследовании та же реакция может предстать как сложная, однако сейчас ее можно считать простой. Часто понятие «формально простая» еще расширяют, распространяя его и на обратимые реакции; но в данном случае это не важно, потому что любая обратная реакция линейно зависит от прямой. При этом (3.18) может быть и той реакцией, которая нас интересует, и одной из стадий более сложной реакции. Обратим внимание на следующее. Уравнение (3.18) означает, что превращающиеся количества веществ пропорциональны их стехиометрическим коэффициентам. Поэтому для рассматриваемой одностадийной реакции (или стадии сложной реакции) отношение количества превратившегося вещества ∆g [моль] к стехиометрическому коэффициенту – одно и то же для всех веществ, следует лишь учитывать знаки ∆g и а: ∆g1 / a1 = ∆g2 / a2 = … = ∆gn / an = ζ. (3.19) Величину ζ будем называть химической переменной. Если сложная реакция состоит из нескольких стадий, то протекание каждой из стадий характеризуется своей химической переменной, как правило, иной, чем переменные других стадий. (В различных источниках ζ называют также степенью завершенности стадии, числом пробегов стадии.) Основанный на химических переменных расчет позволяет вычислить количества неключевых веществ по начальному составу и известным количествам ключевых веществ. Однако, вопрос о том, сколько ключевых веществ следует задать, при этом, как правило, заранее не решается. Приведем пример, в котором будем считать, что реакция протекает гомогенно при постоянном объеме. Поэтому, рассмотрев единичный объем, можем считать, что количества веществ равны их концентрациям. INV ( S TN (S TK ) 1 , E N N K )C , инварианты химической реакции где: E N N K - единичная матрица размерности N NK , N– число веществ, NK- число ключевых веществ, С – вектор концентраций всех веществ. Пример: число двойных связей при диспропорционировании олефинов. Если q инвариантов ЛН, то (n-q) свободных переменных (gi) можно задать в качестве количеств ключевых реактантов (gкл). Остальные q количеств (gнекл) вычисляют как решения системы уравнений инвариантов. Max q=RkH, соответствующее nкл=RkA. Рассмотрим формально одностадийную реакцию: 2 СН3 Br + Mg = C2 H6 + MgBr2 . (3.21) В процессе реакции количества СH3 Br и Mg все время убывают, а количества C2 H6 и MgBr2 возрастают. Но существуют комбинации этих количеств, остающиеся неизменными (инвариантными). Эти комбинации называют инвариантами реакции. Так, для реакции (3.21) можно записать: Нетрудно обнаружить физический смысл записанных выражений: inv1 – общее число молей квазиатомов СН3 в системе, которое, разумеется, не меняется; точно так же inv2 – число молей атомов Mg, а inv3 – атомов Br. Но и любая линейная комбинация этих величин тоже будет инвариантом. Инварианты можно определить не только для одностадийных, но и для любых многостадийных реакций. Это делает их удобным инструментом анализа материальных превращений в реакционных системах. В частности, отмечу следующее. Пусть в реакционной системе имеется n веществ и пусть мы найдем q линейно независимых инвариантов. Тогда система инвариантов представляет собой q уравнений 1-й степени с независимыми левыми частями, содержащих n неизвестных. В этой системе можно выбрать (n – q) свободных переменных gкл, а оставшиеся q неизвестных gнекл будут найдены при заданных gкл как решение системы уравнений. Индексом «кл» здесь обозначены ключевые вещества, а индексом «некл» – неключевые. Таким образом, число неключевых веществ равно числу линейно независимых инвариантов q, а число ключевых равно n – q. Инварианты – это величины, имеющие для данных условий совершенно определенные численные значения, не изменяющиеся по ходу реакции. В частности, в начальный момент их значения те же, и если известен начальный состав системы, то исходя из него легко их вычислить. Наибольшее число линейно независимых инвариантов равно рангу атомной матрицы: q=r g h. (3.25) Наибольшее число неключевых веществ равно q, а число ключевых nкл=n – nнекл=n – q=r g a. (3.26) Один из простейших способов построения системы линейно независимых инвариантов – тот, который без особых объяснений был применен при записи системы (3.22) – (3.24): каждый инвариант получается как уравнение материального баланса по одному из атомов или квазиатомов (по одному из столбцов атомной матрицы): invr = Σ hprgp , (3.27) где суммирование ведется по столбцу r (по r-му атому); gp – количество вещества Ap . Ключевые и неключевые реактанты. С + О2 = СО2 , (3.1) С + СО2 = 2СО, (3.2) 2С + О2 = 2СО. (3.3) Рассмотрим реакции (3.1) – (3.3). Пусть вначале в системе содержался 1 моль С и 1 моль О2 , оксидов не было. И пусть в некоторый момент установлено, что в системе находятся 0,1 моль С и 0,1 моль СО. Можно ли, исходя только из этих данных, рассчитать для того же момента количества непрореагировавшего О2 и образовавшегося СО2 ? Оказывается, можно. В реакцию вступило 1 – 0,1 = 0,9 моль С. Из него на образование СО затрачено 0,1 моль. Значит, на образование СО2 пошло 0,8 моль; количество диоксида в данный момент равно тоже 0,8 моль. Расход молекул О2 на образование СО равен 0,1/2 = 0,05 моль, а на образование СО2 – 0,8 моль. Всего затрачено 0,85 моль О2 , осталось 1 – 0,85 = 0,15 моль О2 . Мы рассчитали: в заданный момент в системе есть 0,8 моль СО2 и 0,15 моль О2 . Те вещества, количества которых в данный момент заданы, называют ключевыми, а те, количества которых мы рассчитываем, – неключевыми. Заметим, что для начального момента должны быть известны количества и тех, и других веществ. Любое из веществ, участвующих в реакции, может выступать в роли и ключевого, и неключевого. Чаще всего ключевыми оказываются те вещества, количества (или концентрации) которых проще измерить. Есть две основные ситуации, в которых желательно отнести часть веществ к неключевым. Это, во-первых, обстановка эксперимента или контроля производства. Во-вторых, это этап записи и решения уравнений математического описания процесса. В основе большинства этих уравнений лежат балансы по отдельным веществам. Число таких уравнений равно числу веществ, причем они могут оказаться достаточно сложными (нелинейными, дифференциальными), поэтому целесообразно уменьшить их число. Этого можно добиться, записывая и решая уравнения только для ключевых веществ, а количества остальных веществ рассчитывать через ключевые. Степень превращения (конверсии), выход, селективность (, , ) по суммарному стехиометрическому уравнению. Конверсия χ характеризует глубину превращения исходного реагента, выход η – количество образующегося продукта, селективность σ – то, насколько целесообразно использована та часть реагента, которая превратилась в продукты (какая часть прореагировавшего реагента превратилась именно в нужный продукт). э=аА/аВ – эквивалент продукта по реагенту. =(gА0-gА)/gА0. =эgВ/gА0. =эgВ/(gА0-gА). Связи =, =/, =/. Предельные значения. Отсюда следует, что выход продукта равен степени превращения только при σ=1, т. е. при отсутствии побочных реакций, а во всех остальных случаях η < χ; далее, при χ=1 получаем η=σ, а при неполной конверсии η < σ. Как уже отмечалось, если реакция идет в гомогенной среде при постоянном объеме, то в формулах (3.33) – (3.35) можно заменить количества веществ на их концентрации. э = аА / аВ коэффициент эквивалентности, который показывает, какому числу молей А эквивалентен один моль В. Словесные определения как опора формульных. Прямая задача химического равновесия. Обратная задача химического равновесия. Косвенные измерения. Нелинейное оценивание. Одно из важнейших применений стехиометрического анализа – запись уравнений для расчета равновесия сложных (многостадийных) реакций. Такой расчет называют прямой задачей химического равновесия. Обратная задача равновесия формулируется так: получены опытные данные о свойствах систем, в которых установилось равновесие в интересующей нас реакции. Необходимо рассчитать константы равновесия для стадий этой реакции. Обычно мы можем измерить какие-то характеристики равновесного состава, зависящие от концентраций, причем чаще всего зависимость известна не полностью – мы не знаем ее параметров. И задача стоит в том, чтобы вычислить и неизвестные параметры этой зависимости, и константы равновесия. Метод наименьших квадратов. Вариационное исчисление как общая теория методов оптимизации. Метод наименьших квадратов - найти такие значения параметров, которые обеспечат минимум суммы где суммирование производится по всем значениям i (номерам опытов). Кинетика химических реакций. Механизм. Формальная кинетика химических реакций. Скорость химического превращения r=dgр/(Vdt). При постоянном объеме в закрытой системе r=dC/dt. Главной проблемой кинетики как раздела физической химии является вопрос о механизме реакции. Основная задача – раскрыть механизм реакции и установить, как он отражается в кинетических закономерностях. При анализе, описании и расчете протекания реакции как элемента химико-технологического процесса вопрос о механизме часто не возникает: кинетические закономерности рассматриваются как уже заданные (например, изученные на предыдущем физико-химическом этапе исследования). В этих случаях описание проводится на языке формальной (феноменологической) кинетики. Скорость реакции – основное понятие кинетики. Она определяется как количество вещества, реагирующее в единицу времени в единице реакционного пространства: где r – скорость реакции; dgp – количество вещества, превращающееся в результате протекания реакции за время dt (знак дифференциала dgp определяется тем, образуется или расходуется вещество – соответственно знаки «+» и «–»); V – реакционное пространство (объем в случае гомогенной реакции, поверхность – в случае гетерогенной). Далее в этом разделе будут рассматриваться в основном гомогенные реакции, поэтому V обозначает объем. Пользоваться уравнением (3.44) можно только при соблюдении двух условий: 1) реакция проходит при постоянном объеме; 2) объем этот можно считать закрытым. Закрытой, или замкнутой, называется система, которая по ходу процесса не обменивается веществом с окружающей средой (хотя и может обмениваться энергией). Большинство химико-технологических процессов, и в первую очередь все непрерывные процессы, протекают в открытых системах, которые характеризует обмен с окружающей средой энергией и веществом. Именно открытость аппарата непрерывного действия (ввод и вывод потока) обеспечивает непрерывность процесса. Реактор чисто периодического действия открыт в периоды загрузки и выгрузки, а при протекании реакции он замкнут. Особенность уравнений материального баланса для замкнутых систем: вход и уход вещества равны нулю. Поэтому единственной причиной изменения количества вещества в системе dg является химическое превращение: Смысл уравнения (3.47) следующий: в замкнутых гомогенных системах скорость реакции равна изменению концентрации во времени. Им часто пользуются, однако необходимо помнить, что это лишь частный случай, который верен далеко не для всех систем. Формально простая реакция. Сложные реакции: обратимые, последовательные, параллельные, их комбинации. Независимость протекания реакций. Химическая кинетика определяет простые (одностадийные) реакции как такие, которые по существу проходят в одну стадию; простая реакция содержит один элементарный акт. Однако такие реакции, которые проходят как истинно одностадийные, встречаются редко. В феноменологической кинетике оказывается удобным говорить о формально простых реакциях. Так называют реакции, которые можно формально пред ставить как протекающие в одну стадию. По существу реакция может быть сложной, проходящей через какие-то промежуточные стадии, но если в условиях рассматриваемой задачи промежуточные продукты не обнаруживаются, то реакция будет считаться формально простой. Можно выделить три простейших типа сложных реакций. 1. Обратимая реакция: с излагаемой точки зрения она – сложная, состоящая из двух стадии: прямой и обратной реакций, хотя ряд авторов предпочитает говорить о них, как о частном случае формально простых реакций. 2. Параллельная реакция: исходное вещество по двум или нескольким параллельно протекающим реакциям (стадиям) превращается в два или несколько продуктов. Примером может служить нитрование толуола с параллельным получением о- и пнитротолуолов. 3. Последовательная реакция: стадии реакции следуют одна за другой, продукт первой стадии является исходным веществом второй и т. д. Примером может служить полимеризация с последовательным присоединением молекул мономера к растущей макромолекуле. Остальные сложные реакции можно представить в виде комбинаций указанных трех типов, например последовательно-параллельные, последовательные реакции с обратимыми стадиями и т. д. Процесс протекания многостадийных реакций, стадии которых разделены во времени, т.е. сначала проводится одна стадия, затем через некоторое время – вторая и т. д считаются несколькими независимыми реакциями. А сложные реакции, которые перечислены в пунктах 1-3 (параллельная, последовательная, обратимая), проходят так, что в реакционной смеси одновременно идут все стадии и присутствуют исходные вещества и продукты всех стадий. Скорость простой реакции (стадии) r=d/(Vdt) – определение ИЮПАК. Рассмотрим формально одностадийную реакцию (она может быть и одной из стадий сложной реакции): Возникает следующий вопрос: количество какого вещества (А, В или С) следует вводить в уравнение (3.44) при определении скорости реакции (3.48)? Ответ на этот вопрос легко получить из понятия стехиометрической эквивалентности. Если за какой-то промежуток времени прореагирует некоторое количество –dgA вещества А (знак минус означает, что вещество расходуется), то за это же время количества прореагировавшего В и образовавшегося С составят: Поэтому, подставив в формулу (3.44) один раз dgA, другой раз dgB, третий раз dgC, получим три значения: rА, rB и rC, отличающиеся одно от другого постоянными множителями. Строго говоря, это одна и та же величина – скорость реакции (3.48), но выражена она в разных единицах. Для единообразия скорость одностадийной реакции, или скорость стадии, принято определять путем деления скорости, выраженной через любое вещество J, участвующее в данной стадии, на стехиометрический коэффициент этого вещества. В таком случае безразлично, какое из веществ принято в качестве J. Сопоставление с формулой (3.19) показывает, что скорость стадии можно записать через химическую переменную ζ: Но при записи уравнений материального баланса важно пользоваться величинами скорости реакции, отнесенными к определенным веществам rJ . Такие скорости очень просто получаются из уравнений (3.50) и (3.19): rJ = aJ r. (3.51) здесь коэффициент aJ может быть как положительным, так и отрицательным или равняться нулю (например, если J – катализатор). Порядок реакции по веществу, общий, константа скорости. r=kCAnACBnB. Словесное обозначение. Уравнение Гульдберга и Вааге (не закон). Скорость многих (хотя и не всех) формально простых реакций, в том числе многих стадий сложных реакций, пропорциональна концентрациям реагирующих веществ в некоторых степенях. Показатель степени в таком случае называют порядком реакции по реагенту. Так, для реакции aAA + aBB → продукты соответствующая зависимость будет выражаться кинетическим уравнением где n1 – порядок реакции по веществу А; n2 – порядок реакции по веществу В. Сумму n1 + n2 называют общим, или суммарным, порядком. Коэффициент пропорциональности k именуют константой скорости реакции. Порядок реакции или стадии буду иногда обозначать цифрой над (или под) стрелкой, указывающей направление реакции; здесь же приведу обозначение константы скорости. Так, запись обозначает обратимую реакцию, у которой прямая стадия имеет 1-й порядок по А и константу скорости k1 , обратная – 2-й порядок по С и константу k2 . Поскольку порядок по В не указан, значит, он – нулевой. Достаточно часты случаи, когда порядок по каждому из реагентов совпадает с его стехиометрическим коэффициентом. Но такое совпадение обязательно лишь для строго (не формально) простых реакций. Закон действующих масс в кинетической форме (основное уравнение кинетики) гласит, что скорость элементарной химической реакции пропорциональна произведению концентраций реагентов в степенях, равных стехиометрическим коэффициентам в уравнении реакции. Это положение сформулировано учёными К. Гульдбергом и П. Вааге. Для элементарной химической реакции: Температурная зависимость скорости реакции. Уравнение Аррениуса. k=Ae-E/RT. lnk=lnA-E/RT. Предэкспоненциальный множитель и энергия активации – активационные параметры. Порядок реакции иногда претерпевает изменения с ростом температуры, но это скорее исключение, чем правило. Наиболее тесно с температурой связана константа скорости реакции. Эта зависимость может быть описана уравнением Аррениуса: Параметрами уравнения (3.53) являются предэкспоненциальный множитель, или предэкспонента, А и энергия активации Е. Существует мнение, что чем больше энергия активации, тем, в соответствии с формулой (3.53), меньше величина k и, значит, медленнее реакция. Однако это мнение неверное. Величина k определяется совокупностью значений Е и А, поэтому сама по себе величина Е еще не определяет, быстро или медленно проходит реакция. В химической кинетике существует изокинетическое правило (правило компенсации): почти всегда чем больше энергия активации, тем больше предэкспонента. Реакция с меньшей Е имеет и меньшее значение А, а влияния обоих параметров противоположны. Формальный (феноменологический) смысл E иной. Прологарифмируем уравнение (3.53): Получили линейную зависимость ln k от 1/Т, коэффициентами которой являются ln A и – E/R. Изобразим ее на графике для двух реакций: у первой величина E меньше (и, согласно изокинетическому правилу, ln A тоже меньше), чем у второй (рис. 3.1,а). Из рис. 3.1,а очевидно, что при высоких температурах (значение 1/Т мало, область близка к оси ординат) больше константа скорости той реакции, у которой энергия активации больше. При низких температурах больше константа скорости реакции с малой энергией активации. Те же зависимости, но в координатах T – k представлены на рис. 3.1,б. Полученную закономерность можно сформулировать так: чем больше энергия активации, тем сильнее скорость реакции зависит от температуры. Такой характер влияния Е на прохождение реакции позволяет произвести быструю качественную оценку влияния температуры на ход некоторых сложных реакций. Так, для обратимых экзотермических реакций Е2 > Е1 : энергия активации обратной реакции больше, чем прямой. Поэтому с ростом температуры коэффициент k2 растет быстрее, чем k1 , в результате чего равновесие смещается влево. При эндотермических обратимых реакциях наоборот Е2 < Е1 , и с ростом температуры равновесие смещается вправо. Так устанавливается связь уравнения Аррениуса с правилом Ле Шателье. Если рассматривается сложная реакция, некоторые стадии которой являются для нас побочными, то соотношение энергий активации различных стадий определяет влияние температуры на селективность: при нагревании преимущественно ускоряются те стадии, которые характеризуются большей энергией активации. Нужно иметь в виду, что в одном важном случае снижение энергии активации действительно приводит к ускорению реакции – это катализ. Механизм действия катализатора связан со снижением энергии активации реакции. Конкуренция целевых и побочных стадий при изменении температуры. Суммирование по реакциям. rj=Sumi=1,mrji=Sumi=1,majiri. Для всех типов формально сложных реакций, кроме простейшей обратимой, понятие общей скорости реакции не имеет смысла. Реакция состоит из ряда стадий, каждая из них имеет свою скорость, и нельзя достаточно естественным образом определить, что такое скорость всей сложной реакции в целом. В то же время любое из участвующих в реакции веществ образуется или расходуется с определенной скоростью, причем знание этой скорости обязательно при расчете процесса. Скорость сложной реакции по любому веществу J равна алгебраической сумме скоростей всех стадий по этому веществу (с учетом стехиометрических коэффициентов): Скорость стадии по веществу можно определить по формуле (3.51). Если вещество в стехиометрии стадии не участвует, его стехиометрический коэффициент в этой стадии равен нулю. Прямая и обратная задача химической кинетики. Прямая задача химической кинетики – расчет зависимости от времени концентраций веществ в реакционной смеси при известных кинетическом уравнении, значениях констант скорости, начальном составе. Особенность таких задач состоит в том, что перечисленных данных недостаточно. Необходимо учесть также характер движения потока, в котором проходит реакция, а в случаях гетерогенных реакций также характер диффузии веществ в зоне реакции. Обратные задачи кинетики имеют очень сложную специфику. Дело в том, что, как уже отмечалось, реально все химические реакции сложны, проходят через ряд промежуточных стадий. Обратная задача заключается в расшифровке механизма реакции, определении ее маршрута: стадий, через которые она проходит, и кинетических характеристик этих стадий. Обратная задача может быть сформулирована как задача дискриминации : нужно отбросить все механизмы, кроме одного истинного. Из-за того что предполагаемых механизмов много, часть из них, в том числе и далеких от истинного механизма, может показывать результаты, близкие к истинным. Решение таких задач требует больших объемов исследования, применения специальных методов планирования эксперимента и метода наименьших квадратов в варианте нелинейного оценивания. Качественный анализ хода реакции. Асимптотические оценки. Правило Лопиталя. Температурная зависимость в качественном анализе. Одна из возможностей качественного анализа опирается на асимптотические оценки – оценки поведения функций в крайних областях значений аргумента. В рассматриваемом случае целесообразно в качестве аргумента принять время t, причем крайние области его значений – это t = 0 и t → ∞. В качестве примера проанализируем протекание реакции. Целевым продуктом является вещество В. Примем следующие условия. Реакция проходит в замкнутой системе (можно показать, что качественные выводы окажутся такими же и для открытой системы, но для замкнутой анализ проще). Объем и температура постоянны. Начальная концентрация реагента сА0= 1 моль/л. В начале процесса продукты отсутствуют. Известны энергии активации первой и второй стадий: Е1 = 45000 и Е2 = 75000 Дж/моль соответственно. Вначале выясним, какими станут концентрации веществ, если время процесса очень велико (t → ∞). При этом обе реакции дойдут до конца, поскольку и та, и другая необратимы. Веществ А и В не останется, а концентрации С и Н определятся стехиометрией: 2 и 2 моль/л. Затруднение возникает при оценке предела σ, когда t→ 0. Формулы (3.35) и (3.36) приводят к выражению вида 0/0, т.е. к неопределенности. Раскрыть эту неопределенность можно по правилу Лопиталя, заменив функции в числителе и знаменателе их производными по времени. Для замкнутой системы производная от концентрации по времени равна скорости реакции. При этом учтем, что начальная концентрация – величина постоянная (в данном случае равная 1), а производная от постоянной равна 0. Учтем также то, что при t → 0 cB → 0. Получаем: Можно показать, что и в открытой системе предел окажется таким же. Физический смысл этого результата прост. При малом времени процесса скорость первой стадии реакции высока, так как велика концентрация А, а скорость второй стадии очень мала (из-за малости сВ) и стремится к 0 при t → 0. Поэтому в пределе реакция проходит так, как будто побочной стадии нет; а в отсутствие побочной стадии селективность равна 1. Если бы побочная стадия была параллельной, рассматриваемый предел был бы меньше 1. Зная величины констант скорости, его можно было бы рассчитать; в противном случае пришлось бы констатировать, что селективность стремится к некоторой величине σ0 , причем 0 < σ0 <1. Полученные нами асимптотические оценки не содержат температуры ни в явном, ни в неявном виде. Это верно для рассматриваемой реакции, но в других случаях выражения для пределов могут содержать константы скорости или константы равновесия – тогда температура будет влиять и на асимптотические оценки. Для рассматриваемой реакции пределы при любых температурах одни и те же, изменяются характеристики зависимостей между этими пределами. Для показателей χ и σ изменения просты. С ростом температуры скорость первой стадии реакции растет, поэтому кривая для χ вначале идет круче и быстрее приближается к предельному значению. Скорость второй стадии реакции, обусловливающей падение селективности, тоже растет, и кривая зависимости σ(t) падает круче сначала и быстрее переходит в область очень малых значений. Что же касается зависимости η(t), то здесь наибольший интерес представляет точка максимума, обе ее координаты – время достижения максимума и максимальное достигаемое значение η. Для качественной оценки влияния температуры на время достижения максимума достаточно учесть, что с ростом температуры ускоряются обе стадии. При этом выход продукта будет быстрее расти и быстрее падать – максимум сместится к меньшему времени. Чтобы оценить, как при этом изменится высота максимума, учтем следующее. Искомая высота определяется конкуренцией обеих стадий: первая увеличивает η, вторая уменьшает. С ростом температуры обе стадии ускоряются, но вторая – сильнее, потому что Е2 > Е1 . В результате повышение температуры приведет к снижению максимального значения η. 3. Процессы в потоке. Идеальные потоки. Поток как гомогенная движущаяся жидкая среда в аппарате непрерывного действия. Гетерогенность, влияние потока в иерархии: вниз на перенос, вверх на рабочую зону. Сложная структура потока: поле скоростей, перемешивание вдоль и поперек, время пребывания (объемная скорость) среднее и фактическое, проблема усреднения показателей. Сложность структуры потока. Любой поток сложен по своей структуре. Сложность проявляется на различных уровнях, в разных масштабах, проявления ее весьма многообразны. Рассмотрим некоторые из них. Нестационарность скорости. По этому признаку, как известно, потоки делятся на ламинарные и турбулентные. Ламинарный поток преимущественно стационарен. Разумеется, при изменениях, происходящих в системе (прежде всего при изменениях расхода жидкости), стационарность нарушается. Но установившийся ламинарный поток стационарен: в данной точке аппарата скорость проходящего через нее потока остается одной и той же. Турбулентный поток нестационарен по существу. Даже если никакие параметры в среднем не меняются во времени, поток все время испытывает хаотические колебания скорости, так называемые флуктуации, или пульсации. Неоднородность поля скоростей. В разных частях потока скорости частиц жидкости различны как по величине, так и по направлению. Эти различия могут быть стационарными (например, параболический профиль скоростей в ламинарном потоке) и нестационарными: в турбулентном потоке максимум скорости наблюдается то в данной точке, то в соседней. Крайние случаи неоднородности скоростей – это, с одной стороны, байпасы, а с другой – застойные зоны. В нашем случае под байпасом понимается часть потока, очень быстро проходящая от входа к выходу, почти не участвуя в процессе. Порции жидкости, попавшие в застойную зону, напротив остаются практически неподвижными и также выпадают из процесса. Неоднородность скоростей по направлению может проявляться поразному. В турбулентном потоке флуктуации скорости направлены не только вдоль, но и поперек потока. Кроме того, и в ламинарных, и в турбулентных потоках могут образовываться зоны циркуляции жидкости. Описанные особенности структуры потока приводят к двум взаимосвязанным явлениям, оказывающим сильное влияние на ход химико-технологических процессов: возникновению перемешивания текущей жидкости и неравномерности времени пребывания. Традиция, существующая в химии, склонна всегда считать перемешивание жидкости фактором, способствующим протеканию реакции. Но при рассмотрении этого фактора следует различать два случая: перемешивание в поперечном и в продольном относительно потока направлениях. Поперечное перемешивание интенсифицирует массообмен между осевой частью (ядром) потока и его периферией и тем самым, как правило, улучшает условия протекания реакции. Продольное перемешивание – это смешение частиц, которые недавно вошли в аппарат, с частицами, давно в нем находящимися, в которых процесс уже зашел далеко; чаще всего оно снижает движущую силу процесса и ухудшает его показатели. Поперечное перемешивание возникает либо под действием перемешивающих устройств (мешалок, устройств для барботажа и др.), либо под влиянием турбулентных пульсаций скорости, а также при наличии зон циркуляции. Те же факторы вызывают и продольное перемешивание, но в этом случае, как правило, появляется еще сильно влияющий фактор – неравномерность распределения скоростей: те частицы, которые вследствие большей скорости ушли вперед, смешиваются с идущими впереди, отставшие – с нагоняющими их сзади. Очень часто именно эта неравномерность вносит основной вклад в продольное перемешивание. В ламинарном потоке оно может оказаться существенно бóльшим, чем в турбулентном. Так, при течении капельной жидкости в трубе переход от ламинарного режима (Re = 2000) к турбулентному (Re = 100 000) приводит к уменьшению интенсивности продольного перемешивания на несколько порядков. Неравномерность времени пребывания – явление, в значительной мере эквивалентное продольному перемешиванию. Для частиц, уходящих вперед, время пребывания меньше среднего. Отстающие частицы характеризуются бóльшим временем пребывания. Среднее время пребывания t текущей жидкости в аппарате, получаемое усреднением времен пребывания разных частиц, определяется простым соотношением: Ее интерпретируют как объем движущейся фазы, проходящий через единицу объема аппарата за единицу времени. Может показаться, что учитывать неравномерность времени пребывания частиц вещества необязательно: при малом времени пребывания частиц в рабочей зоне реакция пройдет недостаточно глубоко, зато если частицы долго находятся в этой зоне, то глубина протекания реакции велика. На выходе частицы взаимно перемешиваются, и степень превращения усредняется. Возникает вопрос: можно ли рассчитывать концентрации подстановкой в решение дифференциального уравнения кинетики значения t , пренебрегая неравномерностью t ? Оказывается, что при одном и том же среднем времени пребывания частиц различные степени неравномерности дадут разные результаты. Протекание химической реакции при неравномерном времени пребывания частиц вещества. Частицы с малым временем пребывания выносят из аппарата много не прореагировавшего вещества, что снижает степень превращения. Правда, в частицах, долго находившихся в аппарате, реакция проходит очень глубоко. Но скорость большинства реакций снижается во времени. В этих частицах скорость реакции уже столь мала, что увеличение времени пребывания слабо сказывается на превращении. Проигрыш из-за быстро «проскочивших» через аппарат частиц не компенсируется выигрышем за счет частиц, задерживающихся в нем. Можно предложить разные подходы к изучению структуры потока и влияния этой структуры на ход химических процессов. Наиболее полную информацию о структуре потока можно получить, зная скорость жидкости в любой точке аппарата, т. е. анализируя поле скоростей. В принципе это дает исчерпывающую картину потока. Точное описание поля скоростей может явиться материалом для решения любой задачи, относящейся к течению жидкости. Но при таком подходе возникают труднопреодолимые препятствия. Прежде всего чрезвычайно трудна экспериментальная задача измерения скоростей во всех частях потока. В любом аппарате имеются области, где поток либо проходит сквозь сужения, либо резко заворачивает. Здесь почти невозможно измерить скорость, не нарушив структуру потока. Но едва ли не важнее то, что знание поля скоростей позволяет решать практические задачи лишь в принципе. Как правило, это решение оказывается настолько сложным, что львиной долей информации воспользоваться не удается. Поле скоростей – сложная трехмерная структура, описание которой должно содержать функции по меньшей мере трех переменных (координат). Нестационарность (например, в турбулентном потоке) добавляет четвертую переменную – время. Математическое описание процесса обычно получается в виде систем нелинейных дифференциальных уравнений в частных производных. Решить такую систему даже с помощью мощных компьютеров удается лишь в простейших случаях. Идеальные потоки без параметров или с минимумом таковых: вытеснения и смешения. Адекватность практическим представлениям, свойства, технологичность. Еще один подход – построение упрощенных мысленных моделей потока. Упрощая сложную картину, такая модель должна в то же время отражать существенные для нас особенности потока, в первую очередь адекватно описывать особенности протекания в данном потоке химических, тепловых и массообменных процессов. Как и в других областях науки, в этом случае можно построить модели разной степени упрощения (см. разд. 1.3). На первом этапе создаются максимально упрощенные модели, которые называют идеальными потоками. Разработаны две модели идеальных потоков: идеальное вытеснение и идеальное смешение. Здесь отметим одну особенность этих моделей: они не содержат никаких параметров, отражающих специфику структуры потока. Единственный параметр – среднее время пребывания, определяемое пo формуле (4.1). В этом смысле все потоки идеального вытеснения подобны один другому; то же самое относится к потокам идеального смешения. Существует довольно много задач, в которых описание реального потока моделью того или другого идеального потока оказывается достаточно точным. Если же точность такого приближения недостаточна, то переходят к более сложным моделям неидеальных потоков. Эти модели уже содержат параметры, описывающие характер потока, начиная от однопараметрических моделей и кончая сложными комбинированными моделями, где число параметров может быть велико. Описанию некоторых таких моделей посвящен разд. 4.4. Рассматривая какую-либо модель, я буду стараться осветить три вопроса: 1. Реалистичность и адекватность модели, т.е. насколько наша модель соответствует реальным объектам? 2. Свойства модели. Какая математическая модель соответствует данной схеме потока, каковы особенности решения уравнений математического описания и какие свойства объекта определяются этими решениями? 3. Технологическая оценка. Хорошо или плохо влияют на технологические показатели те или иные особенности объекта, описываемого моделью? Этот подход относится как к моделям потоков, так и ко всему дальнейшему изложению. ИВ (идеальное вытеснение): одномерный поток с одинаковой скоростью (концентрацией, температурой), временем пребывания. Малый объем поперечного сечения потока является замкнутым. r=dC/dt. Переменный объем (переменное сечение) добавляет одно слагаемое. В аппарате идеального вытеснения поток движется совершенно равномерно. В любом поперечном сечении все частицы имеют одинаковую скорость (рис. 4.1). Фронт потока движется, как твердый поршень, поэтому такой поток иногда называют поршневым (от англ. piston-flow). Рис. 4.1. Схема потока идеального вытеснения Рис. 4.2. Схема движения малого объема в потоке вытеснения При анализе сложных процессов (например, реакций, проходящих с выделением и отводом тепла) определение идеального вытеснения приходится несколько конкретизировать – добавляется еще одно свойство. Не только скорость, но и концентрации, и температура в таком потоке выровнены по поперечному сечению. Для изотермических процессов эта выровненность получается автоматически, если выровнены скорости. Для описания, анализа и расчета процессов существенны два следствия из определения идеального вытеснения. 1. Время пребывания всех частиц в потоке идеального вытеснения одинаково. Это практически единственный мыслимый поток, для которого формула (4.1) определяет не только среднее, но и конкретное время пребывания любой движущейся через аппарат частицы жидкости. 2. Выделенный в потоке малый объем, занимающий все поперечное сечение и движущийся вместе с потоком (рис. 4.2), в случае идеального вытеснения можно рассматривать, как замкнутый. Действительно, в процессе течения ни одна частица не выйдет из этого объема ни вперед, ни назад (для этого она должна была бы двигаться с иной скоростью, чем остальные). Точно так же ни одна частица не войдет в рассматриваемый объем из таких же объемов, примыкающих к нему спереди и сзади. Поэтому кинетика реакции при постоянном объеме будет описываться уравнениями Если объем непостоянен, то выражения усложняются, но в принципе в любом случае можно записать соответствующую систему дифференциальных уравнений. Субстанциональная производная – начало координат движется с объемом. Обычная производная равна нулю. Поверка/проект. Реакция 1 порядка как простой пример. В уравнении (4.3) есть одна тонкость. Время, входящее в него, отсчитывается в объеме, движущемся вместе с потоком. Поэтому в его левой части – не совсем обычная производная: дифференцирование производится для движущейся вместе с субстанцией системы координат. Это субстанциональная производная. Если измерять концентрацию любого вещества, находясь неподвижно в любой точке аппарата, то получим обычную производную. Ясно, например, что в стационарном режиме концентрация любого вещества в этой точке не меняется во времени: подходя к ней, жидкость всякий раз приобретает одно и то же значение концентрации, поэтому обычная производная равна нулю. Но субстанциональная производная и в стационарном режиме – не нулевая, поскольку при прохождении данной точки реакция в движущейся жидкости продолжает идти. Необходимо учитывать, что интегрирование субстанциональных производных ничем не отличается от интегрирования обычных. Решение системы (3.47) следует искать в пределах от t = 0 (жидкость вошла в аппарат) до (выход жидкости из аппарата). В этом случае получатся концентрации веществ на выходе из аппарата. Это поверочный расчет. Для проектного расчета в решение системы подставляют требуемые значения концентраций и находят , а затем по формуле (4.1) определяют объем аппарата. Реакция 1 порядка как простой пример. ИС (идеальное смешение): кинетика в точечном объеме выполняется во всем объеме. Входной скачок. Среднее время пребывания. Открытость:rdC/dt. Субстанция j, контур – аппарат, время dt. Вход Вj=cj0vdt. Уход Уj= cjvdt. Иj-Сj=Varjdt. Накопление Нj=Vadcj. В итоге cj0v-cjv+Varj=Vadcj/dcj. Теперь опишем аппарат идеального смешения. Представим себе аппарат с мешалкой, через который проходит поток жидкости (рис. 4.3). Мощность мешалки такова, что поступающая жидкость мгновенно перемешивается с массой, уже находящейся в аппарате. Таким образом, все, что попадает в аппарат идеального смешения, мгновенно равномерно распределяется по всему его объему. Рис. 4.3. Концентрации веществ на входе, в объеме и на выходе аппарата смешения; v – расход потока Перечислю важнейшие следствия из этого определения. 1. Концентрации всех веществ и температура равномерно распределены по объему аппарата. В любой паре точек в аппарате любая из этих величин имеет в данный момент одно и то же значение. 2. Для уточнения следствия 1 следует рассмотреть две точки, о которых заранее трудно сказать, находятся ли они в аппарате: точки входа и выхода потока. На выход поток выносит ту жидкость, которая находится в аппарате. Поэтому на выходе из аппарата идеального смешения концентрации и температура те же, что и в объеме. На входе в аппарат концентрации и температура претерпевают скачок: исходные значения параметров потока, мгновенно смешивающегося с содержимым аппарата, соответственно мгновенно изменяются до тех значений, которые характеризуют режим внутри аппарата и на выходе из него. 3. Время пребывания в аппарате идеального смешения распределено неравномерно. Действительно, распределяя по объему вошедшую порцию жидкости, наша идеальная мешалка пошлет некоторые частицы из этой порции к выходу и они сразу уйдут из аппарата, в то время как другие, попавшие в иные части аппарата, могут задерживаться в нем весьма надолго. 4. Аппарат, как и любая его часть, принципиально открыт. Смешение в каждый момент и в каждой точке подводит одни порции жидкости и отводит другие. Замкнутых объемов нет. Отсюда следует, что зависимости (3.47) к потоку смешения неприменимы. Для его описания следует искать иной подход. Здесь можно использовать то обстоятельство, что во всех точках аппарата концентрации и температура, а стало быть, и скорость реакции одинаковы. Аппарат идеального смешения – типичный пример объекта с сосредоточенными параметрами (см. разд. 1.3). Это позволяет очень просто записать уравнения баланса (1.11) или (1.12). Дело в том, что во всех точках такого объекта интенсивность источника (или стока) – одна и та же. В результате весь объем аппарата можно рассматривать как элементарный объем. Воспользуемся рис. 3.3 и составим схему материального баланса по веществу J. Символ J будет означать «какое-либо из веществ», и все, что получено для него, верно в общем виде для любого из участников реакции. Таким образом, уже выбраны субстанция (вещество J) и контур, охватывающий весь аппарат. Выберем в качестве интервала времени дифференциал dt и обсудим статьи баланса. Вход. За время dt в аппарат входит объем жидкости vdt. Умножив этот объем на концентрацию входящей жидкости, получим Уход. Определяем так же, как вход, при этом учитываем, что концентрация cJ имеет одно и то же значение как на выходе из аппарата, так и в любой точке внутри него. Таким образом, Источник и сток. Вспомним, что мы определили скорость реакции как количество вещества, превращающегося в единицу времени в единице объема. При этом формула (3.55) определяет скорость по веществу, так что в нее входят и стадии, в которых вещество образуется (источник J), и те, где оно расходуется (сток). Поэтому, умножив скорость по J на объем аппарата и на интервал времени, получим разность источника и стока: Накопление. Если за время dt концентрация изменится на величину dcJ , то изменение количества вещества в объеме (накопление) составит Нестационарное и стационарное поведение, со средним временем. Размерность системы уравнений. Открытость/закрытость. Варианты записи. Стационарный режим при измерении скорости реакции. Каждая из формул (4.32) и (4.33) задает систему уравнений, поскольку ее следует записать для каждого из веществ, участвующих в реакции. Но в случае стационарного процесса часть уравнений (4.33) целесообразно заменить уравнениями стехиометрических инвариантов. Обратим внимание на одну особенность выражения (4.32). В его правой части – производная от концентрации по времени, умноженная на объем, а в левой на объем умножена скорость реакции, но имеются еще два члена. Отсюда следует, что практически никогда в таком потоке скорость реакции не равна производной dc/dt. Это объясняется открытостью данной системы. Лишь если мы исключим поток (приравняем v к нулю), т.е. замкнем объем, эти две величины сравняются и мы перейдем к описанию периодического процесса – выражению (4.3). Если поделить выражения (4.32) и (4.33) на v и учесть соотношение (4.1), то получим формулы, часто более удобные для расчетов: В стационарном режиме в потоке смешения скорость реакции может быть получена как отношение конечного изменения концентрации к среднему значению времени, за которое изменение произошло. Следует лишь учесть, что в нестационарном режиме это соотношение неверно. Рассмотрим сравнительно простой случай – стационарное протекание реакции в потоке идеального вытеснения. Это будет иной подход по сравнению с тем, что применен выше. Так как мы считаем в идеальном вытеснении параметры выровненными в поперечных направлениях, то изменения происходят только вдоль продольной оси х. Поэтому элементарный объем может занимать все поперечное сечение аппарата, но будет иметь бесконечно малую длину dx (рис. 4.4). Обратите внимание на различие между схемами на рис. 4.2 и 4.4. На рис. 4.2 изображен малый движущийся объем жидкости, на рис. 4.4 – малая неподвижная часть аппарата, через которую проходит поток. Рис. 4.4. Элементарный объем в аппарате идеального вытеснения Преимущество ИВ. Качественные сопоставления: концентрационная (порядок), температурная (энергия активации) зависимость Сопоставление идеальных потоков. О реалистичности моделей идеальных потоков. Идеальные потоки – сильно упрощенные модели. Примеры: Так, к идеальному вытеснению близок поток жидкости или газа, проходящий через достаточно длинный аппарат, заполненный слоем зернистого материала (насадочная колонна, реактор с неподвижным слоем катализатора, шахтная печь). Зернистый слой интенсивно выравнивает поток. В меньшей степени можно применить эту модель к потоку в пустой трубе, особенно в ламинарном режиме (см. разд. 4.1). Близко к идеальному смешению течение жидкости через аппарат с достаточно мощной мешалкой или через барботажный слой. В том же барботажном слое течение газа плохо описывается данной моделью, но зачастую нам нужно описать именно движение жидкости, считая, что газ не сильно отклоняется от идеального вытеснения. Сопоставление идеальных потоков. Каждый из идеальных потоков отличает предельная равномерность. В идеальном вытеснении это равномерность скоростей и времени пребывания, в идеальном смешении – равномерность концентраций и температуры по объему. Стационарный процесс в потоке идеального вытеснения описывается системой дифференциальных уравнений (4.3). Для идеального смешения этот случай описывается уравнениями (4.33) или (4.35) – конечными уравнениями, не содержащими операторов дифференцирования. Лишь в нестационарном режиме в описании появляются производные. Объясняется это тем, что в идеальном смешении нулю равны производные по координатам – градиенты концентраций и температуры. В связи с этим процесс в потоке смешения можно описывать так, будто он целиком происходит в одной точке (от точки к точке ничто не меняется). И в нестационарном процессе аппарат идеального смешения ведет себя «как точка» – все изменения происходят во всем объеме одновременно. Аппарат идеального вытеснения – объект с распределенными параметрами: в нем параметры процесса меняются от точки к точке. Правда, это простейший из таких объектов – одномерный, поскольку рассматриваются изменения лишь в продольном направлении, а поперек потока все считается выровненным. Тем не менее описание идеального смешения еще проще, что привлекательно с точки зрения математической обработки модели. Поэтому, как увидим далее, ряд более сложных моделей строится на основе модели смешения. Теперь посмотрим на примере простейшей реакции 1-го порядка А → В, как равномерность или неравномерность распределения параметров влияет на ход химической реакции. Многие сделанные при этом выводы будут верны для большинства формально простых реакций, обратимых реакций, а также для процессов массо- и теплообмена, описание которых аналогично описанию обратимой реакции 1-го порядка. В начале проведем качественный анализ. Равномерность времени пребывания в идеальном вытеснении способствует глубокому протеканию реакции (см. пример 4.1), так что с этой точки зрения преимущество следует отдать потоку вытеснения. Для того чтобы определить, как влияет на процесс равномерность концентраций в потоке смешения, построим график изменения концентрации реагента А по длине аппарата идеального вытеснения либо идеального смешения (рис. 4.5). На графике х = 0 – вход в аппарат; х = L – выход. Значения х < 0 и х > L соответствуют трубам, подводящим жидкость к аппарату и отводящим прореагировавшую смесь. Будем считать заданными исходную cA0 и конечную cAк концентрации реагента. Рис. 4.5. Изменение концентрации реагента по длине аппарата для идеальных потоков В идеальном вытеснении легко связать пройденный частицей путь с временем протекания реакции в этой частице: Уравнение (4.14) соответственно получит вид В аппарате смешения картина совершенно иная. На входе происходит скачок концентрации реагента А до значения, которое дальше сохраняется вплоть до выхода. По всей длине аппарата Если теперь рассмотреть любое поперечное сечение обоих аппаратов, то очевидно, что значение сА в аппарате вытеснения окажется больше соответствующего значения в аппарате смешения. Скорость реакции, пропорциональная сА, во всех сечениях аппарата, кроме последнего (на выходе), также будет большей в аппарате вытеснения, чем в аппарате смешения. Получить картину, показанную на рис. 4.5 (одинаковые начальные и одинаковые конечные сА), можно только в том случае, если объем аппарата смешения больше объема аппарата вытеснения. Отсюда можно сделать два вывода: 1) аппарат вытеснения обеспечивает большую эффективность процесса; 2) на кинетику реакции влияет не только химизм, но и характер потока. Таким образом, анализ распределения и времени пребывания, и концентраций приводит к выводу о большей эффективности потока вытеснения. Правда, судить об эффективности только по скорости протекания реакции опасно. Конструкции аппаратов, близких к обоим идеальным типам, различны. В частности, интенсивное перемешивание способствует массо- и теплообмену. Часто процессы, для которых важен перенос тепла и вещества, проще оформить в аппарате с перемешиванием, и тогда возникает проблема: чем жертвовать – простотой конструктивного оформления или малым продольным перемешиванием. Сопоставление произвольной реакции в потоках ИВ и ИС вычислительными методами: равная конверсия (высокая и низкая), равный объем, равная скорость. Наилучший и наихудший поток. Для 0, 1 и 2 порядка еще возможно аналитическое решение. Решение вопроса об эффективности того или иного потока должно, разумеется, базироваться на количественных оценках, к которым мы и перейдем. По-прежнему будем анализировать реакцию 1-го порядка А → В. Можно сопоставить выражения (4.14) и (4.39). Задав ряд значений , .рассчитаем при каждом из них степень превращения в потоках идеального вытеснения χвыт и идеального смешения χсм. Данные расчета сведены в следующую таблицу. Результаты последнего сопоставления очень показательны. Если требуется невысокая степень превращения (менее 0,9), то проигрыш вследствие перехода от идеального вытеснения к идеальному смешению не слишком велик. Оценивая эффективность, нужно учитывать и иные факторы. Но если требуется степень превращения 99% или выше, различие в необходимых объемах столь велико (в десятки или даже сотни раз), что ясно: следует применять аппараты, максимально близкие к идеальному вытеснению. Вывод о том, что в аппарате вытеснения глубина превращения выше, чем в аппарате смешения, и что преимущество этого потока возрастает по мере роста требуемой степени превращения, верен для изотермических необратимых и обратимых реакций любого положительного порядка, а также для большинства тепло- и массообменных процессов. Можно показать, что по глубине протекания процесса поток идеального вытеснения теоретически наилучший всегда, когда скорость процесса снижается по мере его протекания. Ускорение: автокатализ, разветвление цепи, биохимические, автотермические, матричные реакции. Нужно также иметь в виду, что существует ряд процессов, в которых закон изменения скорости реакции по ходу процесса иной. Вначале скорость реакции мала, постепенно она нарастает и затем, достигнув максимума, начинает снижаться (рис 4.6). Объясняется это тем, что во время процесса вырабатывается какая-либо субстанция (вещество или энергия), ускоряющая его протекание. Вначале этой субстанции мало, поэтому процесс идет медленно. С течением времени он самоускоряется до максимума, после чего скорость начинает уменьшаться вследствие нехватки исходного вещества. Отмечу четыре группы таких процессов. Рис. 11.6. Изменение по времени скорости реакции с самоускорением 1. Автокаталитические реакции, в которых один из продуктов реакции ускоряет процесс. Пока этого продукта мало, реакция медленная. Накопление катализатора ведет к ускорению реакции до тех пор, пока в конце процесса убыль исходных веществ не обусловит снижение скорости. 2. Биохимические реакции, вызываемые микроорганизмами – брожение, ферментация. На начальной стадии процесса его скорость возрастает в связи с интенсивным размножением микроорганизмов. В конце процесс замедляется вследствие недостатка «пищи». 3. Автотермические процессы, в которых вначале за счет тепла экзотермической реакции происходит разогрев, ведущий к росту скорости. 4. Процессы кристаллизации. В начальной стадии процесса скорость растет благодаря увеличению числа зародышей кристаллизации. Затем образование новых зародышей прекращается и скорость снижается из-за уменьшения пересыщения. Если процесс такого типа проводить в аппарате вытеснения, то на начальном отрезке аппарата скорость реакции мала и эта его часть используется неэффективно. В таком случае более эффективным может оказаться аппарат смешения: в нем несложно поддерживать высокую концентрацию катализатора, микроорганизмов, зародышей кристаллизации или высокую температуру. Причем эта оптимальная концентрация или температура поддерживается во всем объеме аппарата. После того как процесс пройдет через максимум скорости, он будет идти как процесс с падающей скоростью. Поэтому на этом этапе (на «хвосте» процесса) смесь выгодно вывести из аппарата смешения и направить в аппарат вытеснения. В ряде подобных случаев процесс можно проводить и в аппарате вытеснения, но тогда для ускорения начальной стадии процесса осуществляют циркуляцию: часть потока, выходящего из аппарата, возвращают на его вход (рис. 4.7). С этим циркуляционным потоком в начальный участок аппарата вносится «затравка», ускоряющая процесс. Можно отметить, что циркуляцию вообще можно рассматривать как один из механизмов продольного перемешивания. Естественно, если агент, ускоряющий процесс, – это тепло, то не нужно смешивать входящий и циркулирующий потоки, тепло от уходящей жидкости ко входящей может быть передано через стенку. Сложные реакции в идеальных потоках: селективность. Потеря селективности для последовательных реакций в ИС. Параллельные реакции одинакового порядка – независимость селективности от потока. Дифференциальная селективность. Разные порядки. Средняя селективность – это интегральная селективность. Сложные реакции в идеальных аппаратах. При проведении сложных реакций с побочными стадиями обычно главной задачей является достижение высокой селективности. Зачастую ради этого жертвуют степенью превращения: недопревратившиеся реагенты можно отделить от вышедшей из аппарата смеси и вернуть в начало процесса. В результате стоимость переработки возрастает на величину стоимости процесса разделения. Низкая же селективность означает, что, во-первых, часть исходных веществ затрачивается бесполезно (переходит в ненужные побочные продукты); во-вторых, эти побочные продукты также приходится отделять (затраты на разделение могут быть даже большими, чем при низкой степени превращения); в-третьих, с побочными продуктами после их отделения нужно что-то делать. Просто выбросить их, как правило, нельзя: загрязнение окружающей среды в наше время становится одной из тяжелейших проблем, стоящих перед человечеством. Обезвреживание или уничтожение побочных продуктов ложится тяжелым грузом на экономику процесса. Характер влияния структуры потока на протекание сложных реакций отличается большим разнообразием. \ Рассмотрим два простых случая: реакцию с последовательной побочной стадией и реакцию с параллельной побочной стадией. Для последовательной побочной стадии вначале проведем качественный анализ. Реакция А → В → С, где В – целевой продукт, а С – побочный. На качественном этапе кинетические порядки стадий несущественны. Построим график, аналогичный приведенному на рис. 4.5 (изменение концентрации по длине аппарата), но по оси ординат отложим изменение концентрации целевого продукта В (рис. 4.8). По оси абсцисс по-прежнему – координата длины от входа к выходу. Рис. 4.8. Изменение концентрации целевого продукта по длине аппарата: 1 – идеальное вытеснение, 2 – идеальное смешение Учтем, что скорость второй (побочной) реакции тем выше, чем больше концентрация В. Изменение показателей процесса по длине в аппарате вытеснения такое же, как изменение по времени в периодическом процессе, проанализированное в конце разд. 3.2 (см. табл. 3.2). Вначале концентрация В мала, а концентрация А велика; скорость образования В – большая, а скорость побочной реакции – маленькая. Селективность при этом близка к 1. Затем, по мере исчерпания А и накопления В, скорость первой стадии снижается, скорость второй растет и селективность уменьшается. В аппарате же смешения по всей длине мала концентрация реагента А и велика концентрация В. Во всем объеме аппарата процесс протекает с минимальной селективностью. Если обе стадии 1-го порядка, то, Для параллельной реакции (В – целевой продукт) А→В А→С влияние структуры потока на селективность зависит от соотношения порядков основной и побочной стадий. Аналитические выражения для σ не всегда достаточно просты, поэтому легче провести анализ на основе другой характеристики – отношения скоростей образования обоих продуктов: Величина ω не равна σ, но симбатна ей: чем больше отношение скоростей, тем больше селективность. Если обе стадии одинакового порядка, то ω зависит только от соотношения констант скоростей обеих стадий: В этом случае селективноcть не меняется по ходу реакции (если температура постоянна) и не зависит от характера потока. Если же порядки разные (n1 и n2), то Теперь селективность зависит от концентрации А. Например, если целевая (первая) реакция 1-го порядка, а побочная – 2-го, то ω обратно пропорциональна сА. Обратимся к рис. 4.5. При заданной степени превращения А его концентрация в любом поперечном сечении аппарата смешения будет ниже, чем в соответствующем сечении аппарата вытеснения. Значит, в случае, когда n1< n2, процесс в аппарате идеального смешения будет проходить хотя и медленнее, но зато с существенно большей селективностью, т. е. именно аппарат смешения окажется наилучшим. Нетрудно понять, что если целевая реакция 2-го порядка, а побочная – 1-го, то все преимущества будут у аппарата вытеснения. Время пребывания в потоке. Простой метод исследования и диагностики, но полезный только при 1 кинетическом порядке. Имеются условия (в первую очередь связанные с необходимостью получения высокой степени превращения), когда продольное перемешивание сильно ухудшает показатели процесса. В этих случаях имеет место не только резкое различие в эффективностях аппаратов идеального вытеснения и идеального смешения, но и заметное влияние небольших отклонений от идеального вытеснения. Даже в аппаратах со слабыми отклонениями от равномерности времени пребывания процесс идет не так, как при идеальной модели. Наблюдаются и такие случаи, когда аппарат (или участок аппарата), в котором создается интенсивное перемешивание, не описывается с достаточной точностью моделью идеального смешения. При всей привлекательности самого исчерпывающего подхода – изучения поля скоростей, он слишком сложен. В ряде случаев его использование дает важные результаты, но часто желательно воспользоваться более простым методом. Для этого может служить исследование распределения времени пребывания жидкости в аппарате. Правда, при таком подходе многое теряется; например, мы не узнаем, каковы скорости в разных частях аппарата. Действительно, рассмотрим рис. 4.10. На нем схематически изображены эпюры скорости в поперечных сечениях трех аппаратов. В одном аппарате профиль скоростей – парабола с максимумом на оси потока, в другом – поток идет в основном вдоль левой стенки, в последнем – поток в среднем равномерен по сечению, но из-за турбулентных пульсаций одни его частицы обгоняют другие. Однако с той точки зрения, которую мы сейчас излагаем, эти аппараты неотличимы один от другого. Каждый из них часть жидкости проходит быстрее, чем поток в среднем, часть – медленнее. Если для двух аппаратов эти части одинаковы, то и потоки представляются одинаковыми. Таким образом, мы обедняем картину потока, исключая много важных подробностей. Рис. 4.10. Эпюры скоростей при неравномерности трех видов: а – симметричной; б – несимметричной; в – хаотичной При этом мы получаем серьезные преимущества. Во-первых, эксперимент при таком подходе прост. Во-вторых, данные опытов легко поддаются количественной обработке и трактовке: из всех переменных остается одна – время пребывания. В-третьих, полученные результаты достаточны для многих случаев. В-четвертых, если этих данных окажется недостаточно для анализа процесса, то в дальнейшем можно перейти к снятию поля скоростей. При этом информация о распределении времени пребывания поможет наилучшим образом спланировать соответствующий эксперимент и упростить обработку его результатов. Наша цель – узнать, какое количество текущей жидкости будет находиться в аппарате в то или иное время. Отдельные частицы неразличимы, поэтому, чтобы различить их, выделим из всей совокупности те из них, которые вошли в аппарат в некоторый зафиксированный момент и примем его за начало опыта. Таким образом, выделенные частицы образуют представительную выборку из генеральной совокупности частиц, движущихся через аппарат. Для выделения интересующих нас частиц пометим жидкость, входящую в аппарат в момент, который примем за начало опыта (t= 0). С этой целью во входящий поток быстро добавляем порцию какой-либо примеси, называемой индикатором, или трассером. Индикатор должен быть легко количественно определим. Кроме того, его добавление не должно влиять на характер потока (в частности, его следует вводить мало, чтобы существенно не изменять расход), а сам он должен двигаться вместе с потоком, ни с чем не реагируя и не сорбируясь. Начиная с момента t = 0 на выходе из аппарата измеряют концентрацию индикатора си как функцию t. Типичный график зависимости си (t) показан на рис. 4.11. В момент t = 0 на входе резким импульсом вводится индикатор (рис. 4.11,а). При мгновенной подаче конечного количества индикатора его концентрация будет бесконечной. Реально получается более или менее узкий и высокий импульс. На выходе (рис. 4.11, б) вначале си= 0: ни одна частица индикатора не успела дойти до выхода. В момент t 1 выхода достигает самая быстрая часть потока, появляется индикатор. Далее его концентрация нарастает до момента t 2 , а затем начинает убывать: основная масса потока прошла, выходят те части индикатора, которые попали в зоны циркуляции или застоя. Выход этих порций обычно продолжается долго; лишь через большой промежуток времени практически весь индикатор покидает аппарат. Обозначим количество индикатора, находящееся в данный момент в аппарате, через gи. В начальный момент в аппарате находилось все введенное в поток количество индикатора gи0. Концентрацию индикатора на выходе обозначим через си. Рассмотрим произвольный текущий момент. За единицу времени из аппарата выйдет объем жидкости, равный расходу v; за бесконечно малый промежуток dt, отсчитываемый от данного момента, – объем vdt. Количество индикатора, вышедшего из аппарата за промежуток dt, составит Знак «–» означает, что количество индикатора убывает, т.е. индикатор уходит из аппарата. Дальнейший анализ целесообразно вести, перейдя к безразмерным величинам. В эксперименте си тем больше, чем больше введенное количество индикатора gи0. Но при изучении потока величина gи0 – несущественная, она определяется случайными обстоятельствами опыта. Безразмерная концентрация не должна от нее зависеть. Переходим к безразмерным единицам: Для каждой величины u на исследуемом объекте выберем характерное значение u0 . v=u/u0 Безразмерные величины С и τ имеют тот же физический смысл концентрации и времени, что и размерные. Изменились лишь масштабы, в которых они измеряются. Преобразуем уравнение (4.46), используя сначала формулы (4.51) и (4.52), а затем (4.47) и (4.48) и вынося постоянную величину t за знак дифференциала: Доля от общего количества проходящей через аппарат жидкости, равная Сdτ, имеет время пребывания τ с точностью до dτ. Безразмерная концентрация индикатоpa С равна плотности вероятности (дифференциальной функции распределения) времени τ как случайной величины. Для функции С(τ) (функция С) верны все свойства, выраженные формулами (2.3) – (2.5), с некоторыми уточнениями, связанными со следующей особенностью: С = 0 при τ < 0 (4.54) Смысл формулы (4.54) таков: вероятность того, что частица выйдет из аппарата раньше, чем войдет в него, равна нулю. Поэтому в интегралах (2.4) и (2.5) нижний предел можно заменить на 0. При импульсной подаче индикатора на выходе имеем C(τ). Чтобы получить F(τ), характер подачи (сигнал на входе) должен быть иным: до момента τ = 0 концентрация индикатора равна нулю; в этот момент (теоретически мгновенно) концентрация скачком возрастает до 1 и далее остается на этом уровне (рис. 4.12,а). Некоторые другие величины, характеризующие пребывание в потоке Среднее время пребывания. Размерный вид формулы: Рассчитав t по формуле, можно решить одну из двух задач: либо по известному Va рассчитать расход жидкости, либо по известному v – неизвестный объем. Дисперсия времени пребывания По размерным значениям расчет можно вести, пользуясь формулой Распределение времени пребывания и степень превращения. В случае изотермической необратимой реакции 1-го порядка степень превращения однозначно определяется константой скорости, средним временем пребывания и видом дифференциальной функции распределения. Такая же однозначность имеет место при протекании обратимой реакции и любой сложной реакции, все стадии которой проходят по первому порядку. Уравнения тепло- и массопередачи аналогичны уравнению обратимой химической реакции 1-го порядка, поэтому подчиняются аналогичным закономерностям: где Kт – коэффициент теплопередачи; T1 и T2 – температуры теплоносителей. Для реакций не 1-го порядка приходится учитывать ряд дополнительных факторов. Но во многих случаях первоначальную оценку влияния потока можно получить и для них, имея данные о распределении времени пребывания. Законы распределения времени пребывания для идеальных потоков Рассмотрим, какой вид имеют дифференциальная и интегральная функции распределения для аппарата идеального вытеснения. Так как время пребывания всех частиц одинаково, то при τ < 1 выхода не достигнет ни одна меченая частица: С = 0. При τ > 1 также С = 0: все меченые частицы уже прошли. Функция С(τ) отлична от нуля лишь при τ = 1. Но по условию (4.67) Если функция отлична от нуля только в одной точке, а площадь под ее кривой конечна, то в этой точке функции придется приписать бесконечное значение единица в скобках – это значение времени, при котором происходит бесконечный импульс. Изобразить график δ-функции невозможно; график С(τ) для некоего режима, близкого к идеальному вытеснению, показан на рис. 4.13. Это весьма узкий, крутой и высокий пик. Интегральная функция для данного случая показана на рис. 4.14. Функция F(τ) = 0 при τ < 1. При τ= 1 происходит ее скачок, и при 1 < τ < +∞ функция F(τ) = 1: из аппарата уже вышла вся жидкость, вошедшая в него в момент τ= 0. Для получения на выходе функции С(τ) необходимо подать индикатор на вход по закону δ-функции (см. рис. 4.11,а). Если на выходе желательно получить F(τ), сигнал на входе должен быть интегралом от δ-функции (см. рис. 4.12,а). В потоке идеального вытеснения входной сигнал, не искажаясь, переносится от входа к выходу за время τ= 1. Выходной сигнал, соответственно С(τ) или F(τ), совпадает по форме с входным, но сдвинут по оси абсцисс на единицу. Основное свойство δ-функции выглядит так. Для любой функции φ(τ) справедливо равенство Функция С(τ) для потока идеального смешения. Результат тот же, что и полученный на базе иных соображений (из рассмотрения материального баланса). Рассмотрим протекание необратимой реакции 2-го порядка А → В в потоке, характеризуемом дифференциальной функцией распределения времени пребывания С(τ). Сегрегация и перемешивание. Точность при других порядках. Примеры функций распределения по времени пребывания, их получения. Уровни перемешивания. Сегрегация. Итак, двумя способами мы получили два разных выражения для реакции 2-го порядка, проходящей в потоке идеального смешения: (4.42) из материального баланса и (4.84) из распределения времени пребывания. Расчет χ по обеим формулам графически представлен на рис. 4.16. Рис. 4.16. Степень превращения для реакции 2-го порядка в аппарате смешения: 1 – по формуле (4.84); 2 – по формуле (4.42) При больших значениях χ различие между результатами двух расчетов весьма существенно. Горизонтали на графике показывают: в соответствии с уравнением (4.84) для достижения χ = 0,8 нужен аппарат вдвое меньшего объема, чем рассчитанный по уравнению (4.42); если же нужно обеспечить χ = 0,925, то эта разница достигнет 3,7 крат. Какое же уравнение правильно? В каком выводе допущена ошибка и какая? «Сортируя» жидкость, вытекающую из аппарата, по времени пребывания, мы предполагали, что каждая частица проходит аппарат сама по себе. На деле же частицы взаимно смешиваются. Это смешение не влияет на ход реакции 1-го порядка: в ней каждая молекула реагирует независимо от того, какие молекулы ее окружают. Но в реакции 2-го порядка (и любого другого, кроме нулевого и 1-го) вероятность вступления молекулы в реакцию зависит от вероятности ее столкновения с другими молекулами. А эта вероятность зависит от концентрации и изменяется при смешении частиц. Однако было бы слишком поспешно заключить из сказанного, что при расчете по формуле (4.84) результат всегда неверный, а при расчете по (4.42) всегда верный. Дело в том, что в реальных случаях отдельные частицы смешиваются одна с другой в разной степени. По определению, в аппарате идеального смешения каждая входящая частица полностью перемешивается со всеми другими и составляющие ее молекулы равномерно рассеиваются по всему аппарату (рис. 4.17, а). При этом формула (4.42) будет верной. Но возможен и иной случай. Представим себе другой (также идеализированный) характер движения. Входящие в аппарат частицы жидкости мгновенно равномерно распределяются по его объему : с этой точки зрения в аппарате наблюдается идеальное смешение. Но каждая частица движется в потоке как единое целое, не перемешиваясь с окружающими частицами. Поэтому хотя в среднем концентрация вещества во всех частях аппарата одинакова, однако если рассмотреть маленький его участок в увеличенном масштабе (рис. 4.17, б), то станет видно, что эта средняя концентрация складывается из значений, хаотически колеблющихся от частицы к частице. В первом случае говорят об идеальном смешении на микроуровне, во втором – об идеальном смешении на макроуровне при полной сегрегации (разделении) на микроуровне. Итак, для расчета протекания реакции 1-го порядка достаточно знать дифференциальную функцию распределения времени пребывания. Для реакций более высоких (а также и более низких) порядков этого уже недостаточно, так как начинает сказываться ограниченность подхода, не учитывающего особенности перемешивания в аппарате. Понятие о сегрегации – один из путей преодоления этой ограниченности. К сожалению, строгих количественных характеристик для случаев, промежуточных между полным смешением на микроуровне (сегрегация равна нулю) и полной сегрегацией (равной единице), видимо, пока не имеется. Можно говорить лишь о большей или меньшей сегрегации. В случае идеального вытеснения, если за частицу принимать малый движущийся объем, занимающий все поперечное сечение, сегрегация всегда полная: такие частицы в этом потоке между собой не перемешиваются. В потоках смешения в принципе возможны ситуации с любой степенью сегрегации. Если нет оговорки, то поток считают несегрегированным. При гомогенных, не слишком быстрых реакциях в турбулентных потоках степень сегрегации близка к нулю. Повышение вязкости и переход в ламинарный режим увеличивают сегрегацию. Рис. 4.17. Изменение концентрации по длине в увеличенном масштабе: а – идеальное смешение на микроуровне; б – полное смешение на макроуровне при полной сегрегации Высокой может быть сегрегация в случае очень быстрых реакций: за время их протекания частицы не успевают перемешаться. В дисперсных фазах многофазных потоков сегрегация может быть близка к единице. Так, если реакция идет в твердых частицах, проходящих через аппарат (например, в псевдоожиженном слое), то сегрегацию можно считать полной. Сегрегация дисперсной фазы эмульсии или пены зависит от того, насколько часто сливаются (коалесцируют) капли или пузыри. Ход реакции не 1-го порядка зависит не только от степени сегрегации, но и от иных особенностей потока. Так, если в аппарате чередуются зоны с разным характером потока, то степень превращения зависит от порядка чередования этих зон. Пример 4.10. Рассмотрим протекание необратимой реакции А → В в двух системах последовательно соединенных и равных по объему аппаратов идеального смешения и идеального вытеснения. В первой системе вначале включен аппарат вытеснения, а во второй– аппарат смешения. Среднее время пребывания в каждом аппарате – 1 мин. Концентрация реагента на входе – 1 кмоль/м3. Расчет проведем для двух случаев: 1) реакция 1-го порядка, k = 1 мин-1; 2) реакция 2-го порядка; k = 1 м3/(кмоль·мин). Для реакции 1-го порядка и первой системы концентрация вещества А после первого аппарата определяется по формуле 4. Модели неидеальных потоков Параметры моделей. Неидеальное через идеальное как метод моделирования неидеальных потоков. Параметры модели. Чаще всего простота или сложность математической модели связаны с тем, сколько в нее входит параметров – коэффициентов, учитывающих те или иные особенности объекта. Значения параметров характеризуют свойства данного конкретного объекта, отличающие его от других объектов того же класса. Чем больше параметров входит в модель, тем подробнее удается охарактеризовать его и тем точнее описать. На одном полюсе здесь выступают предельно идеализированные модели, такие, как идеальный газ, абсолютно упругое тело и др. Уравнения при этом либо вообще не содержат параметров, включая лишь универсальные константы (идеальный газ), либо их число минимальное (модуль упругости в законе Гука). Эти идеализированные модели почти полностью игнорируют конкретные свойства объектов. На другом полюсе — сложные многопараметрические модели, учитывающие много конкретных свойств. Так как мы всегда хотим иметь максимально точное описание объекта, с этой точки зрения сложные модели обладают несомненными преимуществами. Но у сложных моделей есть и недостатки. Прежде всего такую модель трудно обрабатывать. Если данная модель входит как составная часть в сложные модели более высоких иерархических уровней, то в конце концов может получиться такое громоздкое описание, что его не удастся обсчитать. К тому же, чем сложнее зависимость, тем труднее представить себе, как она выглядит в целом. Хотя такая наглядность, возможность составить общее представление о характере зависимости не обязательно нужна при моделировании, но обычно она заметно облегчает анализ. Еще одна трудность, связанная с применением многопараметрических моделей, — это чувствительность к ошибкам опытов. Чем больше параметров, тем более точный эксперимент требуется, чтобы достаточно хорошо оценить эти параметры. Если модель построена на основе структурного подхода, а эксперимент не очень точен, то возникает специфическая опасность потери физического смысла: можно получить неверные значения параметров, хотя модель в целом будет давать приемлемое совпадение с опытными данными. Это происходит потому, что ошибки в значениях разных параметров взаимно компенсируются. Модель остается пригодной для количественного описания объекта (в достаточно узких пределах), но физический смысл искажается — мы получаем превратное представление о величинах эффектов, связанных с параметрами. В конце концов физический смысл теряется и параметры модели получают смысл подгоночных параметров, назначение которых — лишь привести в соответствие данные и модель. Уравнение становится эмпирическим, о чем исследователь может не знать. Проиллюстрировать это можно даже на примере достаточно простого двухпараметрического уравнения Ван-дер-Ваальса. Простейшие модели. Ячеечная модель. Ячеечная модель – простейшая однопараметрическая модель. Эта модель схематически представляет реальный аппарат как некоторое число п одинаковых последовательно соединенных аппаратов (ячеек) идеального смешения (рис. 4.18). Суммарный объем всех ячеек равен объему реального аппарата, следовательно, объем каждой ячейки равен Va/n (Общий объем поделен на n (один параметр) равных последовательных объемов ИС.) Число ячеек – единственный параметр ячеечной модели. В ряде случаев в аппарате действительно можно выделить участки по ходу потока, в каждом из которых жидкость более или менее полно перемешивается. Системы, близкие к ячеечной модели. Схема ячеечной модели близка, например, к картине движения жидкости через каскад реакторов с мешалками или через тарельчатую барботажную колонну провального типа, в которой жидкость интенсивно перемешивается на каждой тарелке и быстро переливается с тарелки на тарелку. В других потоках отождествить физическую картину с ячеечной моделью можно лишь ценой значительных упрощений. Например, для турбулентного потока в первом приближении можно считать, что каждая частица проходит некоторое расстояние как единое целое, а затем перемешивается с окружающим частицами. Участок, на котором происходит это перемешивание (путь смешения), можно, хотя и весьма грубо, сопоставить с ячейкой смешения. Другой такой пример – течение газа в зернистом слое. Выходя из узкой щели между зернами в более широкую полость (такие всегда есть в слое), газ завихряется и перемешивается, в результате чего возникает картина чередующихся перетеканий и перемешиваний. Но и здесь схема ячеечной модели сильно огрубляет реальное явление. Однако в ряде случаев ошибка огрубления несущественна для решения конкретной задачи, а простота модели делает ее применение желательным Дифференциальная функция распределения по временам пребывания ДФРВП вида C()=nnn-1e-n/(n-1)!. n=1, n=∞. 2()=1/n как оценка n. Поведение при n=∞!!! Концентрация реагента от времени пребывания для ИВ, ИС и ЯМ (n=3). Выход i-1 как вход i. n уравнений. Решать последовательно. Для конечной концентрации реагента реакции первого порядка CAn=CA0/(1+kt/n)n Рассмотрим распределение времени пребывания и изменение концентрации по длине аппарата для ячеечной модели. Дифференциальная функция распределения времени пребывания имеет вид (формула приводится без вывода) График этой функции изображен на рис. 4.19. По мере увеличения числа ячеек кривые становятся все более крутыми, приближаясь к графику δ-функции. При п = 1 формула (4.85) переходит в уравнение (4.78), при п→∞ – в (4.74). Таким образом, потоки идеального смешения и идеального вытеснения являются крайними случаями ячеечной модели. а Разумеется, физическая схема, включающая 0,77 ячейки смешения, не имеет смысла. Приходится полагать, что параметр n содержит эмпирическую поправку. Впрочем, и в тех случаях, когда число ячеек связано с совершенно определенным числом конструктивных элементов (например, тарелок колонны), эксперимент по изучению распределения времени пребывания, как правило, дает значение n, отличное от этого числа и чаще всего не целое. Различие объясняется отклонением течения на каждой ступени от идеального, а также случайными ошибками эксперимента. Поэтому n и здесь содержит эмпирическую поправку. В некоторых расчетах удается использовать нецелое n, в других – параметр округляют. Распределение концентрации реагента по длине аппарата показано на рис. 4.20. Для последней ячейки концентрация вещества А в ячеечной модели совпадает с его концентрацией при идеальном смешении. Но первые ячейки работают при бóльших сА и соответственно при бóльших скоростях реакции. С этой точки зрения ячеечная модель занимает промежуточное место между обеими моделями идеальных потоков. Рис. 4.20. Распределение концентрации реагента по длине аппарата: 1 – идеального вытеснения; 2 – идеального смешения; 3 – состоящего из трех ячеек. Рис. 4.21. Схема аппарата из трех ячеек. Рассмотрим теперь протекание химической реакции в ячеечной модели. Описание этого процесса есть просто описание процесса при идеальном смешении, повторенное n раз. Выходные значения концентрации и температуры i-й ячейки являются входными для (I + 1)-й. Для реакции А → В это показано на рис. 4.21. Для i-й ячейки уравнение баланса по веществу J в стационарном режиме имеет вид Для конверсии =1-1/(1+kt/n)n. Среднее время! Крайние случаи. Дробное n. Секционирование, перегородки. Пример 4.11 показывает, что с увеличением числа ячеек степень превращения довольно быстро приближается к результатам, характерным для идеального вытеснения. Ясно, почему в технологии часто применяется прием секционирования: аппараты, в которых создается интенсивное смешение потока жидкости, делят на последовательные секции, между которыми она перетекает по возможности без смешения. Для этого обычно служат всякого рода перфорированные перегородки. Иногда для достижения того же эффекта применяют каскады последовательно соединенных аппаратов с мешалками. Кроме увеличения степени превращения секционирование влияет и на другие показатели процесса, в частности на селективность. Селективность. Уже три ячейки эффективны! Особо – при порядке 0! Таким образом, и в этом случае несомненна целесообразность секционирования аппарата: растет как степень превращения, так и селективность. Динамика, чувствительность, управляемость, устойчивость. Параметрическая чувствительность и управляемость. Разница и сходство. Процессы в динамике (меняющиеся во времени) также играют в химической технологии большую роль. К ним относятся все периодические процессы, а также такие важные этапы любого процесса, как пуск и остановка, и переходные процессы, возникающие при изменениях режима работы вследствие либо случайных возмущений, либо регулирующих воздействий. Математическое описание нестационарного процесса обязательно содержит производные по времени. В простейшем случае это связано с членами, описывающими накопление. Поэтому математический аппарат, применяемый для описания и анализа этих процессов, – дифференциальные уравнения. Методы анализа результатов на основе дифференциальных уравнений, например метод Лапласа [13]. Рассмотрим простейшие случаи – переходные процессы в идеальных аппаратах при ступенчатом возмущении по концентрации. Такой тип возмущения часто анализируется в теории: до некоторого момента t = 0 величина на входе имела одно значение, а затем мгновенным скачком принимает новое значение, которое сохраняется в дальнейшем. Пример подобного возмущения (по концентрации индикатора) показан на рис. 4.12,а. Рассмотрим протекание необратимой реакции 1-го порядка А → В в аппарате идеального смешения. Температура и расход жидкости постоянны. До момента t = 0 концентрация вещества А на входе составляла c01, затем она скачком возросла до c02. Математическое описание процесса состоит из одного уравнения баланса, являющегося частным случаем уравнения (4.34): Это и есть уравнение нашего переходного процесса, которое описывает изменение концентрации на выходе из аппарата, графически показанное на рис. 6.1,б. Рис. 6.1. График переходного процесса в аппарате идеального смешения: а – на входе; б – на выходе График – экспонента, начинающаяся от первого стационарного значения и асимптотически приближающаяся ко второму. Объект, описываемый уравнением (6.1) или соответственно (6.4), в теории автоматического регулирования называют апериодическим звеном 1-го порядка. Постоянная времени в данном случае составляет . По-иному выглядит переходный процесс в аппарате идеального вытеснения. В стационарном режиме при cA0 = c01 концентрация вещества А на выходе аппарата определяется формулой (4.14): Если на входе происходит возмущение, то вначале оно никак не проявляется на выходе – те порции жидкости, в которых начальная концентрация изменилась, до выхода еще не дошли. Когда же пройдет время, равное t , концентрация скачком изменится до (рис. 6.2). Рис. 6.2. График переходного процесса в аппарате идеального вытеснения: 1 – на входе; 2 – на выходе С точки зрения теории автоматического регулирования в аппарате идеального вытеснения имеет место чистое запаздывание (транспортное запаздывание). В ряде случаев анализ математической модели позволяет обнаружить такие особенности процесса, предсказание которых по лабораторным данным невозможно или весьма затруднительно, поскольку они сильно зависят от размеров объекта. Рассмотрим две такие особенности. Параметрическая чувствительность Пij – производная от i-й выходной величины по j-му входному параметру: Чем больше Пij , тем сильнее влияет данный фактор на выход. Если параметрическая чувствительность очень мала, то соответствующим фактором нельзя пользоваться как управляющим: он почти не влияет на процесс. Если параметрическая чувствительность чрезмерно велика, процесс становится трудноуправляемым. Даже малые колебания входного параметра приводят к резким колебаниям режима. Поэтому приходится либо чрезвычайно точно стабилизировать вход, либо тем или иным способом снижать чувствительность. Отмечу, что поскольку Пij — функция входных факторов, то при их изменении процесс может попадать в области и малой, и высокой чувствительности. Пример 6.1. Рассчитано протекание необратимой экзотермической реакции 1-го порядка А → В в аппарате идеального вытеснения с охлаждаемой стенкой [38]. Исследовано влияние температуры стенки Тп (постоянной по длине аппарата) на температуру в горячей точке – наибольшую температуру в зоне реакции. Математической моделью процесса являются уравнения (4.5), (3.53) и (5.28). Результаты моделирования показаны на рис. 6.3. Рис. 6.3. График чувствительности трубчатого реактора к температуре стенки По оси абсцисс отложено время реакции (начиная от момента входа смеси в аппарат), по оси ординат – температура смеси. До Тп = 335 К параметрическая чувствительность невелика. Это объясняется тем, что входящая смесь охлаждается и реакция идет очень медленно. Но затем при росте Тп начинается бурное развитие реакции, самоускоряющейся за счет выделения тепла. Увеличение Тп на 2,5 К (от 335 до 337,5 К) вызывает рост температуры в горячей точке почти на 70 К. Отсюда находим, что П ≈ 70 : 2,5 = 28. Если в рассмотренном случае использовать изменяющуюся по длине температуру стенки (вначале значение Тп относительно велико, а затем оно снижается), то скачок температуры сгладится и П понизится. Управлять процессом будет легче. Заметим, что в ряде случаев параметрическую чувствительность целесообразно определять так, как это сделано в примере 6.1: заменяя в уравнении (6.5) производную отношением малых конечных приращений Предельный случай параметрической чувствительности: П → ∞. Это означает, что бесконечно малое изменение входного параметра вызывает конечное изменение показателей работы. Такая ситуация наблюдается при неустойчивости процессов. Флуктуации и возмущающие воздействия. Связь. Устойчивость стационарных режимов в ХТ. Устойчивость химических процессов определяется их реакцией на возмущающие воздействия. Если процесс, проходящий устойчиво, отклонить от данного состояния, а затем предоставить самому себе, то он самопроизвольно вернется в начальное состояние. Наиболее известно явление устойчивости равновесия механических систем. Так, стул, стоящий на четырех ножках, устойчив. Если его слегка наклонить, а затем отпустить, то он вновь станет на ножки. Устойчив также стул, лежащий на боку. Теоретически можно уравновесить стул и на двух ножках, и даже на одной. И если бы он не испытывал никаких толчков, то простоял бы в таком положении неопределенно долго. Но достаточно легкой вибрации пола – и стул, отклонившись от положения равновесия, уже не вернется к нему, а будет отклоняться дальше, пока не встанет на четыре ножки или не упадет на бок. Равновесие стула, стоящего на одной или двух ножках, неустойчиво. Если систему, находящуюся в неустойчивом равновесии, вывести из него, а затем предоставить самой себе, то она будет самопроизвольно продолжать отклоняться от исходного состояния. Вопрос о том, что может произойти с ней дальше, я вкратце рассмотрю немного ниже. Из примера со стулом ясно, что одна из возможностей (возникающая, пожалуй, чаще всего) – приход к какому-либо устойчивому равновесию. В химической технологии обычно анализируют устойчивость стационарных режимов работы. В любом технологическом процессе стационарный режим подвержен случайным колебаниям (возмущениям). Предположим, что в результате возмущения значение какогото входного параметра х, влияющего на работу аппарата, слегка отклонилось от постоянной величины (рис. 6.4,а) и затем вернулось к начальному положению. Как будет вести себя аппарат, находящийся в устойчивом и в неустойчивом состояниях? О работе аппарата будем судить по изменению во времени значения какого-либо из выходов системы у. Если исходный режим устойчив, то переходный процесс будет проходить приблизительно так, как показано на рис. 6.4,б, – через некоторое время после снятия возмущения режим вернется к начальному состоянию. Если же состояние аппарата было неустойчивым, то при том же характере возмущения по окончании переходного процесса аппарат окажется уже в каком-либо другом, устойчивом состоянии (рис. 6.4,в). Рис. 6.4. Графики возмущающего воздействия (а) и переходных процессов при устойчивом (б) и неустойчивом (в) режимах Необратимая экзотермическая реакция первого порядка в потоке ИС с отводом тепла. Скорость r=kCA0/(1+kt)=Ae-E/RTCA0/(1+Ae-E/RTt). При низкой т-ре Ae-E/RTCA0, при высокой CA0/t (смысл!). Рассмотрим задачу об устойчивости химических процессов на примере тепловой устойчивости экзотермической необратимой реакции 1-го порядка, протекающей в аппарате идеального смешения с отводом тепла. Для анализа этого случая нам потребуется зависимость скорости реакции, протекающей в аппарате идеального смешения, от температуры. Поэтому вначале найдем эту зависимость. Имеем необратимую реакцию 1-го порядка А → В, протекающую в аппарате идеального смешения. Скорость реакции выражается формулой Рис. 6.5. Температурная зависимость скорости реакции в аппарате идеального смешения Вначале зависимость (6.8) может показаться парадоксальной. Почему скорость реакции зависит не от концентрации в зоне реакции (которая при высокой температуре очень мала), а от концентрации реагента на входе в аппарат? Почему на скорость влияет среднее время пребывания? Учет особенностей процесса делает, однако, физический смысл такой зависимости достаточно ясным. При высоких температурах реакция протекает быстро, поэтому перерабатывается практически все вещество, вводимое в аппарат. Скорость реакции определяется просто количеством реагента, вводимого в аппарат в единицу времени (отсюда множитель cA0 в числителе формулы (6.8)), а также средним временем, затрачиваемым на переработку. Для анализа важно то, что в этом режиме скорость r не зависит от температуры: с ростом Т увеличивается k и одновременно уменьшается сА, но так как концентрация А на выходе очень мала, ее дальнейшее уменьшение практически не сказывается на разности (сА0 – сА) и соответственно на скорости реакции. Теперь перейдем к анализу устойчивости данной реакции. Реакция протекает в аппарате идеального смешения. Тепло реакции отводится через поверхность Fт к теплоносителю, имеющему температуру Tтн. Баланс Q1=Q2, где 1 от реакции, 2 отвод потоком и стенкой. VaQpr=vCT(TT0)+KTFT(T-TTH). Перегруппировка. Вид функций. Максимально 3 корня, 3 стационарных состояния. Возмущение температуры. Устойчивость 1 и 3. Если процесс стационарен, то его характеризует уравнение теплового баланса, которое запишем в виде Обозначим левую часть уравнения через Q1, а правую – через Q2. Здесь Q1 – выделение тепла, т. е. количество тепла, выделяемого реакцией в единицу времени; Q2 – отвод тепла, т. е. количество тепла, выводимого в единицу времени с потоком и через стенку (за вычетом входящего с потоком). Итак, в стационарном режиме Q1 = Q2. (6.10) Если Q1 ≠ Q2, процесс нестационарен: при Q1 > Q2 температура растет во времени – система нагревается; при Q1 < Q2 система охлаждается. Исследуем, как зависят левая и правая части уравнений (6.9) – (6.10) от температуры в аппарате. В левой части VaQp – коэффициент, почти не зависящий от Т, так что функция Q1(Т) имеет такой же вид, как функция r (Т), изображенная на рис. 6.5, отличаясь лишь постоянным множителем. Правую часть уравнения (6.9) преобразуем, выделив скобками величины, не зависящие или почти не зависящие от T: Таким образом, это практически линейная зависимость, причем Q2 растет с повышением Т. На рис. 6.9 зависимости Q1 и Q2 от Т представлены графически. Линия I выделения тепла и линия II отвода тепла пересекаются в трех точках 1, 2 и 3 при температурах Т1, Т2 и T3. При этих температурах соблюдается условие (6.10) и процесс стационарен. Итак, в данной ситуации при одних и тех же значениях всех внешних (входных) параметров возможны три различных стационарных режима. Рассмотрим вначале стационарный режим при температуре Т1. Так как скорости выделения и отвода тепла равны одна другой, то пока температура не меняется, режим остается стационарным. Предположим теперь, что в результате случайного возмущения температура в реакторе немного повысилась и стала равной T1 + dT (рис. 6.6). При этом из-за ускорения реакции возрастает скорость выделения тепла; этот рост происходит в соответствии с кривой тепловыделения. Одновременно из-за увеличения разности температур между реактором Рис. 6.6. Зависимости выделения и отвода тепла от температуры в реакторе и теплоносителем повышается скорость отвода тепла. Этот рост характеризуется прямой теплоотвода. В точке 1 прямая идет круче кривой, поэтому при температуре T1 + dT скорость отвода тепла окажется выше, чем скорость его выделения. Раз так, то после снятия возмущения реактор начнет охлаждаться. Охлаждение будет продолжаться до тех пор, пока реактор не вернется к температуре Т1. При этой температуре скорости выделения и отвода тепла опять уравняются и режим снова станет стационарным. Наоборот, если в результате возмущения реактор слегка охладится, то скорость выделения тепла станет больше, чем скорость его отвода и реактор начнет нагреваться, пока снова не достигнет Т1. Таким образом, при температуре Т1 режим устойчив. При температуре Т3 с точки зрения устойчивости картина полностью аналогична предыдущему режиму. Прямая теплоотвода также идет круче, чем кривая выделения тепла. Точно такие же рассуждения приводят к такому же выводу: режим устойчив. Теперь обратимся к точке 2. Здесь наклон прямой теплоотвода меньше, чем наклон кривой выделения тепла. Так же, как и в точках 1 и 3, Q1 = Q2, и если нет возмущений, режим будет оставаться стационарным. Но предположим, что произошло случайное возмущение – повышение температуры до T2 + dT. При этой температуре скорость выделения тепла станет большей, чем скорость теплоотвода. После снятия возмущения реактор будет не охлаждаться, а нагреваться, удаляясь от начального состояния. Нагревание будет продолжаться до тех пор, пока при температуре T3 реактор не придет в устойчивое стационарное состояние. Точно так же при случайном охлаждении реактор будет самопроизвольно охлаждаться до тех пор, пока не дойдет до устойчивого состояния при Т1. Итак, из трех возможных в данных условиях стационарных режимов два – при низкой температуре (и малой скорости реакции) и при высокой температуре (и большой скорости реакции) – устойчивы, а третье – при промежуточных температуре и скорости реакции – неустойчиво. Условие dQ2/dT>dQ1/dT. Отличие около состояния 2 как неустойчивого. Автоматика или интенсификация отвода тепла у точки 2 как модератор системы. Иначе CT/t+KTFT/Va>Qpdr/dT, где FT/Va=fT – удельная поверхность, падает с ростом объема. Условие устойчивости в этой задаче состоит в том, что прямая теплоотвода идет круче, чем прямая тепловыделения. Это условие можно записать формулой Что делать, если желательно работать в области температур вблизи T2? Есть два выхода: один – построить систему автоматического регулирования, которая будет удерживать режим в неустойчивом состоянии, второй – сделать теплоотвод столь интенсивным, что линия отвода тепла будет всюду круче линии выделения, как это показано на рис. 6.7. Рис. 6.7. Зависимости Q1 и Q2 от Т при устойчивости во всем диапазоне Т Подставив в формулу (6.12) выражения для Q1 и Q2 из (6.9), после несложных преобразований получим условие устойчивости в виде Коллизия размера и устойчивости. Заметим, что левая часть будет большой при условии интенсивного теплообмена, т.е. когда велики Кт и удельная поверхность fт = Fт / Va. Это указывает путь к повышению устойчивости. Но одновременно учтем следующее. Если размер аппарата уменьшается, то величина fт растет. Поэтому условия работы малой модели могут соответствовать зависимости, показанной на рис. 6.7, при этом неустойчивость не возникает. При переходе к большим размерам установки fт уменьшается и возможно неожиданное возникновение неустойчивости. В серьезных технологических разработках необходимо анализировать параметрическую чувствительность и устойчивость методами математического моделирования. Подобие с зерном непористого катализатора. Рост температуры в ядре потока – перенос прямой вправо до касания (неустойчивость). Зажигание катализатора. Падение температуры – перенос влево до касания (неустойчивость). Погасание катализатора при более низкой т-ре, чем зажигание. Зажигание катализатора. Зависимость скорости реакции на непористом катализаторе от температуры поверхности, близка к зависимости, показанной на рис. 6.5. В случае экзотермической реакции выделяющееся тепло отводится в поток газа или жидкости. Уравнение (5.70), так же как и баланс (6.9), сводится к записи Q1 = Q2. При этом изменение температуры в ядре потока Тя вызывает на графике параллельный перенос прямой теплоотвода: чем выше Тя, тем правее пройдет эта прямая (рис. 6.8). Рассмотрим с помощью этого рисунка процесс постепенного повышения Тя. Пока эта температура растет от Т1 до Т5, процесс на зерне устойчиво удерживается в кинетической области (пересечение прямых с нижней частью кривой выделения тепла). При достижении в ядре потока температуры Т5 произойдут скачкообразный рост температуры Тп и переход в диффузионную область – зажигание катализатора. Зажигание связано с потерей устойчивости низкотемпературного процесса: в точке, где прямая 5 касается кривой, процесс уже неустойчив. После зажигания устойчивым становится процесс, соответствующий верхней части кривой Q1. Он будет устойчив даже, если температура Тя начнет понижаться. Лишь при достижении в ядре температуры Т2 (прямая 2) устойчивость будет потеряна, температура скачком упадет, процесс перейдет в кинетическую область – произойдет погасание катализатора. Гистерезис! Прямая 2 на рис. 7.2. Кинетическая и диффузионная область. Неустойчивость в изотермических режимах. Проанализируем простой случай: процесс стационарен, проходит изотермически. Не углубляясь в механизм каталитической кинетики, будем считать, что реакция необратима, имеет 1-й порядок, а ее скорость где cп – концентрация реагирующего вещества A непосредственно у поверхности. Для реакций не 1-го порядка закономерности качественно близки к тем, которые получаются в анализируемом случае. Рассмотрим материальный баланс по реагенту А. В уравнении баланса присутствуют только два члена: вход и сток (уход и источник равны нулю – реагент не поступает с поверхности в поток и не образуется, так как реакция необратима; накопление тоже равно нулю ввиду стационарности). Окружим контуром малый участок каталитической поверхности, площадь которого примем за единицу; за интервал примем единицу времени (интервал конечен, так как процесс стационарен). Тогда вход А будет равен потоку вещества на поверхность, а сток – скорости гетерогенной реакции. Уравнение при этом принимает вид Уравнение (5.44) выражает свойство аддитивности сопротивлений. Коэффициенты β, k и k′– скоростные коэффициенты: скорости процессов им пропорциональны. Обратные величины называют сопротивлениями. Формулу (5.44) можно прочесть так: общее сопротивление процессу 1/ k′ складывается из сопротивлений стадий: диффузионного 1/β и кинетического 1/k. Аддитивность сопротивлений говорит о том, что процесс складывается из последовательных стадий и что лимитировать будет медленная стадия. Рассмотрим, от чего и как будет зависеть скорость процесса при наличии лимитирования. Здесь только необходимо учесть вот что. Из уравнения (5.39) следует, что скорость потока вещества А к поверхности равна скорости реакции. В этом смысле в стационарном случае нельзя говорить о медленной и быстрой стадиях – их скорости равны. Но сравнивать можно и по-другому: считая мерой скорости среднее время, затрачиваемое молекулой в одной стадии на преодоление пограничного слоя, а в другой – на химическое превращение после того, как она достигла поверхности. Тогда скорости становятся разными и их можно сравнивать. Случай 1 : k << β, медленная реакция при быстром транспорте вещества к поверхности. Каковы основные закономерности этого случая? Из вышесказанного ясно, что лимитирующая стадия – протекание химической реакции на поверхности. Реакция проходит в кинетической области. Для уточнения особенностей этой области обратимся к уравнениям (5.38) – (5.44). Из (5.40) следует, что сп ≈ ся: быстрая диффузия выравнивает сА по толщине пограничного слоя, медленная реакция «не в силах» существенно снизить эту концентрацию. Из (5.44) получим, что k′≈ k, так как малым слагаемым 1/β можно пренебречь по сравнению с большим 1/k. Теперь из (5.42) находим: В уравнении (5.45) ничто не связано с процессом диффузии, все определяется через закономерности кинетики. Случай 2 : k >> β, быстрая реакция при медленной диффузии. Лимитирует подвод реагента через пограничный слой. Процесс идет в диффузионной области (внешнедиффузионной, диффузия проходит вне гранулы катализатора). Снова обратимся к уравнениям (5.38) – (5.44). Из (5.40) следует, что сп ≈ 0: знаменатель дроби много больше, чем числитель. Из (5.44) получим, что k′≈ β. Тогда уравнение (5.42) можно записать в виде Правую часть выражения (5.46) я записал так, чтобы было ясно: это уравнение массоотдачи для случая, когда концентрация со стороны твердой поверхности практически равна нулю. Случай 3 : коэффициенты k и β сравнимы по величине. Ни одна из стадий не лимитирует процесса – он проходит в промежуточной (переходной) области. Скорость реакции рассчитывается по формуле (5.41). Какие условия способствуют увеличению скорости массоотдачи? В первую очередь это рост скорости потока. В то же время скорость потока непосредственно не влияет на химическую кинетику. Поэтому если процесс проходит в кинетической области, поток не влияет на его скорость; если в диффузионной, то увеличение скорости потока ускоряет процесс, а если в промежуточной, то при увеличении скорости потока процесс может перейти в кинетическую область. Какие условия способствуют ускорению собственно реакции? Как уже говорилось, сильнее всего константа скорости реакции зависит от температуры. В то же время скорость массоотдачи слабо зависит от температуры, в особенности если движущая фаза – газ. В связи с этим кривая зависимости скорости реакции от температуры имеет характерный вид (рис. 5.9). В области низких температур общая скорость процесса сравнительно мала, но при этом с повышением температуры она резко возрастает в соответствии с уравнением Аррениуса. Процесс идет в кинетической области. При повышении температуры рост скорости процесса замедляется и начиная с некоторой температуры почти прекращается. Процесс вступает в диффузионную область. Если увеличить скорость потока, т. е. снизить диффузионное торможение (верхняя кривая на рис. 5.9), то в кинетической области кривая пойдет точно так же, но промежуточная и диффузионная области начнутся при несколько более высоких температурах, а общая скорость процесса в этих областях окажется выше. Рис. 5.9. Зависимость скорости реакции от температуры для непористого катализатора. Области: 1 – кинетическая; 2 – промежуточная; 3 – диффузионная Общие проблемы науки (нелинейность, обратные связи). Внешние связи системы. Определяя понятие «система», я уже говорил об исключительной важности связей между ее элементами. Для динамических систем не менее важны внешние связи – взаимодействия системы с окружающим ее миром. Внешние связи бывают двух основных классов: воздействия мира на систему – входы системы и воздействия системы на мир – ее выходы, результат функционирования системы. Особый случай – обратные связи: выход системы оказывает влияние на ее вход. Существуют положительные обратные связи, когда усиление выходного сигнала усиливает сигнал на входе, и отрицательные обратные связи, когда с усилением выходного сигнала входной ослабляется. Как правило, действие положительных обратных связей приводит к возбуждению системы, интенсификации ее деятельности; в неблагоприятных случаях это может привести к тому, что система «пойдет вразнос». Наоборот, отрицательные обратные связи стабилизируют состояние системы. Фазовые координаты, аттракторы (узлы), репеллеры, седла, предельные циклы (перерегулирование, колебательные химические реакции). Странный аттрактор, хаос, турбулентность. Численное моделирование – проблема хаоса. Некоторые особенности задач, связанных с устойчивостью. При описании задач, связанных с устойчивостью, часто бывает удобно изображать состояние системы в фазовых координатах. По осям координат откладываются значения параметров, определяющих состояние системы. Точка в фазовом пространстве соответствует какому-либо из таких состояний. При этом если мы рассматриваем изменение фазового графика во времени и если точка неподвижна, значит, состояние системы стационарно; нестационарный режим изображается движущейся точкой. Что отличает в фазовом пространстве неподвижные точки, соответствующие устойчивым или неустойчивым стационарным состояниям? Если состояние, изображаемое точкой, устойчиво, то около нее имеется область, в которой все возможные траектории нестационарных процессов движутся в направлении этой точки. Переходные процессы заканчиваются стационарным состоянием. Такие точки называют аттракторами. Напротив, точку, изображающую неустойчивое стационарное состояние, окружает область, где все траектории направлены прочь от этой точки. Такую точку называют репеллером (от лат. attraho – притягивать, repello – отталкивать). Бывает и так, что малое число траекторий (обычно – две) направлены к данной точке, а остальные – от нее. Это случай седловой точки. Что может произойти, если система вышла из неустойчивого состояния и предоставлена самой себе? Простейший вариант, к которому сводились рассмотренные выше случаи: вблизи данного репеллера отыщется аттрактор и точка перейдет в него, система окажется в ином, уже устойчивом состоянии. Но возможны и другие варианты. Один из них таков. Точка начинает двигаться по замкнутой кривой, совершая один оборот за другим. Такую кривую называют предельным циклом. Движение точки по предельному циклу отображает протекание на объекте колебательного процесса, параметры которого периодически изменяются во времени. Так ведут себя многие процессы при перерегулировании: вместо того чтобы под воздействием регулятора прийти к заданному режиму, процесс начинает совершать непрерывные колебания [13]. То же наблюдается при возникновении колебательных химических реакций [39]. В последние десятилетия обнаруживается еще один возможный вариант, обозначаемый термином «странный аттрактор». Странный аттрактор – это не точка, а целая область в фазовом пространстве, обладающая двумя свойствами. Во-первых, это аттрактор – точка, попавшая в его окрестность, будет двигаться к нему и затем войдет внутрь. Во-вторых, внутри странного аттрактора существует множество (теоретически бесконечное) возможных траекторий, но все они неустойчивы. Точка, вошедшая в странный аттрактор, начнет двигаться по какой-либо траектории, но вследствие неустойчивости этого движения при малейшем возмущении перескочит на другую «случайно подвернувшуюся» траекторию, затем на третью и т.д. Система войдет в режим хаотических колебаний. Пример 6.2. Ламинарное течение жидкости при постоянном расходе стационарно. Но если скорость превысит предел, определяемый критическим значением критерия Re, то ламинарное течение становится неустойчивым и поток эволюционирует в сторону странного аттрактора – турбулентного режима, в котором траектория движения любой частицы неустойчива и поэтому претерпевает хаотические пульсации. Автокатализ и устойчивость. Затравка в биотехнологии. Проблемы экологии и устойчивость. Устойчивость режимов при автокатализе. Рассмотрим еще одну задачу, представляющую заметный интерес для химиков. В аппарате идеального смешения при постоянных температуре и расходе жидкости проводится реакция Таким образом, вещество В является и продуктом реакции, и катализатором. Такая схема реакции – простейшая модель процессов типа ферментации, протекающих под воздействием микроорганизмов (об этом я уже упоминал в разд. 4.2). В этом случае вещество А – субстрат, т.е. пища для бактерий или грибков; С – тот продукт, который следует получить; В – сами микроорганизмы. Они выступают в роли и катализатора, потому что без них реакция не идет, и продукта: поедая субстрат, они размножаются, и чем больше потреблено пищи, тем больше их образовалось. Существенная особенность процесса: сВ0 = 0. Это обусловлено тем, что входящий поток субстрата стерилизуют, поскольку иначе на вход могут попасть так называемые «дикие расы» микроорганизмов, бесплодные, но хорошо приспособленные к конкуренции и культурная раса В окажется вытесненной. Анализ, скорее всего, не нужен. реакция не начнется, сколько бы ни продолжать продукты образовываться не будут. Второе решение относится к случаю, когда вначале в аппарате присутствовало вещество В (была введена затравка микроорганизмов), реакция началась и хотя в установившемся стационарном режиме катализатор не вводится он образуется в результате реакции и поддерживает ее протекание. Возникает вопрос об устойчивости: что произойдет, если концентрация вещества В случайно слегка изменится? Выправится в дальнейшем это изменение или окажется, что из аппарата выносится больше катализатора, чем образуется, и в конце переходного периода вещества В не останется, реакция прекратится и реализуется первое решение? Рис. 6.9. Изменение концентрации вещества А в переходном процессе Снова обратимся к уравнению (6.19). Правая его часть – это квадратный трехчлен относительно сА, причем член, содержащий квадрат, положителен. График зависимости представляет собой параболу с минимумом, находящимся между корнями трехчлена (рис. 6.9). А это значит, что если значение концентрации сА окажется между обоими стационарными значениями, производная по времени будет отрицательной, концентрация реагента станет уменьшаться, приближаясь к значению . Таким образом, первое из этих значений относится к устойчивому режиму, второе – к неустойчивому. Во-первых, кривая на рис. 6.9 справа не заходит дальше значения сА = сА0, поскольку правее от этой точки условие (6.15) означало бы отрицательную концентрацию вещества В, что невозможно. Рис. 6.10. Траектории переходных процессов в фазовых координатах для автокаталитической реакции Устойчивость экосистем. Очень часто по тому же механизму потери устойчивости происходит разрушение биоценозов. Биоценоз – это система, состоящая из всех живых организмов (животных, растений, бактерий и др.), населяющих какой-либо участок Земли. При выбросе в окружающую среду вредных веществ в биоценозе развиваются компенсаторные механизмы, нейтрализующие вредные влияния. Поэтому до определенного предела среда ведет себя «почти нормально» – нормальное состояние устойчиво. Но при повышении загрязнения до некоторого критического уровня устойчивость теряется и биоценоз сразу, скачком, гибнет. Непонимание этого порождает неоправданное благодушие: дескать, выбрасываем отбросы – природа справляется; выбросим еще немного – тоже справится, в худшем случае станет немного грязнее. На деле требуются чрезвычайная осторожность и тщательное изучение устойчивости окружающей среды, а также огромная работа по повышению этой устойчивости. 5. Оптимизация Теоретические вопросы. Общий подход к задачам: формализация (приоритет общего по отношению к частному), алгоритм (стандартность), реализация алгоритма. Вариантность. Первый этап – решающий. Для современного подхода к оптимизации характерна формализация задачи. Задача формулируется стандартным образом, после чего дальнейшее ее решение проводится на основе четкого однозначного рецепта – алгоритма. Однозначность в данном случае не означает, что отсутствуют варианты решений. Наоборот, проводится сравнение многих различных вариантов. Но алгоритм точно определяет, на каком этапе и как производится такое сравнение. Формализация, во-первых, позволяет единообразно решать задачи из самых различных областей. Во-вторых, формализованные задачи приспособлены для решения на компьютерах. Применение вычислительной техники обеспечивает возможность перебора очень большого числа вариантов и выбора из них наилучшего. Поэтому формализация резко повышает эффективность процедуры решения задачи. При формализации задачи оптимизации возникает важное противоречие. Задача распадается на три основных этапа: 1) формулирование задачи, приведение ее к одной из стандартных форм; 2) нахождение оптимальных условий на основе алгоритма оптимизации; 3) реализация оптимальных условий на практике. Методы решения на первом и втором этапах взаимно противоположны: второй этап, как правило, целиком формализован на основе алгоритма решения, а первый этап – неформален. Здесь не поможет никакая математика. Первый этап решения задачи связывает конкретные особенности объекта с общим методом решения. Если задача оптимизации плохо сформулирована, то совершенно правильное ее решение даст результат, абсурдный для практики. Иногда именно хорошая формулировка задачи определяет успех оптимизации в целом. Некоторые проблемы, возникающие при формулировании задач оптимизации, проиллюстрируем на примерах. Таким образом, на этапе формулирования задачи приходится учитывать физикохимические особенности процесса, его экономичность, общее развитие промышленности, рыночную конъюнктуру и множество других обстоятельств. Как правило, формулировка задачи оптимизации включает выбор критерия оптимальности, установление ограничений, выбор оптимизирующих факторов и запись целевой функции. Критерий, множество критериев, выбор главного, корректность выбора. Универсальный подход ко многим задачам, которые можно решать иначе. Родство к подбору критерия. Формулировка задачи. Выбор критерия оптимальности. Требования: единственность (экономика, технология, экология…); численность (баллы для качественных задач); монотонная зависимость от факторов как основное средство против множественности решений. Критерий оптимальности – это главный признак, по которому судят о том, насколько хорошо функционирует система, работает данный процесс, насколько хорошо решена задача оптимизации. О работе судят по ее результатам. Поэтому критерий оптимальности является одним из результатов работы, одним из выходов системы. Чтобы выбранный критерий оптимальности можно было эффективно использовать на следующем этапе, он должен удовлетворять трем основным требованиям. 1. Критерий оптимальности должен быть единственным. Это самое тяжелое требование. Дело в том, что, как правило, нас интересует ряд выходов системы и мы хотим, чтобы по всем им система была наилучшей. Иногда говорят так: оптимальным является такое ведение технологического процесса, при котором производительность установки и качество продукта максимальны, а затраты и потери минимальны. При внешней привлекательности такая постановка задачи утопична и потому объективно вредна. Так вести процесс невозможно. Обычно наиболее обоснованы такие экономические критерии, как прибыль, норма прибыли, рентабельность, приведённый доход, себестоимость. Однако чаще всего характер зависимости этих критериев от входных параметров системы сложен. Для упрощения задачи зачастую пользуются технологическими критериями, например производительностью, чистотой продукта, выходом продукта, селективностью. Каждый технологический критерий в конечном счете связан с экономикой: чем больше производительность, тем выше будет прибыль; чем выше чистота, тем меньше будут затраты на следующих стадиях, и т. д. При оптимизации производства в целом или его крупных подразделений естественно использовать экономические критерии. Технологические критерии удобны при оптимизации более мелких объектов: отдельного узла, аппарата, небольшой цепочки аппаратов, т. е. при локальной оптимизации. При их применении следует особенно тщательно учитывать особенности процесса: критерий, пригодный в одних условиях, может быть совершенно не применим в других условиях. 2. Критерий оптимальности должен выражаться числом. В противном случае сопоставление разных вариантов становится крайне затруднительным. 3. Обязательное и крайне важное свойство критерия оптимальности: его величина должна изменяться монотонно при улучшении качества функционирования системы. Это значит, что оценивать объект можно по принципу: «чем больше критерий, тем лучше», либо «чем меньше критерий, тем лучше», но ни в коем случае не по принципу: «вот это значение критерия оптимально и отклоняться от него не следует». Что требуется, «больше» или «меньше», определяется физическим или экономическим смыслом критерия. Хорошо, когда прибыль велика, но когда себестоимость мала; когда велика производительность, но малы потери. Умножив любой критерий на –1, мы превратим «больше» в «меньше» и наоборот. Но вот критерий, обладающий некоторым оптимальным значением, от которого нежелательно отклоняться, не годится. Например, в лекарственной смеси содержание того или иного ингредиента не может являться критерием оптимальности: иначе мы бы получили не смесь заданного состава, а максимальную концентрацию одного вещества. Если для какого-то параметра, характеризующего систему, существует оптимальное значение, то либо этот параметр – не критерий оптимальности, а оптимизирующий фактор (см. ниже), либо критерием является не величина параметра, а отклонение этой величины от заданного значения. Ограничения – категорические условия (дополнительные критерии, предельные возможности по количеству, качеству, технологии, экономике, конъюнктуре, охране труда и среды обитания…). По форме это равенства и неравенства. Ограничения - Условия, которые необходимо соблюдать независимо от того, как их соблюдение повлияет на величину критерия оптимальности. Следующие группы ограничений: • по количеству и качеству сырья и продукции – состав сырья, как правило, задается не нами и менять его нельзя; количество сырья также может быть ограничено; выпуск продукции не должен быть больше того, что можно реализовать; качество продукта не должно быть ниже стандарта или требований заказчика; • по условиям технологии – расход воздуха не может превышать производительность вентилятора; температура не может быть выше предела, при котором портится материал аппарата или катализатор; размеры аппаратов изменять мы не можем и т. д.; • по экономическим и конъюнктурным соображениям – капитальные затраты не должны превышать выделенной суммы; срок ввода нового производства не должен быть позже запланированного; нельзя применять методы и устройства, защищенные чужими патентами; • по соображениям охраны труда и окружающей среды – это чрезвычайно важная группа ограничений, жесткость которых все возрастает. Кроме классификации по смыслу ограничения можно различать по формальноматематическим признакам. Так, выделяют ограничения типа равенств и типа неравенств. Ограничения типа равенств устанавливают определенное значение того или иного параметра: Здесь fi – один из параметров, аi – задаваемое для него значение. Например, в конкретных условиях работы задаются численные значения, характеризующие состав сырья, размеры аппаратов, нагрузку на аппарат и т. д. Ограничения типа неравенств определяют пределы, в которых допустимо изменение параметров процесса: Два первых ограничения (7.3) задают односторонние пределы (например, производительность не ниже заданной; температура не выше той, на которую рассчитан материал). Третье ограничение – двустороннее (например, температура жидкости в пределах от температуры замерзания до температуры кипения). Ограничения 1-го рода: на входные факторы; 2-го рода: на промежуточные и выходные величины, что сложнее. Наконец, в расчетных процедурах нахождения оптимума большую роль играет деление ограничений по следующему признаку: ограничения 1-го рода – условия (7.2) или (7.3), где в качестве параметров f фигурируют входные факторы; ограничения 2-го рода, где параметрами служат различные функции входов, например результаты процесса или, скажем, температуры в каких-то точках внутри аппарата. Оптимизирующие факторы – управляемые входы (температура…). Оптимизирующие факторы – те из входов системы, которые в процессе оптимизации относят к управляющим. Это те воздействия, которые мы применяем для оптимизации процесса. Остальные факторы при этом не регулируются, хотя их значения, разумеется, учитывают при определении оптимальных условий: эти факторы фигурируют в задаче в качестве ограничений типа равенств. Оптимальное проектирование – много факторов (недорого на модели). Оптимальное управление (динамическое программирование) – факторов поменьше. Число оптимизирующих факторов зависит от того, на какой стадии разработки производства осуществляется оптимизация. Если производство еще проектируется (оптимальное проектирование), то к оптимизирующим целесообразно отнести как можно большее число факторов. Действительно, на этой стадии варьировать факторы проще всего: изменение значений осуществляется не в действительности, а на математической модели. Поэтому здесь желательно найти оптимальные значения максимального числа факторов. Но задача оптимизации возникает и после пуска производства (оптимальное управление). При этом число оптимизирующих воздействий становится существенно меньшим. Часть факторов мы уже не можем менять, например размеры аппаратов. Но и не все остальные факторы целесообразно теперь регулировать. Дело в том, что чем больше управляющих факторов, тем сложнее система управления, сложнее ее математическая модель. При очень большом числе факторов она может стать столь сложной, что компьютер, рассчитывающий оптимальные режимы, перестанет поспевать за изменением условий протекания процесса: рекомендации по оптимизации придут, когда реализовать их уже поздно. Все это заставляет использовать для оптимального управления сравнительно небольшое число факторов. Целевая функция – критерий оптимальности, его экстремум, оптимальные значения факторов при нем. Функционал, распределенные факторы, характер распределения. Условный экстремум (на границе, при ограничениях и т.п.). Целевая функция – это синоним критерия оптимальности, но это критерий, рассматриваемый как функция входных факторов: Чем больше (или чем меньше) значение F, тем лучше. Поэтому можно дать такое определение оптимума: оптимум – это экстремум (либо максимум, либо минимум) целевой функции. Те значения факторов хj, при которых достигается оптимум, называют оптимальными. Таким образом, математически задача оптимизации формулируется как задача отыскания экстремума. При этом в точке экстремума должны соблюдаться все ограничения. Поэтому во многих случаях оптимум приходится искать на краю области допустимых значений, за пределы которой нельзя выйти из-за ограничений (рис. 7.1). На рисунке отрезок аb есть область допустимых значений, определяемая ограничением a ≤ x ≤ b. Максимум функции F расположен правее точки b, но оптимальным будет значение x = b, поскольку большие значения х запрещены ограничением. Рис. 7.1. Целевая функция с оптимумом на краю допустимой области Методы отыскания оптимума: - аналитические (на основе вариационного исчисления), они играют роль теоретической основы - численные (поисковые, при вычислимой функции, в т.ч. при неявной форме уравнений относительно выходных величин) - экспериментальные (при невычислимой, но воспроизводимой функции). Методы отыскания оптимума можно разделить на три основные группы. 1. Аналитические методы. Их применяют, например, когда мы можем продифференцировать целевую функцию и искать экстремум исходя из условия равенства нулю производных. Условие отыскания экстремума при аналитической оптимизации нулевое значение 1-х производных по факторам одинаковом знаке 2-х. 2. Численные, или поисковые методы. Для их применения нужно, чтобы целевая функция была вычислимой : должен быть известен алгоритм, по которому можно рассчитать значение критерия оптимальности при заданных значениях факторов. 3. Методы, применяемые, если целевая функция невычислима. Практически это значит, что вид функции неизвестен. Тогда остается одно: планировать и реализовывать эксперимент так, чтобы в результате достигнуть района оптимума. Это – экспериментальная оптимизация, составляющая важный раздел планирования эксперимента. Максимум и минимум. Седла и перегибы, локальность, ограничения, нормальные уравнения. Множественность решения: глобальность и локальность. Поверхность отклика, ее симметрия как источник глобальной и локальной неоднозначности. Пусть целевая функция задана формулой (7.4). Классический метод отыскания экстремума заключается в решении системы Левые части уравнений (7.5) – функции от факторов х1, х2, ..., хn. Поэтому решение системы может дать значения x1опт , x2опт , ..., xnопт , являющиеся оптимальными значениями факторов; их совокупность определяет наилучшее решение задачи. Если оптимизируется технологический процесс, то этому решению соответствует оптимальный режим. Однако следует убедиться, что полученные значения действительно оптимальны. Для этого необходимо выяснить: 1) действительно ли решение системы (7.5) определяет экстремум, поскольку известно, что условию (7.5) может удовлетворять и седловая точка, или точка перегиба; 2) получен ли экстремум нужного знака (максимум, если нас интересует максимум, или минимум в обратном случае); 3) если система имеет несколько решений, то какое из них отвечает глобальному оптимуму, а какие – локальным. Так, если зависимость имеет несколько максимумов, то глобальным будет тот из них, который выше всех остальных; остальные будут локальными; 4) все ли ограничения соблюдаются в точке экстремума. Рассмотрим некоторые важные задачи оптимизации. Одна из разобранных выше задач, а именно расчет коэффициентов методом наименьших квадратов (см. разд. 2.3) – типичная задача такого рода. В ней критерий оптимальности – сумма квадратов S; оптимизирующие факторы – значения рассчитываемых параметров. Ограничения в изложенном варианте отсутствуют. Система (7.5) – это система нормальных уравнений (2.42). Примеры решаемых небольших задач. Сложные или объемистые задачи – для численных методов. Обратимая экзотермическая реакция первого порядка, оптимальная температура: Топт=(Е2-Е1)/(Rln(A2/A1E2/E1CB/CA)). Если химическая реакция проходит без побочных стадий, то удается принять очень простой критерий оптимальности – скорость реакции (см. пример 7.2). Согласно схеме, данной в предыдущем разделе, теперь нужно установить ограничения и выбрать оптимизирующие факторы. Но часто бывает удобно сначала записать целевую функцию, а уже потом перейти к ограничениям и оптимизирующим факторам. Так поступим и мы. Для определенности рассмотрим реакцию Таким образом, наш критерий зависит от трех параметров: температуры и концентраций сА и сВ. По-видимому, эти три величины можно было бы избрать в качестве оптимизирующих факторов. Но необходимо учесть, что концентрации сА и сВ не относятся ко входам рассматриваемой системы. Они сами получаются как результат реакции. Ясно, что для увеличения скорости следовало бы иметь как можно большее значение сА и как можно меньшее значение сВ. Цель же процесса – противоположная: увеличить сВ и уменьшить сА. Поэтому концентрации нельзя рассматривать как независимые факторы. Итак, есть лишь один независимый фактор, которым можно влиять на F – температура. Рассматриваемая задача обычно называется задачей об оптимальной температуре химической реакции. Но при разных концентрациях влияние температуры может быть различным. Поэтому будем решать задачу в такой постановке: зафиксируем некоторые значения сА и сВ и при этих значениях найдем оптимальную температуру. Таким образом, в данном решении концентрации веществ А и В выступают в роли ограничений типа равенства. Кроме того, учтем одно ограничение типа неравенства, которое существует в любой практической задаче: температура не может превысить некоторого максимального значения Тмакс : Прежде чем обращаться к формуле (7.5), рассмотрим два случая, когда оптимум можно найти из физических соображений, без расчета. Если реакция необратима, т. е. А2 = 0, то в правой части формулы (7.6) остается только первый член, который с повышением температуры все время растет. Максимум в смысле условия (7.5) отсутствует. Тогда оптимум определяется ограничением: следует поддерживать максимально допустимую температуру Если реакция обратима, но эндотермична, т. е. E1 > E2, то результат рассуждений тот же, что и в предыдущем случае. Действительно, с повышением температуры равновесие сдвигается вправо и скорость прямой реакции возрастает. Поэтому оптимум определяется формулой (7.6). Если реакция – обратимая экзотермическая, то к решению потребуется применить иной подход. В этом случае с повышением температуры вначале более существенным будет возрастание скорости прямой реакции; обратная еще слишком медленна. При дальнейшем увеличении температуры обратная реакция, имеющая большую энергию активации, начинает «нагонять» прямую. При данном составе смеси существует температура Tравн, при которой смесь находится в равновесии: r = 0; затем ход реакции смещается влево. Где-то посередине имеется температура, при которой суммарная скорость реакции максимальна. Это и есть оптимальная температура Топт . Для ее расчета запишем условие (7.5) для формулы (7.6): Здесь записана частная производная по T, поскольку она берется при фиксированных значениях cA и cB. Из уравнения (7.9) несложными преобразованиями можно получить формулу для оптимальной температуры: Ступенчатое охлаждение. Из соотношения (7.10) следует, что чем выше cA и чем меньше cB, тем выше Топт; по мере роста степени превращения величина Топт уменьшается. При cB→0, согласно формуле, Топт →∞. Поэтому на начальном участке реактора следует устанавливать максимально допустимую температуру Tмакс, а с момента, когда рассчитанная по этому уравнению Топт сравнивается с Tмакс, дальнейшее изменение температуры должно определяться уравнением (7.10). Такую зависимость иллюстрирует кривая 1 на рис. 7.2, изображающая оптимальный ход температуры в зависимости от степени превращения. Рис. 7.2. Изменение оптимальной температуры в зависимости от степени превращения для обратимой экзотермической реакции Реально осуществить такое распределение температуры чрезвычайно трудно. Действительно, на начальном участке следовало бы поддерживать постоянную максимальную температуру, что крайне сложно: здесь скорость реакции очень велика, выделение тепла максимально и полностью отвести его вряд ли удастся. Поэтому применяют другие распределения, более или менее приближающиеся к оптимальному. Так, ломаная 2 на рис. 7.2 показывает ход температуры в пятислойном каталитическом реакторе, в каждом слое которого реагирующая смесь адиабатически разогревается за счет тепла реакции, а между слоями охлаждается в теплообменнике. Такое распределение температур приведет к несколько худшим результатам (большему потребному объему катализатора), чем задаваемое кривой 1, но его сравнительно легко осуществить. Чем больше ступеней катализа, тем ближе ломаная к оптимальной кривой. Если реакцию проводят в аппарате смешения, то во всем его объеме имеем одну и ту же степень превращения. Ей соответствует одна точка на кривой 1 (см. рис. 7.2), соответствующая оптимальной температуре для данного аппарата. Параллельно работающие аппараты ИС. Первый порядок, необратимо, проскок – это потеря. Оптимальное распределение потока по параллельно работающим аппаратам. Это одна из задач, возникающих при оптимальном управлении. Рис. 7.3. Схема распределения потока по аппаратам Реакция 1-го порядка А → В проводится в n параллельно соединенных реакторах идеального смешения (рис. 7.3). Как оптимально распределить поток между аппаратами? Будем считать, что в общем случае объемы аппаратов V1, V2, …, Vn разные и что константы скорости реакции в различных аппаратах k1, k2, …, kn тоже разные (например, вследствие неодинаковой активности катализатора). Естественно принять за критерий оптимальности сумму потерь вещества А, т. е. считать наилучшим такое распределение, при котором потери вещества А вследствие неполноты реакции минимальны. В каждом i-м аппарате при расходе vi эти потери в единицу времени составляют vi*cAi; тогда для всех аппаратов можно записать: Обозначим kiVi = ai. Величина ai характеризует относительную производительность i-го аппарата: чем больше эта величина, тем больше продукта может получиться в нем в единицу времени. Теперь можно записать: Прежде чем применить к целевой функции (7.12) условие (7.5), обратим внимание на существующее в этой задаче ограничение типа равенства: сумма расходов через все аппараты равна общему расходу через систему: Учтем, что частная производная от этого выражения по любому vi равна –1, поскольку v – постоянная, а под знаком суммы от vi зависит только один член, а именно vi , и частные производные от всех остальных членов равны 0. Тогда по теореме о производной функции от функции для производной по любому vi любой функции f от vn будем иметь: При оптимальном распределении расход через каждый аппарат пропорционален относительной производительности этого аппарата. Чем больше аi , тем больше vi . Простое преобразование формулы (7.18) дает При оптимальном распределении потока концентрации вещества на выходе из всех аппаратов одинаковы. Условие (7.19) позволяет просто осуществлять оптимальное регулирование распределения потока: концентрация вещества А на выходе из всех аппаратов должны быть одинаковой; если в каком-то аппарате она больше, чем в остальных, расход из этого аппарата следует уменьшить, и наоборот, если сА меньше средней, расход надо увеличить. Оптимальный режим достигается при равных выходных концентрациях: простое управление при разных константах скорости (катализ, температура, объем). Численные методы. Аналитическую производную трудно, а чаще невозможно вывести: дискретность, край области, алгоритмическое задание критерия, громоздкость. Поэтому превалируют численные методы. Простой перебор (варианты, включая Монте-Карло). Сканирование (непрерывные функции, но не только). Узлы. Одномерное сканирование. Управление шагом. Выбор интервала неопределенности. Правило останова Поиск оптимума численными методами Численные методы поиска применяют, во-первых, когда в точке экстремума отсутствуют производные. Так, изменение целевой функции может носить дискретный характер, например при сравнении разных вариантов оформления процесса, когда F меняется не непрерывно, а скачком от одного варианта к другому. Но производные в точке экстремума могут отсутствовать и у непрерывной функции. Как правило, это происходит, если экстремум расположен на краю области допустимых значений. На рис. 7.1 максимум лежит на краю области, в этой точке производная отсутствует. Имеется «производная слева», но она не равна нулю. В задачах оптимизации такую точку рассматривают как «законный» экстремум (в данном случае – максимум). Часто бывает и так, что целевая функция в точке экстремума дифференцируема, но она задана таким образом, что продифференцировать ее в общем виде не удается, вследствие чего приходится обращаться к численным методам. Это обычно связано с тем, что функция задана не формулой, а алгоритмом вычисления при заданных значениях аргументов (факторов). Если бы не было и алгоритма, функция была бы невычислимой и следовало бы применить экспериментальную оптимизацию (см. разд. 7.4). Наконец, иногда имеется принципиальная возможность записать и решить систему (7.5), но соответствующие вычисления столь громоздки, что численный метод оказывается проще. В наиболее общем виде численные методы сводятся к тому, что вычисляется ряд значений F при различных значениях аргументов; сопоставление этих значений показывает, в каком направлении нужно двигаться в пространстве факторов, чтобы приблизиться к оптимуму. Оптимизация перебором применяется, если число возможных вариантов конечно. Тогда достаточно рассчитать целевую функцию для всех этих вариантов и выбрать наибольшее (или наименьшее) значение. Например, мы можем рассчитать F для случаев протекания процесса в аппаратах всех стандартизованных размеров и выбрать лучший вариант. Перебор легко осуществляется на компьютере, причем все варианты (например, нормали) могут быть заранее записаны в памяти машины. Несмотря на крайнюю простоту метода, он часто оказывается чрезвычайно эффективным, поскольку возможности перебора для машины неизмеримо выше, чем для человека. Применение перебора позволяет найти такие варианты, до которых без компьютера дойти практические невозможно. Суть метода Монте-Карло заключается в следующем: процесс описывается математической моделью с использованием генератора случайных величин, модель многократно обсчитывается, на основе полученных данных вычисляются вероятностные характеристики рассматриваемого процесса. Например, чтобы узнать методом МонтеКарло, какое в среднем будет расстояние между двумя случайными точками в круге, нужно взять координаты большого числа случайных пар точек в границах заданной окружности, для каждой пары вычислить расстояние, а потом для них посчитать среднее арифметическое. Сканирование – метод, близкий к перебору, но применяемый к непрерывным функциям. Рассмотрим для примера одномерное сканирование – случай, когда ищется максимум функции от одного фактора (как я уже говорил, поиск минимума осуществляется точно так же). Будем считать, что мы задались пределами изменения фактора х от а до b. Здесь а и b – ограничения, которые можно установить в любой реальной задаче: никогда не бывает так, что мы может задать любые, ничем не ограниченные значения х. Таким образом имеется интервал [а, b], на котором мы хотим отыскать экстремум целевой функции; его называют интервалом неопределенности. При этом практически нам не нужно определять точку экстремума абсолютно точно. Достаточно сильно сузить интервал неопределенности. Например, если мы узнаем, что оптимальная температура, соответствующая максимуму целевой функции, заключена в пределах от 380 до 381 К, то большая точность не нужна. В промышленных условиях вряд ли удастся регулировать температуру с точностью выше 1 К. Итак, в одномерном случае задача поиска экстремума сводится к сужению интервала неопределенности. Методом сканирования эта задача решается следующим образом. Выбираем целое число q - число значений целевой функции, которое придется рассчитывать. Находим интервал Δx : Откладываем от точки а до точки b интервалы Δх (рис. 7.4). Концы каждого интервала назовем узлами; на рис. 7.4 каждый узел обозначен крестиком. Рис. 7.4. Поиск экстремума сканированием: a, b – границы интервала неопределенности В каждом узле рассчитываем F(х) (см. точки на рис. 7.4). Теперь мы можем принять за максимум наибольшее из полученных значений – на рисунке это 4-я точка слева. К концу расчета интервал неопределенности δ составит 2Δх: истинный максимум может лежать либо справа, либо слева от полученной наилучшей точки (штрихи на рис. 7.4). Таким образом, Формула (7.21) определяет эффективность метода. При сканировании для достижения достаточно малого значения δ величина q должна быть велика. Метод малоэффективен, но удобен для первоначального исследования функции, поскольку дает возможность представить ее вид на всем отрезке, установить число экстремумов и их локализацию. Переменный шаг. Унимодальность. Более эффективно сканирование с переменным шагом: сократив интервал неопределенности, мы продолжаем поиск внутри этого интервала, уменьшая в свою очередь Δх. Например, двигаясь на рис. 7.4 от а к b и дойдя до 5-й слева точки, можно двинуться в обратном направлении меньшими шагами; затем эту процедуру можно продолжить, снова двигаясь вправо и снова уменьшив шаги и т.д. Такой вариант часто называют методом тяжелого шарика (если ищется минимум, то движение точек по кривой функции похоже на скатывание шарика в ложбину, когда он раз за разом проскакивает нижнее положение, колеблясь около него и постепенно приближаясь к нему). Многомерное сканирование. Метод неэффективен, но универсален. Направленный поиск. Обучение алгоритма. Сканированием можно исследовать функции более чем одного фактора. Так, участок на плоскости (факторное пространство для двух факторов) можно покрыть сетью узлов и таким образом исследовать поведение функции на этом участке. В принципе это возможно в любом n-мерном пространстве, но по мере увеличения n резко растет число необходимых расчетов и падает эффективность метода. Другие методы поиска более эффективны, но не обладают той универсальностью, которой отличается сканирование. Их эффективность связана с тем, что это методы направленного поиска, в которых не просто исследуется область факторного пространства, а происходит продвижение в этом пространстве в сторону искомого экстремума. Уже описанное выше сканирование с переменным шагом означает направленность поиска: вблизи экстремума прекращается дальнейшее движение вдоль оси х и начинается сгущение точек около экстремума. Направленность поиска требует соблюдения некоторых условий, ограничивающих применимость методов. Прежде всего направленный поиск дает надежный результат, если функция унимодальна. Наиболее просто (хотя и не вполне строго) унимодальную функцию можно определить так. В допустимой области она имеет только один экстремум нужного знака (один максимум, если ищем максимум, или один минимум в противном случае). Например, на рис. 7.5 функция 1 унимодальна. Функция 2 унимодальна, если ищем максимум, и неунимодальна при поиске минимума (два минимума: при х = а и при х = b). Функция 3 неунимодальна. Рис. 7.5. Графики унимодальных и неунимодальных функций Глобальность. Одномерная и многомерная оптимизация. Методы направленного поиска способны привести в точку одного из экстремумов, но не позволяют установить, единственный ли это экстремум, а если известно, что не единственный, то в какой экстремум мы попали: глобальный (экстремальный для всей области) или локальный (другие точки могут оказаться выше в случае максимума или ниже для минимума). Если при решении задачи оптимизации появится подозрение, что мы встретились с неунимодальностью, можно грубо исследовать функцию сканированием и выделить область глобального экстремума. Еще одно важное свойство функции F, учитываемое при выборе метода поиска, – это число факторов. Здесь различаются два основных случая. Первый, когда F зависит только от одного фактора, F = F(x): тогда говорят об одномерном поиске. Второй, когда факторов больше одного, – многомерный поиск. Причем почти все методы многомерного поиска принципиально применимы при любом числе факторов n > 1, тогда как при n = 1 используются иные, одномерные, методы. Лишь немногие методы, как, например, сканирование, применимы и для одномерного, и для многомерного поиска Локальная минимизация. Обратная задача моделирования как частный случай оптимизации. Идентификация структурная и параметрическая. Модель состояния и модель наблюдения. (какая-то жесть, думаю, это не столь важная инфа:D) Философия применения модели наблюдения как оболочки структурной модели состояния. Интервал неопределённости. Шаг поиска. Точность. Правила останова. Одномерная (однофакторная) оптимизация. Требования к критерию оптимизации: численная непрерывность и дифференцируемость, унимодальность. Метод дихотомии. Ход процесса. Правило выбора направления и интервала неопределенности. Правило останова. Сходимость. Правило останова, связь с вариационным исчислением. Интервал неопределенности. Эффективность и число шагов. Ознакомление Как и при описании сканирования, будем искать максимум на отрезке [а, b], показанном на рис. 7.6. Для этого разделим отрезок пополам – на рисунке точка л (левая). Рассчитаем значение F(л) в этой точке. Пока еще ничего нельзя сказать об экстремуме, кроме того, что он принадлежит нашему отрезку. Рис. 7.6. График поиска максимума методом дихотомии Выберем малое приращение фактора, равное ε, и поставим на отрезке правую точку п = л + ε. Рассчитаем F(п). Поскольку F(л) > F(п), как изображено на рис. 7.6, можно утверждать, что если F(x) унимодальна, то максимум находится в левой половине отрезка. Теперь отбросим правую половину отрезка (на ней максимума нет). Для этого правый конец (точку b) перенесем в точку л и обозначим ее буквой b (такая операция переименования не вполне привычна для традиционной математики, но в алгоритмических языках она чрезвычайно распространена). На рис. 7.6 этот перенос показан стрелкой. Разумеется, при F(л) < F(п) в точку л мы перенесли бы точку а. Можно перенести конец отрезка и в точку п, но так как л и п близки, то это почти одно и то же. После того как правый конец отрезка перенесен, задача вернулась к исходным условиям: задан отрезок от а до b, на котором нужно найти максимум. Поэтому проводится следующий цикл расчета, ничем не отличающийся от предыдущего, кроме значения b. Снова делим пополам отрезок, ставим вспомогательную точку на расстоянии ε, переносим в середину либо правый, либо левый конец. Такой алгоритм (расчет слагается из одинаковых циклов, различающихся лишь начальными условиями) называют итерационным. В принципе итерации можно проводить до бесконечности: делить пополам все меньшие отрезки. Поэтому в любом итерационном алгоритме нужно задать правило останова, определяющее, когда можно прекращать расчет, считая, что полученная точность уже достаточна. Например, можно остановить итерации, когда интервал неопределенности окажется не больше ε: Метод золотого сечения (0.382, 0.618). Правило выбора направления и интервала неопределённости. Отбрасывание «лишней» из 4 точек. Правило останова. Пропорция золотого сечения (деления отрезка в среднем и крайнем отношении) определяется так. Отрезок длины l делится на две части m и l – m так, чтобы меньшая часть относилась большей, как большая ко всему отрезку: Рис. 7.7. График поиска максимума методом золотого сечения Рассмотрим опять отрезок [а, b], на котором нужно найти максимум (рис. 7.7). Поиск максимума начинаем с того, что делим отрезок слева и справа в соответствии с пропорцией золотого сечения и получаем точки л и п. Расстояние от а до л составляет 0,382 (b – а), от а до п 0,618(b – а). В этих точках рассчитаем значения F. Как и в методе дихотомии, здесь имеем две точки л и п, но расстояние между ними не мало и вероятность того, что точка экстремума попадет между ними, достаточно велика. Поэтому, например, если F(п) > F(л) (см. рис. 7.7), то нельзя сказать, в какой из трех частей отрезка окажется максимум – он может быть и в средней части отрезка (левая штриховая линия на рисунке), и в правой (правая штриховая линия). Но в левой части (мы приняли, что функция унимодальна) максимума быть не может. Поэтому можно ее отбросить – перенести левый конец отрезка в точку л, назвав ее а (левая стрелка). Теперь задача как будто вернулась к исходной формулировке: найти максимум на отрезке [а, b]. Но на этом отрезке уже есть точка (точка п, см. рис. 7.7), в которой рассчитано значение функции, причем благодаря свойству (7.24) эта точка, отсекавшая от предыдущего большего отрезка справа ~38,2%, отсекает от нового, уменьшенного отрезка справа ~61,8%, т. е. и на новом отрезке она является точкой золотого сечения. Теперь, на новом этапе расчета мы можем назвать ее л (см. правую стрелку на рис. 7.7) и поставить на уменьшенном отрезке не две точки для расчета F, а только одну – правую (на рис. 7.7 обозначена треугольником). Таким образом, на каждом этапе расчета, кроме самого первого, мы должны рассчитывать F только в одной точке, что повышает эффективность метода. В качестве правила останова можно воспользоваться формулой (7.22). Эффективность метода определяется следующим образом. После двух первых расчетов F и после каждого последующего остающийся интервал неопределенности составляет 0,618 предыдущего. Тогда при q расчетах целевой функции При q > 4 эффективность метода золотого сечения выше, чем метода дихотомии; при небольших q, порядка 10 – 20, эффективность обоих методов близка, но при q > 20 метод золотого сечения становится заметно эффективнее. Таким образом, если не нужно очень точно фиксировать абсциссу оптимума, то можно пользоваться любым из этих методов. Если нужна высокая точность (или если каждый расчет громоздок), то предпочтительнее метод золотого сечения. Впрочем, при малых q часто целесообразно ограничиться сканированием. Многомерная (многофакторная) оптимизация. Классификация методов включает следующие основные альтернативы: градиентные и прямого поиска, управление шагом и направлением регуляризированное или стохастическое, без моделирования поведения целевой функции и с применением такового, но встречаются и более детализированные варианты. Метод покоординатного спуска (Гаусса-Зейделя). Ход процесса. Управление шагом поиска. Правило останова. Правило останова – правило, применяемое для вынесения решения, нужны ли дальнейшие эксперименты. Оно определяет, когда можно прекращать расчет, считая, что полученная точность уже достаточна. Метод покоординатного спуска. Выбираем координаты начальной точки поиска х1Н и x2Н, т. е. те значения х1 и х2, от которых мы начнем искать оптимум, единичные приращения обоих факторов (шаги) Н1 и Н2, а также малые приращения факторов ε1 и ε2. Выбор всех этих величин определяется физическим смыслом задачи и той информацией о ней, которой мы располагаем заранее. Рис. 7.8. График движения в пространстве факторов при покоординатном спуске Рассчитываем значение F(x1Н , x2Н) в точке 1 (рис. 7.8). Далее, не меняя величины х2, начинаем двигаться вдоль оси х1, давая на каждом шаге этому фактору приращение H1 (или –Н1, в зависимости от того, при движении в какую сторону будет наблюдаться рост F ). На каждом шаге – в точках 2, 3, 4 и т. д. – проводится расчет F. Шаги продолжаются до тех пор, пока продолжается рост F. Неудачными будем считать те шаги, на которых получено значение F меньшее, чем на предыдущих шагах (на рисунке они обозначены крестиками). После первого неудачного шага (точка 6) возвращаемся в предыдущую точку (в данном случае в точку 5), фиксируем величину х1 и начинаем изменять х2, давая ему приращения Н2 или –Н2 (точки 7, 8, 9, 10 ). Затем снова движемся вдоль оси х1 (точки 11, 12, 13 ), снова меняем направление (точки 14, 15 ) и т. д. На рис. 7.8 изображена ситуация, когда из точки 12 двигаться некуда: во всех окружающих точках (9, 13, 14, 15 ) значение F меньше, чем в данной. Это значит, что мы уже приблизились к максимуму и прежние крупные шаги из точки 12 переносят нас через него. Поэтому уменьшаем шаги (например, вдвое – см. точку 16 ) и продолжаем поиск уменьшенными шагами. Уменьшение шага может производиться неоднократно. Но в тот момент, когда эти шаги оказываются меньше, чем соответственно ε1 и ε2, логично считать, что максимум зафиксирован достаточно точно и можно закончить расчет, приняв лучшую точку за оптимум. Если факторов больше двух, то после движения вдоль осей х1 и х2 производится движение вдоль осей х3, х4 и т. д. и лишь затем снова начинается движение вдоль х1. В описанном варианте движение вдоль каждой оси осуществляется так же, как при сканировании. Если нужна большая точность определения оптимальных значений xi, можно поступать и по-иному: например, организовывать такое движение, как поиск методом золотого сечения. Метод градиента (Ньютона-Рафсона, крутого восхождения-спуска). Численные частные производные. Ход процесса. Управление шагом поиска. Правило останова. Метод градиента. Существует много вариантов этого метода. Рассмотрим простейший из них. Подробно опишу также лишь случай двух факторов. Как и в методе покоординатного спуска, вначале выберем координаты исходной точки х1Н и х2Н , шаги H1 и Н2 и малые приращения ε1 и ε2. Движение к оптимуму начнем не вдоль какой-либо оси координат, а в направлении градиента (если ищем минимум, то в противоположном градиенту направлении). Поскольку Н1 и Н2 приняты за единичные приращения координат, формула градиента получит вид (полужирный шрифт означает, что выделенные величины – векторы, и сложение ведется как векторное): Ясно, что для расчета направления градиента необходимо знать частные производные целевой функции по факторам. Для расчета производных проводится вспомогательная серия расчетов (см. рис. 7.9). Около начальной точки 1 ставятся две вспомогательные точки: 1' на расстоянии ε1 вдоль оси х1 и 1'' на расстоянии ε2 вдоль оси х2, и в них рассчитывается функция F. Производные находим по формулам Дальше можно действовать по-разному. Можно определить производные в новой точке i + 1, найти новое направление градиента, сделать шаг и т. д. Но чаще поступают иначе. Если шаг оказался удачным, т. е. если Fi+1 > Fi (при поиске максимума), то делают следующий шаг в том же направлении, подставляя в формулу (7.29) ранее найденные значения производных. Практически наверняка это будет уже не направление градиента: его направление в разных точках пространства факторов – разное, если только функция F не является линейной. Но можно надеяться, что еще один шаг в прежнем направлении снова даст приращение F нужного знака, хотя и не максимально возможное (так как от градиента мы отклонились). Зато мы сэкономим на том, что не будем лишний раз рассчитывать производные. Если и этот шаг удачен, шагнем еще раз и т. д. Рис. 7.9. Схема расчетов в методе градиента Рис. 7.10. Схема расчета после неудачного шага Что делать, когда шаг неудачен? Очевидно, поверхность настолько искривлена, что данное направление перестало вести нас вверх, мы «перескочили» через ту окрестность предыдущей точки, в которой функция возрастала. Поэтому в таком случае обычно уменьшают шаг, например вдвое. Теперь, если уменьшенный шаг в том же направлении будет удачен, нет смысла делать еще шаг, поскольку он приведет в «плохую» точку (см. рис. 7.10, а : крестик – неудачный шаг, (i + 2) – точка половинного шага). В этом случае около точки (i + 2) поставим вспомогательные точки для расчета производных по формуле (7.27), найдем новое направление градиента и двинемся по нему (на рис. 7.10 вспомогательные точки – черные кружки, новое направление градиента – стрелка). Если же и уменьшенный шаг не приведет в «хорошую» точку (рис. 7.10, б), то вернемся в точку i и будем в ней искать направление градиента. Движение продолжаем до тех пор, пока шаги не станут очень малыми. Уменьшение шагов объясняется двумя причинами: первая – неоднократным уменьшением в тех случаях, когда большой шаг оказывался неудачным; вторая – это принципиально важнее, – то, что вблизи оптимума производные близки к нулю и формула (7.29) дает уже очень малые приращения. Для останова вычислений можно использовать момент, когда оба приращения Δxij окажутся меньше, чем соответствующие малые величины εj. Метод Розенброка. Форма поверхности отклика целевой функции приближенно моделируется зависимостью второго порядка по факторам (параболоидом). Ход процесса. Управление шагом поиска. Правило останова.*под большим вопросов Метод вращающихся координат (метод Розенброка). Суть метода состоит во вращении системы координат в соответствии с изменением скорости убывания целевой функции. Новые направления координатных осей определяются таким образом, чтобы одна из них соответствовала направлению наиболее быстрого убывания целевой функции, а остальные находятся из условия ортогональности. Идея метода состоит в следующем (рис. 7.6). Из начальной точки х[0] осуществляют спуск в точку х[1] по направлениям, параллельным координатным осям. На следующей итерации одна из осей должна проходить в направлении y1 = х[1] - х[0], а другая - в направлении, перпендикулярном к у1. Спуск вдоль этих осей приводит в точку х[2] , что дает возможность построить новый вектор х[2] - х[1] и на его базе новую систему направлений поиска. В общем случае данный метод эффективен при минимизации овражных функций, так как результирующее направление поиска стремится расположиться вдоль оси оврага. Алгоритм метода вращающихся координат состоит в следующем. 1. Обозначают через р1[k], ..., рn[k] направления координатных осей в некоторой точке х[k] (на к-й итерации). Выполняют пробный шаг h1 вдоль оси р1[k], т. е. x[kl] = x[k] + h1p1[k]. Если при этом f(x[kl]) < f(x[k]), то шаг h умножают на величину α > 1; Если f(x[kl]) > f(x[k]), - то на величину (-α), 0 < | α | < 1; x[kl] = x[k] + α h1p1[k]. Полагая h1 = а1 .получают x[kl] = x[k] + a1p1[k]. 2. Из точки х[k1] выполняют шаг h2 вдоль оси р2[k]: x[k2] = x[k] + a1p1[k] + h2p2[k]. Повторяют операцию п. 1, т. е. x[k2] =x[k] + а1р1[k] +а2p2[k]. Эту процедуру выполняют для всех остальных координатных осей. На последнем шаге получают точку х[kn] = х[k+1] = х[k] + 3. Выбирают новые оси координат p1[k+1], …, рn[k+1]. В качестве первой оси принимается вектор р1[k+1] = x[k+l] - x[k]. Остальные оси строят ортогональными к первой оси с помощью процедуры ортогонализации Грама - Шмидта. Повторяют вычисления с п. 1 до удовлетворения условий сходимости. Коэффициенты α подбираются эмпирически. Хорошие результаты дают значения α = 0,5 при неудачных пробах (f(x[ki]) > f(x[k])) и α = 3 при удачных пробах (f(x[ki]) < f(x[k])). Метод Розенброка ориентирован на отыскание оптимальной точки в каждом направлении, а не просто на фиксированный сдвиг по всем направлениям. Величина шага в процессе поиска непрерывно изменяется в зависимости от рельефа поверхности уровня. Сочетание вращения координат с регулированием шага делает метод Розенброка эффективным при решении сложных задач оптимизации. Например, он эффективен для «овражных» функций, т.к. после спуска «на дно оврага» можно повернуть координаты и следовать к минимуму «по дну оврага». Такие «овражные» функции также получили название функции Розенброка. Функции этого типа часто используют для оценки эффективности различных методов отыскания экстремума. Экспериментальный поиск оптимума. Влияние ошибок измерений на выбор шага поиска. Применение планов 1 и 2 порядка. Применение аппроксимации полиномами. Наиболее сложен для оптимизации случай, когда мы не знаем вида целевой функции. В этом случае единственная возможность – находить оптимум экспериментально. В принципе здесь можно применять любой из рассмотренных методов (дитохомия, золотое сечение), но при этом приходится учитывать ряд дополнительных обстоятельств. Во-первых, вследствие наличия случайных ошибок опытные точки нельзя располагать слишком близко одну к другой. В противном случае значения критерия оптимальности, полученные в соседних точках, окажутся неразличимыми: различия в величине критерия (малые, потому что точки близки) будут значительно меньше уровня ошибки, вследствие чего не удастся опровергнуть гипотезу о равенстве этих значений. Во-вторых, в эксперименте гораздо острее, чем в расчете, стоит проблема эффективности поиска. Эксперимент почти всегда дороже, чем единичный расчет целевой функции. Расчетная задача, где придется 1000 раз рассчитать F, может оказаться не очень большой по объему. Эксперимент же по отыскиванию оптимума, требующий 100 опытов, уже очень велик. В-третьих, при экспериментальной оптимизации характер зависимости F от факторов, как правило, бывает проще, чем при расчетной. Это объясняется тем, что ошибки опытов «сглаживают рельеф» целевой функции. Таким образом, в эксперименте обычно можно работать с простейшими математическими моделями – чаще всего с многочленами 1-го или 2-го порядков. Применительно к планированию эксперимента метод покоординатного спуска обычно называют методом Гаусса – Зайделя. Его главное преимущество – простота. Каждое движение (сканирование) вдоль одной из осей координат означает, что от опыта к опыту изменяется только один фактор и влияние этого фактора получается в ясной форме однофакторной зависимости. Его недостаток – малая эффективность, присущая однофакторному планированию эксперимента (см. разд. 2.4). Поэтому методом Гаусса – Зайделя в эксперименте пользуются не часто. Казалось бы, отмеченная выше простота математических моделей, встречающихся в экспериментальной оптимизации, открывает еще одну возможность. Опишем целевую функцию многочленом. Ясно, что многочлен 1-й степени не может описать зависимость, имеющую экстремум. Более того, и добавление взаимодействий не позволяет этого сделать. Тогда используем многочлен 2-й степени. Реализуем в интересующей нас области план 2-го порядка. Получив оценки параметров многочлена, легко определить экстремум на основе уравнений (7.5). Однако такой способ отыскания экстремума крайне неточнен. Исходная область пространства факторов всегда достаточно велика, и в этой большой области описание целевой функции многочленом 2-го порядка неадекватно, поскольку этот многочлен – лишь приближенное представление неизвестной нам «истинной» функции. Кроме того, экспериментальные точки в этом случае располагаются нерационально: в большинстве своем они попадают в части области, далекие от экстремума и поэтому неинтересные для исследователя. Понятие об идентифицируемости как возможности определения искомых параметров модели и характеристик полученных оценок: однозначности и точности. Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. Метод Бокса –Уилсона. (на всякий случай) Он состоит в следующем. Сначала ставится одна или несколько серий опытов, цель которых – приблизиться к оптимуму по градиенту функции, а затем вблизи экстремума ставится план 2-го порядка и оптимум отыскивают так, как описано выше. В планировании эксперимента градиентный метод движения к оптимуму называют крутым восхождением. Отличия от метода, описанного в разд. 7.3, обусловлены ошибками опытов. По этой причине нельзя находить частные производные так, как там указано: в формулах (7.27) приращения ε должны быть малы; при малых расстояниях между точками слишком сильно скажутся ошибки опытов и оценка направления градиента будет очень сильно отклоняться от истинного направления. Поэтому поступим так. Вокруг исходной точки как центра построим факторный эксперимент 2р или дробный факторный эксперимент. Зависимость отклика от факторов опишем многочленом 1-й степени (в дальнейшем, как и в разд. 2.4, будем обозначать критерий оптимальности, он же отклик, буквой у): Тогда частные производные равны соответствующим коэффициентам регрессии: С учетом этого, а также того, что за единичный шаг в направлении каждой оси uj (uj выражено в размерных, некодированных, так называемых натуральных единицах) естественно принять интервал варьирования δj , формула (7.29) примет вид Здесь m – множитель, регулирующий длину шага: шаг должен быть не слишком мал, иначе движение будет очень медленным, но и не слишком велик, а то можно быстро уйти в область, где направление градиента совсем иное. Удачный выбор значения m обычно связан с достаточным опытом в применении метода. В качестве разумной, хотя зачастую и не самой лучшей, могу рекомендовать такую оценку: Выражение в знаменателе – наибольшая из абсолютных величин коэффициентов регрессии, за исключением свободного члена. В таком случае шаг по оси наиболее сильно влияющего фактора равен интервалу варьирования, по остальным – соответственно меньше. Отмечу еще одну особенность расчета по уравнению (7.32). Не следует стремиться получать значения приращений факторов со слишком большой точностью. Наоборот, значения, найденные по формуле (7.32), желательно округлять так, чтобы в опытах задавались удобные значения факторов. Нецелесообразно изменять от опыта к опыту температуру на 4,263°, куда удобнее – на 4,25° или даже на 4°. Дело в том, что направление градиента очень чувствительно к значениям принимаемых при построении плана интервалов варьирования. Но мы реально всегда задаем эти интервалы не на основе серьезной теории, а весьма приблизительно – обычно ориентируясь на привычные круглые значения. Практически никогда мы не можем утверждать, что интервал варьирования температуры 10° с точки зрения какой-то теории лучше, чем интервал 11,18°. Но расчет по формуле (7.33) даст при принятии этих интервалов существенно разные значения. Поэтому, если мы округляем шаги по осям в крутом восхождении, у нас нет никаких причин думать, что мы замедляем (равно как и ускоряем) движение к экстремуму. Движение по направлению крутого восхождения продолжается до тех пор, пока у возрастает (либо убывает, если мы ищем минимум). После этого либо ставят новый факторный эксперимент и находят новое направление градиента, либо переходят к плану 2-го порядка, как было рассказано выше.