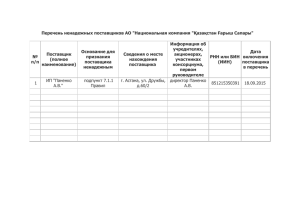
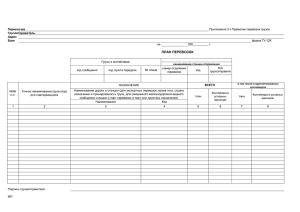
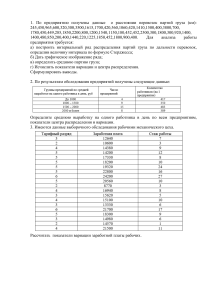
АНАЛИЗ ТРАНСПОРТНОЙ ЗАДАЧИ ЗАКРЫТОГО ТИПА
Радченко Н.Д.
Белорусский государственный университет информатики и радиоэлектроники1
г. Минск, Республика Беларусь
Касабуцкий А.Ф. – доцент
Транспортная задача линейного программирования получила широкое распространение в практическом применении на транспорте.
Целью данной задачи является разработка рациональных путей и способов транспортировки товаров, устранение некорректных
или повторных перевозок.
Целью работы является анализ транспортных задач закрытого типа и их реализация при
решении практической задачи. Среди задач линейного программирования особо выделяется
транспортная задача. Смысл заключается в отыскании такого плана перевозок продукции с m складов
в пункт назначения n который потребовал бы минимальных затрат. Через 𝑐𝑖𝑗 обозначим стоимость
перевозки одной единицы груза из 𝑖-го склада к 𝑗-му потребителю. При этом 𝑎𝑖 означает запас груза
у 𝑖-го склада, а 𝑏𝑗 – потребность соответствующего потребителя. Общая стоимость перевозки
вычисляется как сумма всех затрат на перевозку товара от каждого склада к каждому потребителю.
Если выражаться на языке формул, то постановка выглядит так:
𝑚
𝑛
∑ ∑ 𝑐𝑖𝑗 𝑥𝑖𝑗 (𝑚𝑖𝑛)
𝑖=1 𝑗=1
(1)
при следующих ограничениях:
𝑛
∑ 𝑥𝑖𝑗 = 𝑎𝑖 ,
𝑗=1
𝑚
∑ 𝑥𝑖𝑗 = 𝑏𝑖 ,
𝑖=1
𝑥𝑖𝑗 ≥ 0, 𝑐𝑖𝑗 ≥ 0, 𝑎𝑖 ≥ 0, 𝑏𝑖 ≥ 0,
{ 𝑖 = 1, 2, … , 𝑚; 𝑗 = 1, 2, … , 𝑛.
(2)
В условии (1) числа 𝑐𝑖𝑗 обозначают тарифы перевозок единицы груза от 𝑖-го поставщика к 𝑗-му
потребителю, 𝑥𝑖𝑗 – объемы перевозок от 𝑖-го поставщика к 𝑗-му потребителю. Первое равенство
условия (2) означает, что все запасы грузов вывезены. Второе равенство условия (2) означает, что
все потребности потребителей удовлетворены.
Существует две разновидности транспортной задачи – открытая и закрытая. Закрытая задача
характеризуется тем, что суммарная потребность всех потребителей равна суммарным запасам всех
складов. То есть, весь товар на всех складах будет реализован полностью. Формула:
𝑚
𝑛
∑ 𝑎𝑖 = ∑ 𝑏𝑖
𝑖=1
𝑗=1
(3)
В открытой задаче суммарная потребность и суммарные запасы не совпадают. Формула выше
подходит только для транспортных задач закрытого типа.
Данные задачи удобно записывать в виде распределительной таблицы, или таблицы поставок.
Пункты
отправления
𝐴1
𝐵1
𝑐11
𝑥11
…
…
Пункты назначения
…
…
𝐵𝑗
…
…
𝑐1𝑗
…
…
𝑥1𝑗
…
…
…
𝐴𝑖
…
…
𝐴𝑚
…
𝑥𝑚𝑗
…
𝑏1
𝑐𝑖𝑛
…
…
…
𝑐𝑚𝑛
𝑥𝑚𝑛
…
𝑏𝑗
𝑎𝑖
𝑥𝑖𝑛
…
…
𝑐𝑚𝑗
…
…
…
…
…
𝑥𝑚1
Потребности
…
…
…
𝑐𝑚1
…
𝑥𝑖𝑗
…
…
𝑎1
𝑥1𝑛
…
…
𝑐𝑖𝑗
…
𝑥𝑖1
𝑐1𝑛
…
…
…
𝑐𝑖1
…
…
Запасы
𝐵𝑛
𝑎𝑚
𝑏𝑛
Решение транспортной задачи начинается с нахождения опорного плана. Для этого существуют
различные способы. Например, способ северо-западного угла, метод минимального элемента,
метод аппроксимации Фогеля, метод потенциалов, метод дифференциальных рент. Рассмотрим, так
называемый способ северо-западного угла. Сущность его состоит в следующем. Будем распределять
груз в таблице, начиная с загрузки левой верхней, условно называемой «северо-западной», клетки
(1,1), двигаясь затем от нее по строке вправо или по столбцу вниз. В клетку (1,1) занесем меньшее из
чисел a1, b1 то есть 𝑥11 = min(𝑎1 , 𝑏1 ). Если a1> b1, то x11= b1 и первый потребитель B1 будет полностью
удовлетворен. В дальнейшем 1-й столбец таблицы в расчет не принимается: в нем переменные xi1 для
𝑖 = ̅̅̅̅̅̅
2, 𝑚 . Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1,2) меньшее из
чисел (𝑎1 − 𝑏1) и 𝑏2 , то есть 𝑥12 = min(𝑎1 − 𝑏1 , 𝑏2 ). Если (𝑎1 − 𝑏1 ) < 𝑏2 , то запасы первого поставщика
исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к
аналогичному распределению запаса груза второго поставщика.
Если 𝑏1 > 𝑎1 , то 𝑥11 = min(𝑎1 , 𝑏1 ) = 𝑎1 . При этом запас первого поставщика будет исчерпан, а
̅̅̅̅̅
потому 𝑥1𝑘 = 0 для 𝑘 = 2,
𝑛. Первая строка из дальнейшего рассмотрения исключается. Переходим к
распределению запасов второго поставщика. В клетку (2,1) заносим наименьшее из чисел (𝑎2 , 𝑏1 − 𝑎1 ).
Заполнив таким образом клетку (1,2) или (2,1), переходим к загрузке следующей клетки по второй
строке либо по второму столбцу. Процесс распределения по второй, третьей и последующим строкам
(столбцам) производится аналогично распределению по первой строке или по первому столбцу до тех
пор, пока не исчерпаются ресурсы. Последней заполняется клетка (𝑚, 𝑛).
Пример:
B1
A1
B2
10
18
5
6
9
𝒂𝒊
48
8
6
5
30
7
27
8
20
B3
8
27
B4
3
A2
6
7
A3
8
7
10
9
A4
7
B5
5
8
12
4
6
6
20
𝒃𝒋
18
27
42
12
26
Список использованных источников:
1. Е. Г. Гольштейн, Д. Б. Юдин «Задачи линейного программирования транспортного типа», Москва, 1993.
2. И. Л. Акулич, В. Ф. Стрельчонок «Математические методы и компьютерные технологии решения
оптимизационных задач», Рига, 2000.
3. Моисеев Н.Н., Иванов Ю.П., Столярова Е.М. Методы оптимизации. - М.; Наука, 1978г.
4. Бронштейн И.Н., Семендяев К.А. Справочник по математике. - М.; Наука, 1986г.