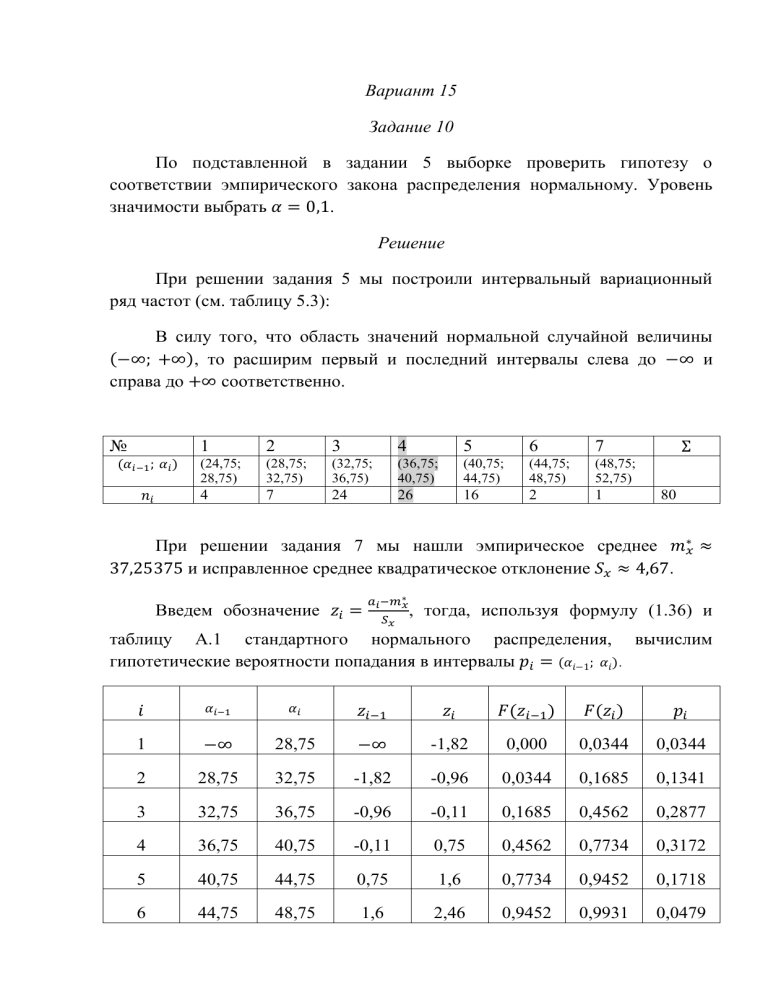
Вариант 15 Задание 10 По подставленной в задании 5 выборке проверить гипотезу о соответствии эмпирического закона распределения нормальному. Уровень значимости выбрать 𝛼 = 0,1. Решение При решении задания 5 мы построили интервальный вариационный ряд частот (см. таблицу 5.3): В силу того, что область значений нормальной случайной величины (−∞; +∞), то расширим первый и последний интервалы слева до −∞ и справа до +∞ соответственно. № (𝛼𝑖−1 ; 𝛼𝑖 ) 𝑛𝑖 1 2 3 4 5 6 7 (24,75; 28,75) (28,75; 32,75) (32,75; 36,75) (36,75; 40,75) (40,75; 44,75) (44,75; 48,75) (48,75; 52,75) 4 7 24 26 16 2 1 Σ 80 При решении задания 7 мы нашли эмпирическое среднее 𝑚𝑥∗ ≈ 37,25375 и исправленное среднее квадратическое отклонение 𝑆𝑥 ≈ 4,67. Введем обозначение 𝑧𝑖 = 𝑎𝑖 −𝑚𝑥∗ 𝑆𝑥 , тогда, используя формулу (1.36) и таблицу А.1 стандартного нормального распределения, вычислим гипотетические вероятности попадания в интервалы 𝑝𝑖 = (𝛼𝑖−1 ; 𝛼𝑖 ). 𝑖 𝛼𝑖−1 𝛼𝑖 𝑧𝑖−1 𝑧𝑖 𝐹(𝑧𝑖−1 ) 𝐹(𝑧𝑖 ) 𝑝𝑖 1 −∞ 28,75 −∞ -1,82 0,000 0,0344 0,0344 2 28,75 32,75 -1,82 -0,96 0,0344 0,1685 0,1341 3 32,75 36,75 -0,96 -0,11 0,1685 0,4562 0,2877 4 36,75 40,75 -0,11 0,75 0,4562 0,7734 0,3172 5 40,75 44,75 0,75 1,6 0,7734 0,9452 0,1718 6 44,75 48,75 1,6 2,46 0,9452 0,9931 0,0479 7 +∞ 48,75 +∞ 2,46 0,9931 1,000 0,0069 Вычислим гипотетические частоты интервалов 𝑖 𝛼𝑖−1 ; 𝛼𝑖 ) 1 (−∞; 28,75) 4 0,0344 2,752 2 (28,75; 32,75) 7 0,1341 10,728 3 (32,75; 36,75) 24 0,2877 23,016 4 (36,75; 40,75) 26 0,3172 25,376 5 (40,75; 44,75) 16 0,1718 13,744 6 (44,75; 48,75) 2 0,0479 3,832 7 (48,75; +∞) 1 0,0069 0,552 𝑛𝑖 𝑝𝑖 𝑛𝑝𝑖 Так как гипотетическая частота первого интервала 𝑛𝑝1 = 2,752 < 5, объединим его со вторым. Так как гипотетическая частота шестого интервала 𝑛𝑝1 = 3,832 < 5, объединим его с пятым. Так как гипотетическая частота седьмого интервала 𝑛𝑝7 = 0,552 < 5, объединим его с пятым. После чего вычислим статистику критерия, для этого составим следующую таблицу: i 1 2 3 4 (ai-1; ai) (-…; 32,75) (32,75; 36,75) (36,75; 40,75) (40,65; +...) Сумма ni pi npi ni-npi (ni-npi)^2 ((ni-npi)^2)/npi 11 0,1685 13,48 -2,48 6,1504 0,456261128 24 0,2877 23,016 0,984 0,968256 0,042068822 26 0,3172 25,376 0,624 0,389376 0,015344262 19 0,2266 18,128 0,872 0,760384 0,041945278 80 0,55561949 С учетом того, что количество интервалов разбиения 𝑚 = 4, число оцененных по выборке параметров 𝑠 = 2, то число степеней свободы статистики равно 𝑚 − 𝑠 − 1 = 4 − 2 − 1 = 1. По таблице Г.1 найдем критическое значение 2 𝑋крит = ℎ1−0.1 (1) = ℎ0.9 (1) = 2,7055 В силу того, что 2 𝑋 2 < 𝑋крит , то гипотеза 𝐻0 принимается, т.е. с вероятностью 0,9 можно считать, что выборка изъята из нормального распределения.









