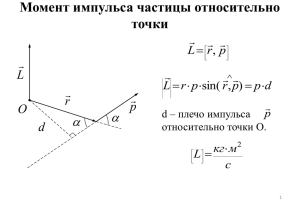
1.3.1 Импульс системы. Закон сохранения импульса системы .......................2 1.4.1 Момент импульса материальной точки. Момент силы. Уравнение моментов. Момент импульса и момент силы относительно оси. ..................3 1.4.2 Момент импульса системы тел. Закон сохранения момента импульса системы. ...............................................................................................................4 1.4.4 Момент инерции тела относительно оси. Основное уравнение динамики вращательного движения твёрдого тела с закреплённой осью вращения. Теорема Штейнера. Моменты инерции некоторых тел. ..............5 1.5.1 Механическая работа. Работа некоторых сил. Мощность......................6 2.1.2 Идея близкодействия. Напряжённость электрического поля. Принцип суперпозиции. Поля точечного и распределенного зарядов. Силовые линии Электрического поля. ..............................................................................7 2.1.3 Поток вектора напряжённости электрического поля. Теорема Гаусса в интегральной и дифференциальной формах. ..................................................8 2.2.2 Электроёмкость уединённого проводника и конденсатора. Электроёмкость конденсаторов различной формы. Соединения конденсаторов. ....................................................................................................9 2.3.2 Закон Ома для однородного проводника и однородной проводящей среды в интегральной и дифференциальной формах. Соединения резисторов. ........................................................................................................10 2.4.2 Индукция магнитного поля движущегося заряда. Закон Био-СавараЛапласа для распределенных и линейных токов. Магнитное поле на оси кругового тока. Магнитный диполь. ................................................................11 2.4.5 Закон Ампера для распределенного и линейного тока. Взаимодействие линейных токов: определение единицы тока-Ампера. Сила, действующая на рамку с током однородном и неоднородном магнитном поле .................................................................................................12 1.3.1 Импульс системы. Закон сохранения импульса системы Импульс системы может быть выражен через скорость ее центра масс. Ее радиус-вектор равен Тогда, скорость центра масс т.е. импульс системы равен произведению массы системы на скорость ее центра масс. Закон сохранения импульса системы В случае отсутствия внешних сил (рассматриваем замкнутую систему) Последнее выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. 1.4.1 Момент импульса материальной точки. Момент силы. Уравнение моментов. Момент импульса и момент силы относительно оси. где М— псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением: Модуль момента силы где, а — угол между r и F; rsin α = / — кратчайшее расстояние между линией действия силы и точкой О — плечо силы. где r — радиус-вектор, проведенный из точки О в точку А; р = mv — импульс материальной точки; L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от Модуль вектора момента импульса Моментом силы относительно неподвижной оси z называется скалярная величина М, равная проекции на эту ось вектора Л/момента силы, определенного относительно произвольной точки О данной оси z. Значение момента М, не зависит от выбора положения точки О на оси z. где, а — угол между векторами г и р; l — плечо вектора р относительно точки О. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью: Уравнение моментов Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса оси z. не зависит от положения точки О на Момент силы Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора г, проведенного из точки О в точку Л приложения силы, на силу F Получим 1.4.2 Момент импульса системы тел. Закон сохранения момента импульса системы. Моментом импульса системы двух тел называют сумму моментов импульсов тел: Где L1 и L2 моменты импульсов рассматриваемых тел относительно точки О, которая выбрана в качестве начала инерциальной системы отсчета. В замкнутой системе момент внешних сил М=0 и dL/dt=0, откуда L = const. (19.4) Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. 1.4.4 Момент инерции тела относительно оси. Основное уравнение динамики вращательного движения твёрдого тела с закреплённой осью вращения. Теорема Штейнера. Моменты инерции некоторых тел. Момент инерции тела относительно оси. Момент инерции тела — мера инертности твердых тел при вращательном движении Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс п материальных точек системы на квадраты их расстоянии до рассматриваемой оси: Основное уравнение динамики вращательного движения твёрдого тела с закреплённой осью вращения. Это уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Можно показать, что если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство Найдем выражение для работы при вращении тела. где J — главный момент инерции тела (момент инерции относительно главной оси). Теорема Штейнера. момент инерции J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела Jс относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, а — угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол точка приложения В проходит путь ds — и работа равна произведению проекции силы на направление смещения на величину смещения: Учитывая модуль момента силы, можем записать где F*r*sin(a) = — момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: Моменты инерции некоторых тел. 1.5.1 Механическая работа. Работа некоторых сил. Мощность. Изменение механического движения тела вызывается силами, действующими на него со стороны других тел. Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работы силы. Работа упругой силы Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол с направлением перемещения, то работа этой силы равна произведению проекции силы на направление перемещения ( точки приложения силы: = Fcos а), умноженной на перемещение Мощность. Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности: Сила может изменяться как по модулю, так и по направлению. Элементарной работой силы F на перемещении dr называется скалярная величина За время dt сила F совершает работу Fdr, и мощность, развиваемая этой силой, в данный момент времени где, а — угол между векторами F и dr; ds = |dr| — элементарный путь; Fs — проекция вектора F на вектор dr. т.е. равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы; N — величина скалярная. Средняя мощность Работа на конечном перемещении Зная мощность силы, можно найти и работу, которую совершает эта сила за промежуток времени t. Единица работы — джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н на пути 1 м (1 Дж = 1 Н • м). Свойства работы 1. cos α = 0 – A = 0 Единица мощности — ватт (Вт): 1 Вт — мощность, при которой за время 1 с совершается работа 1 Дж (1 Вт = 1 Дж/с). cos α < 0 – A < 0 Свойство мощности cos α > 0 – A > 0 2. 1. Работа суммы сил = алгебраической сумме работ, по данному пути. 2. Работа Гравитационной (или Кулоновской) сил cos α = 0 – N = 0 cos α < 0 – N < 0 cos α > 0 – N > 0 Мощность суммарной силы равна 2.1.2 Идея близкодействия. Напряжённость электрического поля. Принцип суперпозиции. Поля точечного и распределенного зарядов. Силовые линии Электрического поля. Согласно теории близкодействия, все электрические явления определяются изменениями полей зарядов, причем эти изменения распространяются в пространстве от точки к точке с конечной скоростью. Теория близкодействия: энергия локализована в поле и носителем энергии в пространстве является поле. Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и равная отношению силы F, действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q: Формула (80.2) выражает принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность Ё результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности Поля точечного и распределенного зарядов Силовые линии Линии, касательные к которым совпадают с направлением вектора E напряженности электрического поля, называются линиями напряженности электрического поля, или силовыми линиями. 2.1.3 Поток вектора напряжённости электрического поля. Теорема Гаусса в интегральной и дифференциальной формах. Элементарный поток вектора напряженности – это физическая величина, равная произведению модуля вектора нормалью к площадке: В данной формуле , площади ΔS и косинуса угла α между вектором и является модулем нормальной составляющей поля . Поток вектора напряженности в случае замкнутой поверхности записывают через криволинейный интеграл по замкнутой поверхности: Теорема Гаусса в интегральной и дифференциальной формах. Эта формула выражает теорему Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной па . В соответствии с принципом суперпозиции , тогда каждый из интегралов, стоящий под знаком суммы, равен следовательно, 2.2.2 Электроёмкость уединённого проводника и конденсатора. Электроёмкость конденсаторов различной формы. Соединения конденсаторов. уединенный проводник, т. е. проводник, который удален от других проводников, тел и зарядов. Электроемкость уединенного проводника — физическая величина, равная отношению электрического заряда уединенного проводника к его потенциалу Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу. В СИ единицей электроемкости является фарад (Ф). Конденсатор состоит на двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы делят на плоские, цилиндрические и сферические. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов между его обкладками: Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 При наличии диэлектрика между обкладками разность потенциалов Подставив (94.6) в (94.1), получим 1. Параллельное соединение конденсаторов. У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна отдельных конденсаторов Если емкости то, согласно (94.1), их заряды равны ПЛОСКИЙ КОНДЕНСАТОР: При наличии диэлектрика между обкладками разность потенциалов между ними где — диэлектрическая проницаемость. Заменяя а заряд батареи конденсаторов Полная емкость батареи получим выражение для емкости плоского конденсатора: ЦИЛИНДРИЧЕСКИЙ КОНДЕНСАТОР: 2. Последовательное соединение конденсаторов. У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи Разность потенциалов между обкладками с линейной плотностью τ = Q/l где для любого из рассматриваемых конденсаторов С другой стороны, Подставив в (94.1), получим выражение для емкости цилиндрического конденсатора: откуда СФЕРИЧЕСКИЙ КОНДЕНСАТОР: Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее. 2.3.2 Закон Ома для однородного проводника и однородной проводящей среды в интегральной и дифференциальной формах. Соединения резисторов. Уравнение (98.1) выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления Учитывая, что в закон Ома (98.1), получим (удельная электрическа проводимость), (напряженность электрического поля в проводнике), можно записать в виде ( плотность тока), формулу Выражение (98.5) — закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Соединения резисторов Последовательное соединение Параллельное соединение 2.4.2 Индукция магнитного поля движущегося заряда. Закон Био-Савара-Лапласа для распределенных и линейных токов. Магнитное поле на оси кругового тока. Магнитный диполь. где j = j(r), dV — элемент объёма, r — соответствует текущей точке при интегрировании На рис. 164, а показаны линии магнитной индукции поля кругового тока В результате обобщения опытных данных был установлен закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v. Этот закон выражается формулой где r — радиус-вектор, проведенный от заряда Q к точке наблюдения М. Согласно выражению (113.1), вектор В направлен перпендикулярно плоскости, в которой расположены векторы v и r. Модуль магнитной индукции (113.1) вычисляется по формуле где, а — угол между векторами v и r. Формула (113.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Закон Био — Савара — Лапласа для проводника с током /, элемент dl которого создает в некоторой точке А индукцию поля dB, записывается в виде где dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током; r — радиус-вектор, проведенный из элемента dl проводника в точку Л поля; r — модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Модуль вектора dB определяется выражением где, а — угол между векторами d/ и г. Для распределённых токов Магнитный диполь Магнитным диполем является небольшая петля с током. Под словом «небольшая» понимают то, что размеры витка с током много меньше, чем геометрические величины, характеризующие размеры петли. Любая петля с током создает магнитное поле, которое можно уподобить электрическому полю от электрического диполя. Магнитный диполь характеризуется магнитным моментом 2.4.5 Закон Ампера для распределенного и линейного тока. Взаимодействие линейных токов: определение единицы тока-Ампера. Сила, действующая на рамку с током однородном и неоднородном магнитном поле Закон Ампера применяется для определения силы взаимодействия двух токов. Cила dF, с которой магнитное поле действует на элемент проводника dl с током, находящегося в магнитном поле, равна Модуль силы Ампера вычисляется по формуле Направление вектора dF может быть найдено, по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца — по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток. Взаимодействие линейных токов: определение единицы тока-Ампера. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. 1 ампер – это такая сила постоянного тока, протекающего по двум прямолинейным, параллельным, бесконечным и очень тонким проводникам, находящимся в вакууме на расстоянии 1 м друг от друга, при которой сила их взаимодействия равна 2· 10-7 H на каждый метр длины. Сила, действующая на рамку с током однородном и неоднородном магнитном поле Если рамку с током поместить в магнитное поле, то она будет поворачиваться, пока ее плоскость не установится перпендикулярно линиям магнитной индукции В. Механический момент М, вращающий рамку, создают две противоположно направленные силы Ампера Fх и F3, действующие на противоположные (вертикальные на рис. 15.7) стороны рамки с током и образующие пару сил, тогда как силы Ампера F2 и F4, действующие на две другие (верхнюю и нижнюю) стороны рамки, компенсируют друг друга, поскольку направлены противоположно и вдоль одной прямой.