МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РФ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
СТАВРОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ
УНИВЕРСИТЕТ
Кафедра информационных систем
КУРСОВОЙ ПРОЕКТ
Дисциплина: «Высокоуровневые методы программирования»
Тема «Высокоуровневое программирование алгоритма численного
интегрирования методом правых прямоугольников»
Вариант 31
Выполнил:
студент 6 курса 5 группы
направления
«Прикладная информатика
(магистр) 09.04.03»
Альталеб Юусиф Зиад
Проверил:
Доцент кафедры
информационных систем,
к.т.н. Герасимов Владимир
Павлович
Дата сдачи__________________
Дата защиты________________
Оценка______________________
Ставрополь, 2019
Содержание
Введение ............................................................................................................... 3
1 Постановка задачи и анализ методов интегрирования ................................... 5
1.1 Спецификации задачи ................................................................................. 5
1.2 Формулировка задачи ................................................................................. 5
1.3 Анализ методов вычислительной математики при интегрировании,
используемых в курсовой работе ..................................................................... 6
1.4 Метод прямоугольников ............................................................................. 7
2 Подготовка данных для Альфа-тестирования ............................................... 11
3 Разработка приложения для численного интегрирования методом правых
прямоугольников на языке Visual Basic for Applications ................................. 14
3.1 Описание методов программирования, примененных в работе ............ 16
3.2 Листинги программы ................................................................................ 17
3.3 Описание программы ................................................................................ 19
Заключение ......................................................................................................... 23
Список используемых источников .................................................................... 24
2
Введение
Профессиональная
деятельность
по
направлению
«Прикладная
информатика» предполагает создание, внедрение, анализ, сопровождение и
эксплуатацию профессионально-ориентированных информационных систем,
связанных с обработкой экономической информации. В профессиональной
подготовке
будущих
специалистов
данного
направления
изучение
дисциплины «Высокоуровневые методы программирования» обеспечивает
уровень подготовленности, необходимый для успешного применения
специальных программных средств при проектировании, создании и
использовании
профессионально-ориентированных
пользовательских
оболочек информационных систем.
Многие экономические задачи, задачи физики, геометрии и многих
других областей человеческой деятельности приводят к необходимости
𝑏
вычислять определенный интеграл вида ∫𝑎 𝑓 (𝑥 )𝑑𝑥 , где f(x) – подынтегральная
функция, непрерывная на отрезке [a; b].
Если интеграл от данной функции не может быть вычислен по формуле
Ньютона-Лейбница, или если функция f(x) задана графически или таблицей,
то для вычисления определенного интеграла применяют приближенные
формулы. Для приближенного вычисления интеграла существуют различные
численные методы, таких как:
метод прямоугольников;
трапеций;
Симпсона и др.
Главная особенность обучения основам численных методов, которая все
отчетливее проявляется в последние годы, связана с интенсификацией
процессов использования различных специализированных математических
пакетов
и
систем
программирования
инструмента решения прикладных задач.
3
вычислительных
методов,
как
Задача курсового проекта – разработать программы численного
интегрирования на языках высокого уровня VBA и VB. В данной работе
рассматривается метод правых прямоугольников.
4
1 Постановка задачи и анализ методов интегрирования
1.1 Спецификации задачи
Разрабатываемая программа должна обладать следующими качествами:
1. Интегрирование заданной функции методом прямоугольников, и
выводить результат;
2. Иметь графический интерфейс, позволяющий вводить исходные
данные, а также визуализировать результаты вычислений.
При написании исходных текстов программы необходимым условием
является использование основных принципов объектно-ориентированного
программирования,
обработки
исключительных
ситуаций,
потоков
выполнения, наличие подключаемых библиотек
1.2 Формулировка задачи
Курсовая
работа
посвящена
разработке
программы
на
языках
программирования высокого уровня VBA и VB, на которых реализован
алгоритм приближенного вычисления определенного интеграла от функции,
имеющей первообразную. В работе для решения поставленной задачи
применяется метод правых прямоугольников, который позволяет:
a) вычислить определенный интеграл от функции:
f(x) = x - Cos(x)
на отрезке [0,5; 2,5]
б) вводить с клавиатуры пределы интегрирования и количество
интервалов разбиения (a, b и n);
в) увидеть результаты вычислений на экране в удобном для восприятия
виде.
Программа должна отвечать следующим требованиям:
a) иметь простой (дружественный) интерфейс;
б) иметь кнопки с четкими характеристиками.
5
Актуальность реализации программы на компьютере объясняется
необходимостью
освоения
магистрантами
современных
методов
программирования для проведения эффективных научных исследований.
1.3 Анализ методов вычислительной математики при интегрировании,
используемых в курсовой работе
Определенный интеграл
b
I
f x dx
(1)
a
с пределами интегрирования a и b можно трактовать как площадь фигуры,
ограниченной ординатами a и b, осью абсцисс x и графиком подынтегральной
функции f x . Обыкновенный определенный интеграл, у которого известна
его первообразная
F x ,
вычисляется по формуле Ньютона-Лейбница
I F a F b . Поэтому для вычисления простых определенных интегралов
достаточно вычислить значение F x .
На практике часто встречаются интегралы, которые не выражаются
через элементарные функции или выражаются очень сложно. Нередко
подынтегральная функция задается таблицей или графиком. В этих случаях
интегралы находятся приближенными методами, которые заключаются в
интерполяции f x на отрезке a, b подходящим полиномом, для которого
интеграл вычисляется по формулам численного интегрирования. Обычно
отрезок a, b разбивается на m частей, к каждой из которых применяется
соответствующая простая формула. Таким образом, получают составные (или
сложные) формулы численного интегрирования. Для данной курсовой работы
предусмотрено рассмотреть три способа численного интегрирования с
помощью метода прямоугольников, криволинейных трапеций и метода
Симпсона (параболических трапеций).
6
1.4 Метод прямоугольников
Промежуток интегрирования a, b делится точками x1 , x2 , , xn1 , xn на n
равных частей; длина каждой
h
ba
.
n
Для единообразия полагаем a x0 , b xn . Через x 1 , x 3 , x 5 , обозначаем
2
2
2
середины участков ( x0 , x1 ), ( x1 , x2 ), ( x2 , x3 ), Полагаем
f ( x0 ) y0 , f ( x1 ) y1 , , f ( xn1 ) yn1 , f ( xn ) yn ;
f ( x 1 ) y 1 , f ( x 3 ) y 3 , f ( x 5 ) y 5 , .
2
2
2
2
2
2
Формулой прямоугольников называются следующие приближенные
равенства:
b
f ( x)dx
a
b
f ( x)dx
a
b
f ( x)dx
a
ba
y0 , y1 ,, y n1 – формула правых прямоугольников.
n
(2)
ba
y1 , y 2 ,, y n1 , y n – формула левых прямоугольников.
n
(3)
ba
y 1 , y 3 ,, y 2 n1 – формула средних прямоугольников.
2
n 2 2
(4)
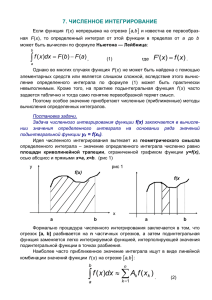
Выражения
(2),
(3),
(4)
дают
площади
ступенчатых
фигур,
изображенных на рисунках 1, 2, 3 соответственно. В большинстве случаев при
данном n формула (4) точнее, чем (2) и (3). С увеличением n точность формул
(2), (3), (4) неограниченно возрастает.
Предельная погрешность формулы (4) составляет:
b a 3 M ,
2
2
24n
где M 2 – наибольшее значение f (x ) в промежутке a, b .
7
Рисунок 1 – Ступенчатая фигура, полученная по методу правых
прямоугольников
Рисунок 2 – Ступенчатая фигура, полученная по методу левых
прямоугольников
Рисунок 3 – Ступенчатая фигура, полученная по методу средних
прямоугольников
Формула (4) наиболее точная, и погрешность по сравнению с формулами
(2) и (3) уменьшается в приблизительно 50 раз. Отметим, что для линейной
8
функции f x kx b формула (4) дает точный ответ, поскольку в этом случае
f x 0 .
Но в работе реализуется метод правых прямоугольников в соответствие
с заданием. Требуемая точность будет достигаться уменьшением шага
дискретизации (увеличением количества отрезков – n). Блок-схема алгоритма
численного интегрирования методом правых прямоугольников приведена на
рисунке 4.
начало
Начало
a, b, n
h = (b-a)/(n-1)
S=0
x=a+h
i = 1, n-1
S = S + x - Cos(x)
x=x+h
Sint = S * h
Sint
Конец
Рисунок 4 - Блок-схема алгоритма численного интегрирования
методом правых прямоугольников
9
Для
предварительного
тестирования
разрабатываемых
программ
принято решение проверить их правильность реализацией алгоритма в
табличном процессоре MS Excel табулированием и построением графика.
10
2 Подготовка данных для Альфа-тестирования
Для этой цели использован табличный процессор MS Excel, который
позволит интегрировать функцию f(x) на отрезке [а, b] с заданным
количеством отрезков n графическим методом с применением численного
метода правых прямоугольников.
Другими словами, интегрирование заданной функции, согласно
варианта
по
списку,
позволяет
разрешить
проблему
с
заданной
погрешностью,. Также необходимо принять во внимание, что в таблице
исходных данных, представленных в таблице 1, где f(a) – значение функции f
в точке а. Вариант задания выбирается, либо в соответствии с номером по
списку учебной группы, либо согласно предпочтению студента.
Таблица 1 - Исходные данные к курсовому проекту
Вариант №
f(x)
[a; b]
f(a)
31
f = x - Cos(x)
0.5; 2.5
-0.377583
Первоначально отметим, что суть метода правого прямоугольника
заключается в том на определенном отрезке можно вычислить приближенное
значение интеграла заданной функции. Для этого, на данном этапе, используя
исходные данные, а и b, разобьем, построенный в области интегрирования
график функции f(x), на n = 10 отрезков. В дальнейшем каждый из них будет
достроен до прямоугольника, вычислено f(xi), а также площадь (Si) каждого из
них по формуле Si = f(xi) × h.
Исследование результатов функционирования разработанных программ
будет заключаться в том, на какое количество прямоугольников надо
разделить рассматриваемую область интегрирования, чтобы результат
соответствовал требуемой точности.
11
Таким образом, графический метод позволяет получать решения с
недостаточной точностью, но этот результат можно использовать для
контроля правильности работы программного проекта.
Графически численное интегрирование функции f(x) методом правых
прямоугольников представлено на рисунке 10.
f(x)
f = x - Cos(x)
h
Рисунок 5 – Интегрирование функции 𝑓(𝑥 ) на отрезке [0.5…2.5]
На рисунке показан график функции 𝒇(𝒙) на отрезке [0.5…2.5],
разделенном на n - 1 промежутков (10 - 1 = 9 частей).
Перейдем
к
вычислению
шага
дискретизации
h,
который при
интегрировании будет основанием прямоугольников, площадь которых
вычисляется по формуле:
Si = h × f(xi)
где ℎ:
𝑏−𝑎
𝑛−1
Таким образом, согласно заданному варианту шаг дискретизации h
ℎ=
будет равен:
ℎ=
2.5−0.5
10−1
= 0.222222
Далее были вычислены значения f(xi) и площадь Si любого из 9
прямоугольников вычислена, как произведение, найденного ранее f(xi) на шаг
дискретизации h. Общая сумма прямоугольников S на заданном отрезке
[0.5…2.5], соответствующая вычисляемому интегралу будет определена, как
12
сумма 9 площадей прямоугольников и равна 4.04536. Итог проделанных расчетов
представлены в таблице 2.
Таблица 2 – Результаты расчетов
x
f(x)
Si
0,5
0,72222
0,94444
1,16666
1,38888
1,61111
1,83333
2,05555
2,27777
2,5
0
0,34946
0,73583
1,15103
1,58556
2,02899
2,47044
2,89913
3,30490
3,67872
18,2041
0
0,07765
0,16351
0,25578
0,35234
0,45088
0,54898
0,64425
0,73442
0,81749
4,04535
Вывод,
вычислении
в
результате
исследования
положительного
применением
метода
значения
правых
графическим
численного
прямоугольников
4,04535
методом
при
интегрирования
получается
итог
с
с
переизбытком площади, а при отрицательном с недостатком. Другими
словами, выполненное подобным образом нахождение значения функции на
заданном отрезке позволяет использовать, полученные результаты при альфатестировании
путем
примененияв
качестве
разработки
программ,
реализующих численные методы разрешения данной проблемы.
Следующим шагом будет переход к разработке, отладке и тестированию
программы, реализующей численный метод интегирования рассматриваемой
фукнции на заданном отрезке с определенным количеством значений и
погрешностью.
Имена параметров в программах
Метод правых прямоугольников
A - нижний предел интегрирования
B - верхний предел интегрирования
S - значение интеграла
S1 - значение интеграла
H - шаг интегрирования
X - точки, в которых ищутся значения интегралов
N - количество интервалов
13
3 Разработка приложения для численного интегрирования
методом правых прямоугольников на языке Visual Basic for
Applications
Разработать
проект,
занимающийся
исследованием
численного
интегрирования функции f(x) на заданном отрезке [а, b] методом правых
прямоугольников. Площадь заданной области интегрирования найти с
заданной
погрешностью
h,
не
превосходящей
106.
В
качестве
пользовательского интерфейса программы использовать форму (Form),
причем погрешность h, должна и количество отрезков n относиятся к
исходным данным программы.
Отладку, тестирование и исполняемый файл (.exe) реализовать в среде
программирования Microsoft Visual Basic for Applicationsи и Visual Studio на
языке программирования Visual Basic for Applications. Результат представлен
на рисунке 2.
Рисунок 6 –Листинг программы на VBA
14
Исходные данные вводятся в созданное приложение и проверяются
путем тестирования. Щелчок по кнопке «Контроль F(a)» позволяет убедиться,
что f(a)= -0,3775826 (соответствует исходным данным) – значит функция f(х)
набрана правильно (рисунок 3).
Рисунок 7 –Ввод исходных данных и тестирование проекта
S=3.2278615 в функции "f = x - Cos(x) + 0.3775826 " Функция графически
разрешена, мы получили результаты.
Затем функция была написана на компьютере, чтобы получить решение
автоматически и была проблема.
После поиска проблемы мы нашли причину, То есть в графическом решении
мы приняли на 10 пунктов, Когда компьютер разрешает, это всего пунктов 9.
Следовательно, нет совпадения между результатами компьютера и
математическим решением. Таким образом, мы должны были изменить
формулу...
с
For x = a + h To b Step h
s = s + f(x)
Next x
к
For i = 1 To n - 1
x=a+i*h
s = s + f(x)
Next i
15
Функция поддерживается на более пунктов. Мы получили идентичные
результаты с индексом "i"
Рисунок 8 - Листинг программы на VBA, с индексом "i".
3.1 Описание методов программирования,
примененных в работе
Среда разработки и организация решения,
Курсовая
работа
выполнена
в
программирования MS Visual Studio 2012 и VBA.
16
интегрированной
среде
3.2 Листинги программы
Листинг файла «VBA»
Dim a As Single
Private Sub Btn_Exit_Click()
End
End Sub
Private Sub Btn_Fav_Click()
a = Txt_a
Txt_Fav = Round(f(a), 7)
End Sub
Private Sub Btn_Reset_Click()
Txt_h = ""
Txt_s = ""
End Sub
Private Sub Btn_S_Click()
n = Txt_n
a = Txt_a
b = Txt_b
h = (b - a) / (n - 1)
Txt_h = h
s=0
For x = a + h To b Step h
s = s + f(x)
Next x
Txt_s = Round(s * h, 7)
End Sub
17
Листинг файла «VB»
Public Class Form1
Dim a As Single
Function f(x)
f = x - Math.Cos(x) + 0.3775826
End Function
Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Btn_Fav.Click
a = Txt_a.Text
Txt_FaV.Text = Math.Round(f(a), 7)
End Sub
Private Sub Btn_S_Click(sender As Object, e As EventArgs) Handles Btn_S.Click
Dim h As Single
Dim x As Single
Dim n As Integer
Dim b As Single
Dim s As Single
n = Txt_n.Text
a = Txt_a.Text
b = Txt_b.Text
h = (b - a) / (n - 1)
Txt_h.Text = h
s=0
For i = 1 To n - 1
x=a+i*h
s = s + f(x)
Next i
Txt_S.Text = Math.Round(s * h, 6)
End Sub
Private Sub Btn_Reset_Click(sender As Object, e As EventArgs) Handles Btn_Reset.Click
Txt_h.Text = ""
Txt_S.Text = ""
End Sub
Private Sub Btn_Exit_Click(sender As Object, e As EventArgs) Handles Btn_Exit.Click
End
End Sub
Private Sub Txt_FaV_TextChanged(sender As Object, e As EventArgs) Handles
Txt_FaV.TextChanged
End Sub
End Class
18
3.3 Описание программы
При запуске программы на экран выводится главное окно программы с
отображенными и доступными элементами управления (см. рисунок 14).
Текстовые поля исходных данных заполнены значениями по умолчанию,
которые можно изменить.
Рисунок 9 – Главное окно программы после запуска
После нажатия кнопки «Вычислить площадь» организуется поток
выполнения вычислений. Во время расчетов программа продолжает
реагировать на действия пользователя, возможно сделать сброс для ввода
данных через кнопку «Сброс», а также закрыть программу нажав кнопку
«Выход» (рисунок 14).
19
Рисунок 10 – Главное окно программы в процессе
Далее делаем щелчок по кнопке «Вычислить площадь» и получаем
интегрирование
функции
f(x)
на
отрезке
[a;b]
методом
правых
прямоугольников с заданным числом отрезков 10, 100, 1000, 10000, 100000 и
1000000, представленных на рисунках 5-10. Он сходится со значением
функции f(x) и S при альфа-тестировании.
VBA
VS
Рисунок 11 – Получение интеграла функции f(x) на отрезке [a; b] при n=10
20
VBA
VB
Рисунок 12– Получение интеграла функции f(x) на отрезке [a; b] при n=100
VB
VBA
Рисунок 13 – Получение интеграла функции f(x) на отрезке [a; b] при n=1000
VBA
VB
Рисунок 14– Получение интеграла функции f(x) на отрезке [a; b] при n=10000
21
VBA
VB
Рисунок 15– Получение интеграла функции f(x) на отрезке [a; b] при n=100000
VB
VBA
Рисунок 16 – Получение интеграла функции f(x) на отрезке [a; b] при n=1000000
Из анализа информации, представленной на рисунке 3 можно сделать
следующие выводы о том, что Данные значения приблизительно равны, а
небольшие различия связаны с различным способом округления чисел при
промежуточных и конечных расчетах. Поэтому можно сказать, что значение
функции F(x) и ее интегрирование на заданном отрезке соответствует исходным
данным.
Таким образом, решение задачи различными способами, в данном случае
задействованы графический и численный методы доказывает правильность
функционирования разработанного программного продукта.
22
Заключение
Таким образом, при вычислении определенных интегралов методами
правых и правых прямоугольников решение не дает нам точного значения
интеграла, а только приближенное.
Чем ниже задается численное значение точности вычислений, тем
точнее результат, получаемый машиной. Для большей точности необходимо
большее число итераций.
Использование для вычисления метода (правых прямоугольников)
позволило исследовать зависимость точности вычислений при применении
метода.
Программы написаны на языке VB для вычисления значений
интегралов. Полученные в результате работы программ решения совпадают с
ответами в примере.
Этот метода требует больших вычислительных затрат, что связано с
довольно громоздкими формулами а также с большим объемом вычислений и
поэтому для относительно простых систем целесообразно использовать более
простые методы решения.
23
Список используемых источников
1.
Фокс Дж. Программное обеспечение и его разработка. М.:Мир,
2015. - 368 с.
2.
Лисков Б., Гатэг Дж. Использование абстракций и спецификаций
при разработке программ: Пер. с англ. - М.: Мир, 2014. - 424 с.
3.
Jackson M.-A. A Program Design. Academic Press, 2013.
4.
Goldberg A., Robson D.. Smalltalk-80: The Language and its
Implementation. Addison-Wesley, 2013.
5.
Meyer. D. Genericity. versus. Inheritance.. In. OOPSLA'86, SIGPLAN
Notices, v.21, n.11, 2016, pp. 391-405.
6.
Stroustrup D. The C++ Programming Language. Addison-Wesley,
7.
Borlang Turbo-Pascal v.6.0. Borland Inc, 2015.
8.
Иванов А.Г., Карпова А.В., Семик В.П., Филинов Ю.Е. Объектно-
2014.
ориентированная среда программирования. Системы и средства информатики.
Вып.2. М.: Наука, 2014.
24