Задание 1 тип B14
реклама
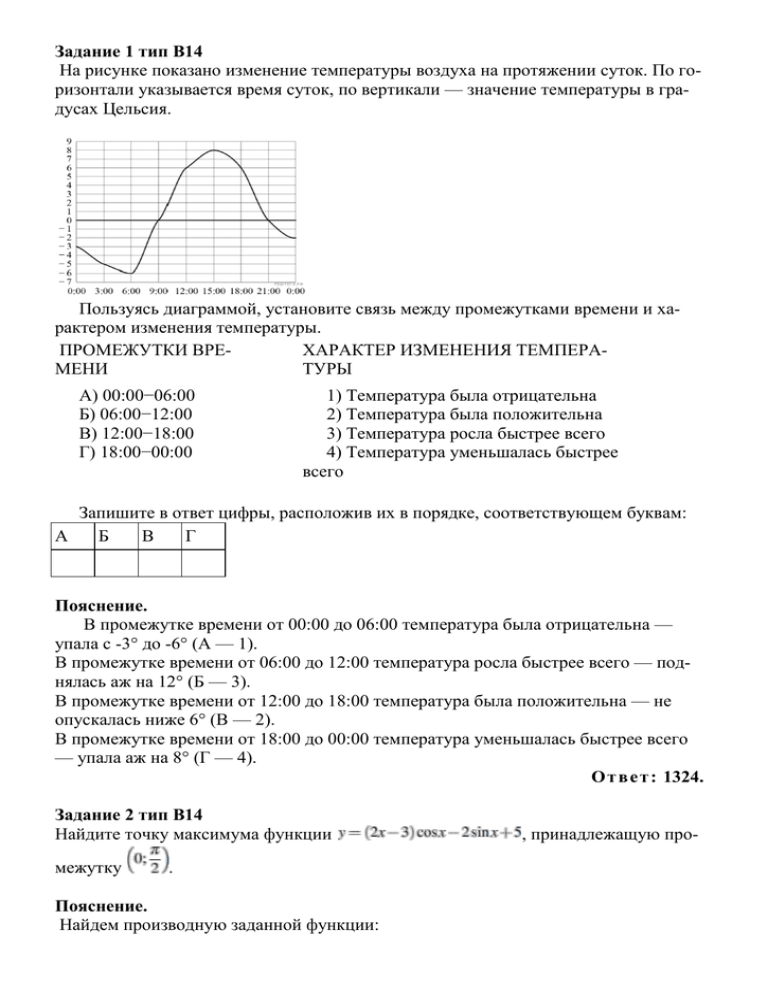
Задание 1 тип B14 На рисунке показано изменение температуры воздуха на протяжении суток. По горизонтали указывается время суток, по вертикали — значение температуры в градусах Цельсия. Пользуясь диаграммой, установите связь между промежутками времени и характером изменения температуры. ПРОМЕЖУТКИ ВРЕХАРАКТЕР ИЗМЕНЕНИЯ ТЕМПЕРАМЕНИ ТУРЫ А) 00:00−06:00 Б) 06:00−12:00 В) 12:00−18:00 Г) 18:00−00:00 1) Температура была отрицательна 2) Температура была положительна 3) Температура росла быстрее всего 4) Температура уменьшалась быстрее всего Запишите в ответ цифры, расположив их в порядке, соответствующем буквам: А Б В Г Пояснение. В промежутке времени от 00:00 до 06:00 температура была отрицательна — упала с -3° до -6° (А — 1). В промежутке времени от 06:00 до 12:00 температура росла быстрее всего — поднялась аж на 12° (Б — 3). В промежутке времени от 12:00 до 18:00 температура была положительна — не опускалась ниже 6° (В — 2). В промежутке времени от 18:00 до 00:00 температура уменьшалась быстрее всего — упала аж на 8° (Г — 4). О т ве т : 1324. Задание 2 тип B14 Найдите точку максимума функции межутку . Пояснение. Найдем производную заданной функции: , принадлежащую про- . На заданном промежутке (первая четверть без граничных точек) синус не обращается в нуль и принимает только положительные значения. Поэтому единственный нуль производной — число 1,5. Определим знаки производной функции: она положительна при x < 1,5 и отрицательна при x > 1,5. Поэтому искомая точка максимума — число 1,5. О т ве т : 1,5. Задание 3 тип B14 Найдите наибольшее значение функции на отрезке . Пояснение. Найдем производную заданной функции: Найдем нули производной: Определим знаки производной функции и изобразим на рисунке поведение функции: В точке заданная функция имеет максимум, являющийся ее наибольшим значением на заданном отрезке. Найдем это наибольшее значение: . О т ве т : 36. Задание 4 тип B14 Найдите точку минимума функции . Пояснение. Найдем производную заданной функции: . Найдем нули производной: Определим знаки производной функции и изобразим на рисунке поведение функции: Искомая точка минимума . О т ве т : 10. Задание 5 тип B14 Найдите наименьшее значение функции на отрезке . Пояснение. Найдем производную заданной функции: . Найдем нули производной: Определим знаки производной функции и изобразим на рисунке поведение функции: Сравним значения функции в точках 2 и 4: Тем самым, наименьшее значение функции на заданном отрезке равно 10. О т ве т : 10. Задание 6 тип B14 Найдите точку максимума функции межутку , принадлежащую про- . Пояснение. Найдем производную заданной функции: . На заданном промежутке (первая четверть без граничных точек) синус не обращается в нуль и принимает только положительные значения. Поэтому единственный нуль производной — число 1,5. Определим знаки производной функции: она положительна при x < 1,5 и отрицательна при x > 1,5. Поэтому искомая точка максимума — число 1,5 . О т ве т : 1,5. Задание 7 тип B14 Найдите наибольшее значение функции на отрезке Пояснение. Заметим, что и найдем производную этой функции: Найдем нули производной: Определим знаки производной функции и изобразим на рисунке поведение функции: Найденная производная неотрицательна на заданном отрезке, заданная функция возрастает на нем, поэтому наибольшим значением функции на отрезке является: О т ве т : 10.



