? S
реклама
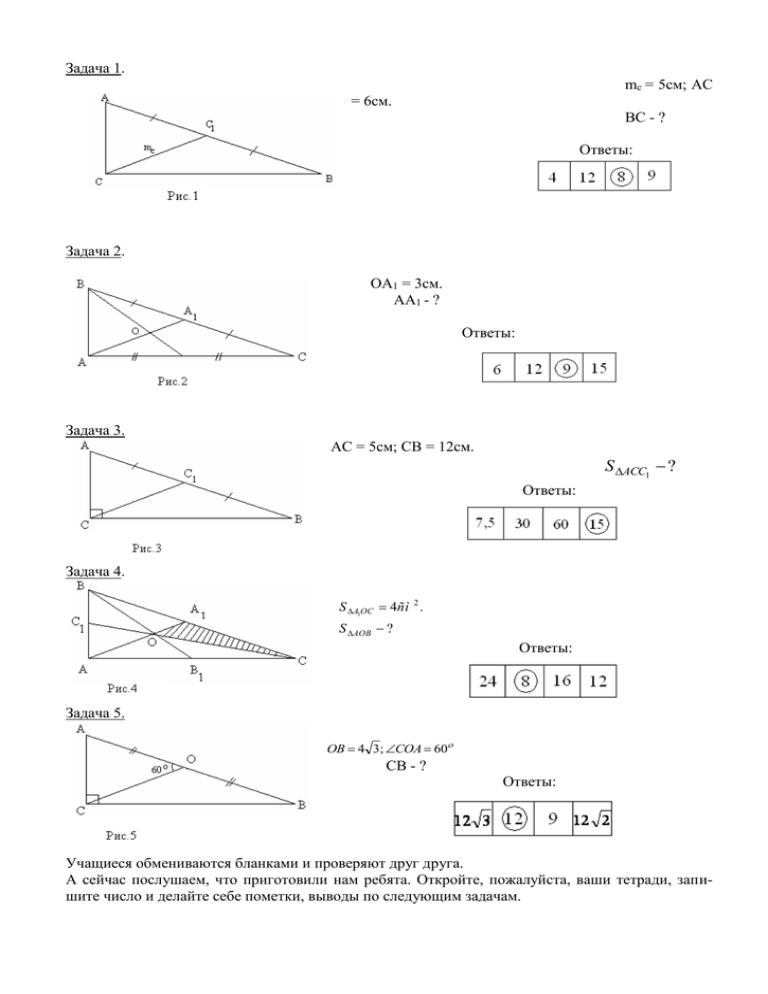
Задача 1. mс = 5см; AC = 6см. BC - ? Ответы: Задача 2. ОА1 = 3см. АА1 - ? Ответы: Задача 3. AC = 5см; CB = 12см. S ACC1 ? Ответы: Задача 4. S A1OC 4ñì 2 . S AOB ? Ответы: Задача 5. OB 4 3; COA 60 CB - ? Ответы: Учащиеся обмениваются бланками и проверяют друг друга. А сейчас послушаем, что приготовили нам ребята. Откройте, пожалуйста, ваши тетради, запишите число и делайте себе пометки, выводы по следующим задачам. Задача 1. Стороны треугольника АВС равны a, b, c. Вычислить длины медиан. Решение. 1) Проведем в ÀÂÑ одну медиану СС1 и продолжим ее за С1 на ее же длину, т.е. СС1 = С1Д. Получим параллелограмм по признаку АС = ДВ = b; ВС = АД = а. 2) По свойству параллелограмма (сумма квадратов диагоналей равна сумме квадратов его сторон) имеем: 2a 2 2b 2 c 2 CD 2 ; CD 2 2a 2 2b 2 c 2 ; (2CC1 ) 2 2a 2 2b 2 c 2 ; 2a 2 2b 2 c 2 1 ; mc 2a 2 2b 2 c 2 4 2 3) Аналогично можно вывести и для остальных медиан, т.е. имеем : 1 1 ma 2b 2 2c 2 a 2 ; mb 2a 2 2c 2 b 2 2 2 4mc2 2a 2 2b 2 c 2 ; mc2 Задача 2. Найти отношение площади ÀÂÑ к площади другого треугольника, стороны которого равны медианам ÀÂÑ . Решение. 1) Пусть S ABC S , а площадь треугольника, составленная из медиан S m . 2) На продолжении медианы ВВ1 отложим В1Д = ОВ1. 3) ÀOÂ1 CDB1 (по двум сторонам и углу между ними), значит АО = СД. 2 2 2 4) По свойству медиан в COD имеем: CO mc ; CD AO ma ; OD mb . 3 3 3 5) Таким образом, каждая сторона COD составляет две третьи сторон треугольника, со2 ставленного из медиан. Т.е. коэффициент подобия равен , а известно, что отношение 3 площадей подобных треугольников равно квадрату коэффициента подобия, т.е. 6) Но SCOD 2 SCOD 2 SCOD 4 9 ; ; S m SCOD . Sm Sm 9 4 3 S 4 1 9 1 3 S AOC S , тогда S m S ; S m S . Т.е. . 3 4 3 4 Sm 3 SCOD k 2; Sm Из рассуждений этой задачи следует вывод: три отрезка могут быть медианами некоторого треугольника тогда и только тогда, когда из них можно составить треугольник. Задача 3. В ÀÂÑ АС = 26 см, АА1и СС1 медианы . Найдите длину медианы ВВ1, если АА1= 36 см, СС1 = 15 см. Решение. 1) Пусть СС1 пересекается с АА1 в точке О. 2) Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины, тогда 2 2 AO AA1 ; AO 36; AO 24. 3 3 2 2 CO CC1 ; CO 15; CO 10 3 3 1 3) Тогда и OB1 BB1 ; BB1 3 OB1 3 4) Рассмотрим ÀOÑ : АО = 24; ОС = 10; АС = 26. Заметим, что 26 2 242 10 2 (верно), значит по обратной теореме Пифагора ÀOÑ прямоугольный; угол АОС равен 900, следовательно АС – гипотенуза, поэтому в нем ОВ1 – медиана; 1 1 OB1 AC; OB1 26; OB1 13. 2 2 5) Тогда ВВ1= 39. Ответ: 39 см. Итак, давайте подведем итог теоретической части нашего урока, и еще раз проговорим важные формулировки, а также вспомним о связи медиан с периметром треугольника (учащиеся еще раз проговаривают важные свойства медианы). Дальше, переходим к практической части урока. Задача 4. В треугольнике одна из сторон равна 26 дм, а ее медиана равна 16 дм. Определить две другие стороны этого треугольника, если они относятся как 3 : 5. Решение. 1 2a 2 2c 2 b 2 1) mb 2 (2 16) 2 2 9 x 2 2 25 x 2 26 2 32 2 18 x 2 50 x 2 676 68 x 2 1700 x 2 25; x 5 2) АВ = 15; ВС = 25. Ответ: 15; 25 Задача 5. Одна из сторон треугольника равна 10, а медианы двух других сторон равны 9 и 12. Найти площадь треугольника. Решение. 1) Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины. Значит 2 CO CC1 ; CO 8; AO 6; OA1 3 . 3 2) 1 S AOC S ABC ; S AOC 12 (12 10)(12 8)(12 6) ; . 3 S AOC 24 (можно лучше, если заметить, что треугольник АОС со сторонами 6, 8 и 10 является прямоугольным, тогда площадь можно найти как половину произведения катетов). 3) S ABC 3 24 72 Ответ: 72 кв.ед. Задача 6. Медианы треугольника равны 9, 12 и 15. Найти площадь треугольника. Решение. 1) Найдем площадь треугольника, составленного из медиан. Sm 18(18 9)(18 12)(18 15) ; Sm 54. 3 4 4 2) S m S ; S S m ; S 54 72 . 4 3 3 Ответ: 72 кв.ед. Задача 7. Площадь ABC равна 60 см2; медиана ВВ1 =15 см, COB1 300 . Найти СО; СС1. Решение. 1 1 S ABC ; S COB1 60 10 . 6 6 1 1 1 S COB1 CO OB1 sin 30 ; S COB1 CO 5 ; 2 2 2 4 4 S COB1 5CO; CO 10 8 5 1) SCOB1 2 3 3) CO CC1 ; CC1 CO; CC1 12. 3 2 Ответ: 8 см, 12 см. Задача 8. Точка пересечения медиан прямоугольного треугольника удалена от его катетов на расстояние 3 см и 4 см. Найдите расстояние от этой точки до гипотенузы. Решение. 1) КСМО – прямоугольник, значит СМ = 4, КС = 3. 2) CMO – прямоугольный: СО = 5; 3 3 15 ÑÑ1 CO; ÑÑ1 5 . По свойству медианы 2 2 2 АВ =15. 3) Пусть АС = х; СВ = у. 1 3 3 S AOC x 4; S AOC 2 x 2 x y; x y . 2 2 4 1 3 SCOB y 3; SCOB y 2 2 9 2 ACB : x 2 y 2 225; y y 2 22; y 12. 4) 16 x9 S AOB 2 x; S AOB 18. 5) 2S 1 36 S AOB AB OP; OP AOB ; OP ; OP 2,4 2 AB 15 S AOC SCOB S AOB Ответ: 2,4 см Задача 9. В прямоугольном треугольнике АВС (угол С 900) медианы СС1 и ВВ1 перпендикулярны друг другу. Найти длины этих медиан, если длина третьей медианы АА1 = 3 3 . Решение. 1) Пусть ОС1 = х; ОВ1= у, тогда СО = 2х; ВО = 2у. 1 1 2) Известно, что АА1 = 3 3 ; но OA1 AA1 ; OA1 3 3 3. 3 3 3) COB - прямоугольный, ОА1 – медиана, проведенная из вершины прямого угла, значит ОА1 = ½ СВ; СВ = 2 ОА1; СВ = 2 3 . 4) Тогда в COB прямоугольном 4х2 + 4у2 = ( 2 3 )2; х2 + у2 = 3 (1) 5) B1CB - прямоугольный: B1C 2 (3 y ) 2 (2 3 ) 2 ; B1C 2 9 y 2 12 . 6) B1OC - прямоугольный: B1C 2 y 2 4 x 2 . 7) Тогда 9 y 2 12 = y 2 4x 2 ; 2у2 = х2 + 3 (2). 8) Из равенства (1) выразим х2 =3 - у2 и подставим в равенство (2). 2 y 2 3 y 2 3; 3 y 2 6; y 2 2; y 2 , тогда х = 1. 9) Значит ВВ1 = 3у ; ВВ1 = 3 2 ; СС1= 3 х; СС1 = 3. Ответ: 3 2 ; 3. С последней задачей работает учитель вместе с учениками. Задача 10. Существуют ли такие четыре точки пространства А, В, С и Д, что AB CD 8; AC BD 10; AD BC 13 ? Решение. Раз речь у нас идет о пространстве, то данные точки будем считать вершинами тетраэдра. Вот и нарисуем тетраэдр, у которого все ребра отвечают условию задачи. А теперь остановимся и порассуждаем. Естественно, найдем аналогию с планиметрией. Фигура на плоскости, аналогичная тетраэдру - треугольник. И вы помните, что стороны треугольника не могут быть любыми отрезками – любая сторона треугольника должна быть меньше суммы двух других. Так же обстоят дела и с тетраэдром. Откуда мы знаем, что существует тетраэдр с любыми ребрами? Ясно, что с любыми не существует. Ведь каждая грань – треугольник, а значит, для его ребер, лежащих в каждой грани, должно выполняться неравенство треугольника. Давайте проверим, выполняется ли неравенство треугольника для ребер каждой грани? (да). Но может быть, есть и другие условия, необходимые для существования тетраэдра с шестью произвольными ребрами? Поскольку, сегодня речь идет о медианах, естественно хочется использовать их. Итак, проведем в гранях АВС и ДВС медианы к стороне СВ. Таким образом, мы получим треугольник АДК из двух медиан и ребра АД. Проверим, существует ли он? 1 1 AK 2 82 2 10 2 169 ; AK 159 . Найдем длину АК. Заметим, что 2 2 1 1 1 ABC CDB; AK DK 159 . Тогда 159 159 13 , т.е. 159 169 , что неверно. 2 2 2 Таким образом, такой тетраэдр не существует, то есть, таких точек нет. Ответ: нет.

