Задача 27
реклама

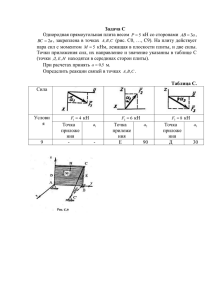
Задача 27 Вариант 2821 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 1, F2/P= 2, β= 0,5, Δ= ΔA. Задача 27 Вариант 2822 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 1, F2/P= 3, β= 0,6, Δ= ΔBB. Задача 27 Вариант 2823 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 1, F2/P= -2, β= 0,8, Δ= ΔAA. Задача 27 Вариант 2824 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 1, F2/P= 4, β= 0,4, Δ= ΔA. Задача 27 Вариант 2825 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 1, F2/P= 4, β= 0,5, Δ= ΔA. Задача 27 Вариант 2826 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= -1, F2/P= 3, β= 0,8, Δ= ΔB. Задача 27 Вариант 2828 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 2, F2/P= 1, β= 0,5, Δ= ΔBB. Задача 27 Вариант 2829 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1,5, b/ l= 0,5, S2/ S= 1,5, F1/P= 1, F2/P= 5, β= 0,8, Δ= ΔB. Задача 27 Вариант 8210 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1, b/ l= 1, S2/ S= 2,2, F1/P= -1, F2/P= 3, β= 0,8, Δ= ΔB. Задача 27 Вариант 8211 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1, b/ l= 1, S2/ S= 2,2, F1/P= 1, F2/P= 2, β= 0,5, Δ= ΔA. Задача 27 Вариант 8212 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1, b/ l= 1, S2/ S= 2,2, F1/P= 1, F2/P= 3, β= 0,6, Δ= ΔBB. Задача 27 Вариант 8213 Условие задачи. Для заданной (см. рис.) статически неопределимой фермы требуется: 1) из расчёта на прочность по наибольшим напряжениям вычислить допустимое значение параметра нагрузки Р; 2) найти температурные напряжения в элементах схемы, если температура стержней с площадью S1 изменяется на ΔТ; 3) определить монтажные напряжения в элементах системы, если длина стержней площадью S2 отличается на величину δ от проектной длины; 4) исследовать поведение фермы при возрастающей нагрузке. Для этого определить (в долях σTS) характерные нагрузки РТ и Ро, соответствующие началу возникновения в системе пластических деформаций и состоянию предельного равновесия и построить в относительных величинах Р/σTS, σi/σT и Δ/(σT/E) (σi – напряжение в i-ом стержне, Δ – перемещение заданной точки) графики зависимостей напряжений и указанного перемещения от возрастающей нагрузки; 5) вычислить коэффициент запаса прочности по предельному равновесию; 6) определить остаточные напряжения в ферме и остаточное напряжение указанной точки после нагружения системы до значения Р= РТ+β(Ро–РТ) и последующей нагрузки. Принять l=40 см, S=4 см(2), материал стержней – идеально упруго-пластический, σT= 240 МПа, α= 12*10(-6) I/°C, [nT]= 2,0. S1/ S= 1,5, ΔТ= -50 град, δ= 1 мм, a/ l= 1, b/ l= 1, S2/ S= 2,2, F1/P= 1, F2/P= -2, β= 0,8, Δ= ΔAA.