task_13044x

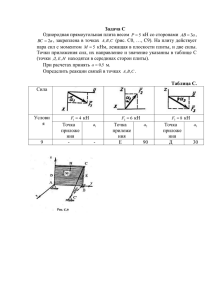
Задача К1
Точка В движется в плоскости XY (рис. К1.0…К1.9; траектория точки на рисунке
показана условно). Закон движения точки задан уравнениями X  f1 (t ) , Y  f 2 (t ) , где
X и Y выражены в сантиметрах, t - в секундах. Зависимость X  f1 (t ) указана
непосредственно на рисунках, зависимость Y  f 2 (t ) дана в табл. К1.
Найти уравнение траектории точки, определить скорость и ускорение точки, а
также ее касательное и нормальное ускорение и радиус кривизны для момента
времени t  1 с.
В некоторых вариантах задачи в процессе решения следует выполнить
необходимые тригонометрические преобразования, а также учесть известные
тригонометрические тождества.
y
В
·
·

xB  4 cos( t )
6
x
Рис. К1.1
Номер
условия
8
P.S. Рис. К1.1
Y  f 2 (t )
Рис. 0-2
 
6 cos t   4
3 
Задача К2
Плоский механизм состоит из стержней, соединенных между собой и с
неподвижными опорами цилиндрическими шарнирами. Схемы механизмов
приведены на рисунках К2.0, …, К2.9. Положение механизма определяется углами  ,
 ,  ,  ,  , значения которых даны в табл. К2.а и К2.б. Длины стержней: l1  0,4 м,
l2  1,2 м, l3  1,4 м, l4  0,6 м. Точка Д находится посередине стержня «2».
Заданы угловая скорость и угловое ускорение одного из стержней механизма или
скорость и ускорение точек этих стержней. Определить кинематические
характеристики точек и стержней, указанные в столбце «найти».
Положительным направлением угловых скоростей и ускорений считать против хода
часовой стрелки, линейных скоростей и ускорений – от точки « В » к точке « в ».
№
у
с
л.

8
60
Углы, град.

15
0

12
0
Дано

90

30
Найти
1
4
1/с
1/с
2
-
V
т
о
ч.
Д,
Е

a

зве
н
а
то
ч
.
зве
на
АВ
В
АВ
Задача Д 1
Тело массой m движется поступательно по траектории ABC , расположенной в
вертикальной плоскости. Участки траектории AB и BC прямолинейны.
В точке A тело имеет начальную скорость V0 . Кроме того задана длина участка AB(l1 )
или время движения тела по этому участку t1 .
На указанных участках на тело действуют различные системы сил: кроме силы тяжести
и реакции опоры на участке АВ действует постоянная сила Q и зависящая от скорости
тела сила сопротивления R , на участке BC - сила трения скольжения F тр и
переменная во времени F . Коэффициент трения скольжения f  0,1 .
Требуется определить закон движения тела на участке BC : x  f (t ) .
Величины m , Q , R , F  f (t ) , V0 , l1 , t1 заданы в табл.Д1.
При решении следует учитывать, что конечная скорость движения тела на участке
AB(VB ) является начальной скоростью для участка BC
№
усло
в.
8
m , кг
V0 , м/с
Q, Н
R,Н
l, м
t1 , с
4,8
10
10
0,2 V 2
4
-
D
B
•
•
Рис.Д1.0
P.S. Рис. Д1.1
А
•
Q
Рис.Д1.1
F
,Н
4 cos( 2t )
D
•
x
300
Задача Д2
Механическая система состоит из груза 1 массой m1 , ступенчатого шкива 2 массой m2 с
радиусом R2 , r2 и радиусом инерции 2 , шкива 3 с радиусом R3 и распределенной по
ободу массой m3 , и сплошного катка 4 массой m4 . Тела соединены нитью. К одному из
тел присоединена пружина с жесткостью С . При движении на шкив 2 действует момент
сопротивления М С , на тело 1 – сила трения F ТР . Коэффициент трения f  0,1 .
Система из состояния покоя приходит в движения под действием силы F  f (t ) ,
приложенной к грузу 1.
Значение входящих в условие задачи величин приведены в табл. Д2, схемы
механизмов – на рис. Д2.0, …, Д2.9.
№
усло
в.
8
m1 , кг
m2 , кг
m3 , кг
m4 , кг
C,
Н/м
4
2
2
6
320
MC
,
Н
м
1,4
F  f (S ) ,
Найти
Н
50(9  2 S )
4
Задача Д3
Вертикальный вал AK (рис. Д3.0…Д3.9, табл. Д3), вращающийся с постоянной
угловой скоростью   10 с-1, закреплен подпятником в точке А и цилиндрическим
подшипником в точке, указанной в таблице Д3 в столбце 2 ( АВ  ВД  ДЕ  ЕК  l ). К валу
жестко прикреплен невесомый стержень – 1 длиной l1  0,4 м, с точечной массой m1  6
кг на конце и однородный стержень 2 длинной l2  0,6 м, имеющий массу m2  4 кг; оба
стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице
Д3 в столбцах 3 и 4, а углы  и  - в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При
окончательных подсчетах принять l  0,4 м.
№ условия
8
Подшипник Стержень 1 Стержень 2
D
E
K
Угол α
75
Угол β
60