Задачи для 11 класса

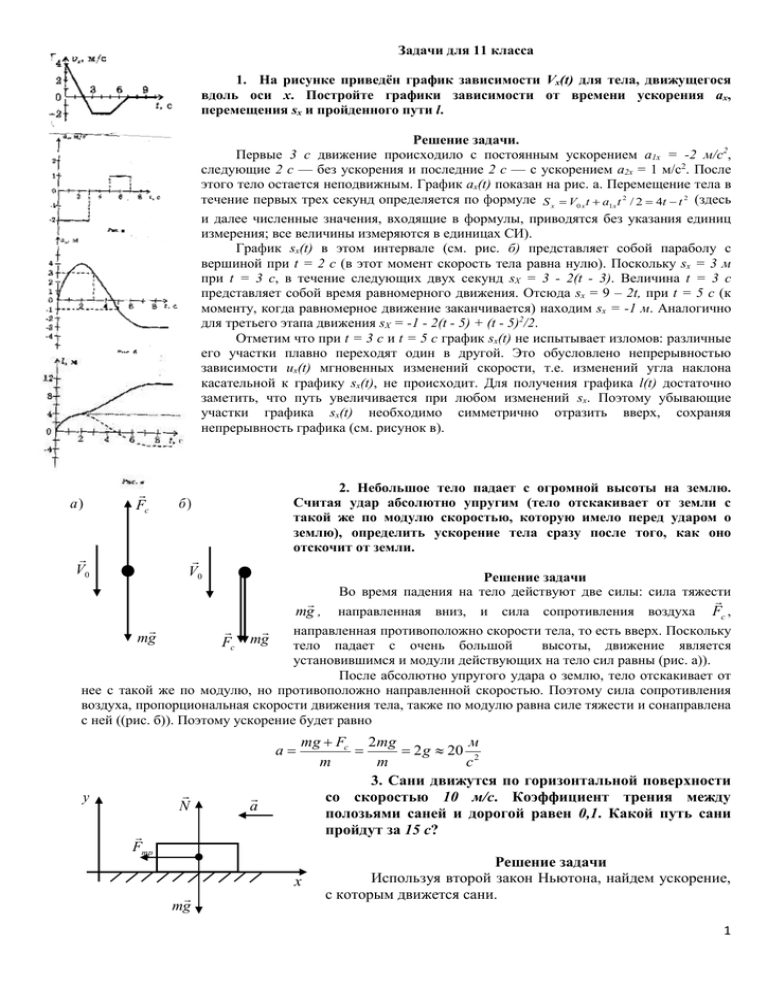
Задачи для 11 класса
1. На рисунке приведён график зависимости Vx(t) для тела, движущегося
вдоль оси x. Постройте графики зависимости от времени ускорения ax,
перемещения sx и пройденного пути l.
Решение задачи.
Первые 3 с движение происходило с постоянным ускорением а1х = -2 м/с2,
следующие 2 с — без ускорения и последние 2 с — с ускорением а2х = 1 м/с2. После
этого тело остается неподвижным. График ах(t) показан на рис. а. Перемещение тела в
течение первых трех секунд определяется по формуле S x  V0 x t  a1x t 2 / 2  4t  t 2 (здесь
и далее численные значения, входящие в формулы, приводятся без указания единиц
измерения; все величины измеряются в единицах СИ).
График sx(t) в этом интервале (см. рис. б) представляет собой параболу с
вершиной при t = 2 с (в этот момент скорость тела равна нулю). Поскольку sх = 3 м
при t = 3 с, в течение следующих двух секунд sХ = 3 - 2(t - 3). Величина t = 3 с
представляет собой время равномерного движения. Отсюда sх = 9 – 2t, при t = 5 с (к
моменту, когда равномерное движение заканчивается) находим sx = -1 м. Аналогично
для третьего этапа движения sХ = -1 - 2(t - 5) + (t - 5)2/2.
Отметим что при t = 3 с и t = 5 с график sx(t) не испытывает изломов: различные
его участки плавно переходят один в другой. Это обусловлено непрерывностью
зависимости ux(t) мгновенных изменений скорости, т.е. изменений угла наклона
касательной к графику sx(t), не происходит. Для получения графика l(t) достаточно
заметить, что путь увеличивается при любом изменений sx. Поэтому убывающие
участки графика sx(t) необходимо симметрично отразить вверх, сохраняя
непрерывность графика (см. рисунок в).
а)

Fc

V0
2. Небольшое тело падает с огромной высоты на землю.
Считая удар абсолютно упругим (тело отскакивает от земли с
такой же по модулю скоростью, которую имело перед ударом о
землю), определить ускорение тела сразу после того, как оно
отскочит от земли.
б)

V0

mg ,
Решение задачи
Во время падения на тело действуют две силы: сила тяжести

направленная вниз, и сила сопротивления воздуха Fc ,



направленная противоположно скорости тела, то есть вверх. Поскольку
mg
Fc mg
тело падает с очень большой
высоты, движение является
установившимся и модули действующих на тело сил равны (рис. а)).
После абсолютно упругого удара о землю, тело отскакивает от
нее с такой же по модулю, но противоположно направленной скоростью. Поэтому сила сопротивления
воздуха, пропорциональная скорости движения тела, также по модулю равна силе тяжести и сонаправлена
с ней ((рис. б)). Поэтому ускорение будет равно
a

N
y

Fтр

a
mg  Fc 2mg
м

 2 g  20 2
m
m
с
3. Сани движутся по горизонтальной поверхности
со скоростью 10 м/с. Коэффициент трения между
полозьями саней и дорогой равен 0,1. Какой путь сани
пройдут за 15 с?
x

mg
Решение задачи
Используя второй закон Ньютона, найдем ускорение,
с которым движется сани.
1

 

ma  Fтр  N  mg
ox : ma  Fтр
Fтр  N
oy : 0  N  mg
м
с2
Таким образом, можно сделать вывод, что сани остановились через   10 с , а остальное
время они покоились. Исходя из этого, найдем пройденный путь:
a 2
S  V0 
 50 м
2
a  g  1
4. Космический корабль, имеющий скорость V = 10 км/с, попадает в неподвижное облако
микрометеоров. В объеме V0 = 1 м3 пространства находится n = 1 микрометеоров. Масса каждого
микрометеора m0 = 2·10-5 кг. На сколько должна возрасти сила тяги двигателя, чтобы скорость
корабля при прохождении через облако не изменилась? Лобовое сечение корабля S = 49 м2. Удар
микрометеоров об обшивку корабля считать неупругим.
Решение задачи.
При движении космического корабля в облаке микрометеоров частицы
получают импульс со стороны обшивки, в результате чего их скорость
возрастет от 0 до скорости корабля V, поскольку удар неупругий.
Одновременно такой же импульс, как и частицы, получает и корабль, но в
сторону, противоположную движению. В результате скорость корабля должна
уменьшаться и для ее сохранения сила тяги двигателя должна возрасти.
Прирост силы тяги должен быть тем большим, чем больше изменение импульса
частиц за единицу времени.
Выделим (рис. 2.8) часть микрометеорного облака, которой был сообщен импульс за небольшой
промежуток времени t , в течение которого движение корабля можно считать равномерным.
Если за время дt корабль пройдет расстояние l, то импульс частиц, находящихся в объеме
цилиндра А, возрастет от 0 до mu, частицы станут двигаться вместе с кораблем. Такое изменение
количества движения произойдет за счёт импульса силы F t , действующего на выделенную часть
облака со стороны обшивки корабля. Сила F будет равна при этом по величине и направлению
искомому увеличению силы тяги.
Учитывая, что вначале частицы покоились и направления векторов F t и mu совпадают, по
второму закону Ньютона:
Ft  mV (1)
Масса частиц, увлекаемых за время дt равна:
m
nm0
Sl. (2)
V0
При малом t можно с достаточной степенью точности считать, что движение на участке l
равномерное и, следовательно,
l  Vt. (3)
Из уравнений (1)—(3) находим, что искомое увеличение силы тяги равно:
F
nm0 Sv 2
; F  100кн.
V0
5. В теплоизолированный сосуд с нагревателем внутри помещены
1 кг льда и 1 кг легкоплавкого вещества, не смешивающегося с водой.
Сначала температура в сосуде была равна - 40оС, затем включили
нагреватель, потребляющий постоянную мощность. Зависимость
температуры в сосуде от времени показана на рисунке. Удельная
теплоёмкость льда сл = 2·103 Дж / (кг·0С), твёрдого вещества –
с = 1·103 Дж / (кг·0С). Найти удельную теплоту плавления вещества и его
удельную теплоёмкость в расплавленном состоянии.
2
Решение задачи.
Из графика видно, что температура плавления
неизвестного вещества равна - 20°С. Для нагрева содержимого
сосуда от t1= - 40 °С до t2= - 20 °С потребовалось время T=1
мин = 60 с. При этом от нагревателя было получено
количество теплоты Q=PT1, где Р - мощность нагревателя.
Поскольку массы льда и неизвестного вещества одинаковы,
PT = m(c1 + c)(t2- t1) Для полного плавления вещества в
течение T2 = 5/ 3 мин = 100с потребовалось количество
теплоты, равное
Поделив это уравнение на предыдущее, найдем
удельную теплоту плавления неизвестного вещества:
  (с л  c)(t 2  t1 )( 2 /  1 )  10 5 Дж / кг
Для дальнейшего нагрева смеси льда и расплава вещества до температуры t3=0°С в течение T3
=4/3 мин = 80 с потребовалось количество теплоты, равное
P  m(c л  c)(t 2  t1 ).
где с - удельная теплоемкость вещества в расплавленном состоянии. Сравнивая первый и
последний этапы процесса, найдем
с` (c л  c)
t 2  t1 3
 2 *10 3 Дж /( кг *о С ).
t 2  t1 1
6. При подключении к аккумулятору с внутренним сопротивлением r = 0,16 Ом
нагревательный элемент развивает мощность N1=200 Вт. При подключении нагревательного
элемента к двум таким аккумуляторам, соединённым последовательно, выделяемая в нагревателе
мощность составила N2=288 Вт. Найдите ЭДС аккумулятора.
Решение задачи
Мощность, выделяемая и нагревательном элементе при подключении его к одному аккумулятору,
равна N1 
 2R
(r  R) 2
, где R - сопротивление нагревателя,  ЭДС аккумулятора, r - его внутреннее
сопротивление. При подключении нагревателя к двум одинаковым аккумуляторам, соединённым
последовательно, ЭДС и внутреннее сопротивление источника удваиваются, в результате чего мощность,
выделяющаяся в нагревателе, будет N 2 
4 2 R
. Вводя величину k 
(2r  R) 2
2r (k  1)
R
Отсюда
.
Учитывая,
2k
rN 2

 12 В
N2
N2
2(2 
)(
 1)
N1
N1
что
rR
N2
, получаем k  2
.
2r  R
N1
(r  R) 2
 
N1
R
2
получаем
ответ:
3