Задачи для 10 класса

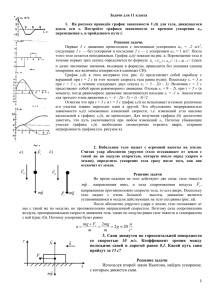
Задачи для 10 класса
1. Автомашина прошла половину пути со скоростью V0. На
оставшейся части пути она половину времени двигалась со скоростью
V1, а последний участок прошла со скоростью V2. Найти среднюю скорость за всё время движения автомашины.
Решение задачи
Средняя скорость Vср по определению равна отношению пройденного пути L ко всему времени движения t, т.е.
Vср 
L
(1)
t
Первую половину пути автомашина прошла за время t1 
L
.
2V0
Пусть t2 - время прохождения второй половины пути. На оставшейся части
пути она половину времени двигалась со скоростью V1 и прошла путь
t2
, а другую половину времени двигалась со скоростью V2 и про2
t
t
t
L
L
 L1  L2  V1 2  V2 2  t 2 
шла путь L2  V2 2 . Поэтому
.
2
2
2
2
V1  V2
L1  V1
После подстановки t1 и t2 в (1) находим
Vср 
2V0 (V1  V2 )
(2V1  V1  V2 )
2. Небольшое тело падает с огромной высоты на землю. Считая
удар абсолютно упругим (тело отскакива
ет от земли с такой же по модулю скороб)
а)
Fc
стью, которую имело перед ударом о землю), определить ускорение тела сразу после того, как оно отскочит от земли.


Решение задачи
V
V
0
0
Во время падения на тело действуют

две силы: сила тяжести mg , направленная

вниз, и сила сопротивления воздуха Fc ,

mg


Fc mg
направленная противоположно скорости тела, то есть вверх. Поскольку
тело падает с очень большой высоты, движение является установившимся
и модули действующих на тело сил равны (рис. а)).
После абсолютно упругого удара о землю, тело отскакивает от нее с
такой же по модулю, но противоположно направленной скоростью. Поэтому сила сопротивления воздуха, пропорциональная скорости движения тела, также по модулю равна силе тяжести и сонаправлена с ней ((рис. б)).
Поэтому ускорение будет равно
a
mg  Fc 2mg
м

 2 g  20 2
m
m
с
3. Космический корабль, имеющий скорость V = 10 км/с, попадает в неподвижное облако микрометеоров. В объеме V0 = 1 м3 пространства находится n = 1 микрометеоров. Масса каждого микрометеора m0 = 2·10-5 кг. На сколько должна возрасти сила тяги двигателя,
чтобы скорость корабля при прохождении через облако не изменилась? Лобовое сечение корабля S = 49 м2. Удар микрометеоров об обшивку корабля считать неупругим.
Решение задачи.
При движении космического корабля в облаке микрометеоров частицы получают импульс со стороны обшивки, в результате чего их скорость возрастет от 0 до
скорости корабля V, поскольку удар неупругий. Одновременно такой же импульс, как и частицы, получает и корабль, но в сторону, противоположную движению. В результате скорость корабля должна уменьшаться и для ее сохранения сила
тяги двигателя должна возрасти. Прирост силы тяги должен быть тем
большим, чем больше изменение импульса частиц за единицу времени.
Выделим (рис. 2.8) часть микрометеорного облака, которой был сообщен импульс за небольшой промежуток времени t , в течение которого
движение корабля можно считать равномерным.
Если за время дt корабль пройдет расстояние l, то импульс частиц,
находящихся в объеме цилиндра А, возрастет от 0 до mu, частицы станут
двигаться вместе с кораблем. Такое изменение количества движения произойдет за счёт импульса силы F t , действующего на выделенную часть
облака со стороны обшивки корабля. Сила F будет равна при этом по величине и направлению искомому увеличению силы тяги.
Учитывая, что вначале частицы покоились и направления векторов
F t и mu совпадают, по второму закону Ньютона:
Ft  mV (1)
Масса частиц, увлекаемых за время дt равна:
m
nm0
Sl. (2)
V0
При малом t можно с достаточной степенью точности считать, что
движение на участке l равномерное и, следовательно,
l  Vt. (3)
Из уравнений (1)—(3) находим, что искомое увеличение силы тяги
равно:
nm0 Sv 2
F
; F  100кн.
V0
4. В цилиндре под поршнем находятся воздух, водяной пар и вода. Число молей воздуха в n = 3 раза превышает число молей водяного
пара, а масса воды равна массе водяного пара. Объём смеси изотермически увеличивают до тех пор, пока вся вода не испарится. Определите отношение давлений в цилиндре в конечном и начальном состояниях.
Решение задачи
Считая, что воздух и насыщенный водяной пар подчиняются уравнению Менделеева-Клапейрона, запишем уравнения начального состояния
этих веществ:
pV0   в RT , pнV0   н RT ,
где р и рп - парциальные давления воздуха и насыщенного пара в
смеси, R -универсальная газовая постоянная, T и V0 - абсолютная температура и начальный объём смеси,  в - число молей воздуха,  н - число молей
водяного пара в начальном состоянии, причём, по условию,  в  n н . Отсюда:
p
n н RT
 RT
, pн  н
V0
V0
По закону Дальтона, начальное давление смеси воздуха и водяного
пара
в цилиндре p0  p  pн 
(n  1) н RT
.
V0
Поскольку масса воды в цилиндре равна начальной массе пара, то
для того чтобы вся пода испарилась, объём смеси нужно увеличить в 2 раза.
При этом давление воздуха в цилиндре станет равным
p
, а давление пара
2
не изменится. Следовательно, конечное давление смеси в цилиндре
(n  2) н RT
p
 pн 
2
2V0
pк
n2

 0,625
р0 2(n  1)
pк 
5. В теплоизолированный сосуд с
нагревателем внутри помещены 1 кг льда и
1 кг легкоплавкого вещества, не смешивающегося с водой. Сначала температура в
сосуде была равна - 40оС, затем включили
нагреватель, потребляющий постоянную
мощность. Зависимость температуры в сосуде от времени показана на рисунке.
Удельная
теплоёмкость
льда
сл = 2·103 Дж / (кг·0С), твёрдого вещества – с = 1·103 Дж / (кг·0С). Найти
удельную теплоту плавления вещества и его удельную теплоёмкость в
расплавленном состоянии.
Решение задачи.
Из графика видно, что температура плавления неизвестного вещества
равна - 20°С. Для нагрева содержимого сосуда от t1= - 40 °С до t2= - 20 °С
потребовалось время T=1 мин = 60 с. При этом от нагревателя было получено количество теплоты Q=PT1, где Р - мощность нагревателя. Поскольку массы льда и
неизвестного вещества одинаковы,
PT = m(c1 + c)(t2- t1) Для полного плавления вещества в течение T2 = 5/ 3 мин = 100с
потребовалось количество теплоты, равное
Поделив это уравнение на предыдущее,
найдем удельную теплоту плавления неизвестного вещества:
  (с л  c)(t 2  t1 )( 2 /  1 )  10 5 Дж / кг
Для дальнейшего нагрева смеси льда и расплава вещества до температуры t3=0°С в течение T3 =4/3 мин = 80 с потребовалось количество теплоты, равное
P  m(c л  c)(t 2  t1 ).
где с - удельная теплоемкость вещества в расплавленном состоянии.
Сравнивая первый и последний этапы процесса, найдем…..