б) площадь сечения куба плоскостью ACD.
реклама

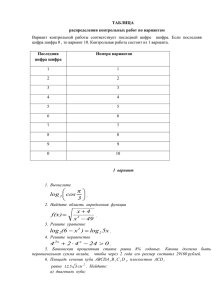
ТАБЛИЦА распределения контрольных работ по вариантам Вариант контрольной работы соответствует последней цифре шифра. Если последняя цифра шифра 0 , то вариант 10. Контрольная работа состоит из 1 варианта. Последняя цифра шифра Номера вариантов 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 0 10 1 вариант 1. Вычислите π log 2 cos . 3 2. Найдите область определения функции x4 f(x) . x 2 49 3. Решите уравнение log 2(6 x 2 ) log 2 5x . 4. Решите неравенство 4 2x 2 4 x 24 0 . 5. Банковская процентная ставка равна 8% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 29160 рублей. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ACD 1 равна 12,5 3 см 2 . Найдите: а) диагональ куба; б) площадь сечения куба плоскостью ABC 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =4, а АВ=ВС=2. Вычислите косинус угла между векторами ВА1 и ВС1 . 8. В вазе лежат яблоки: 10 зеленых и 5 красных. Сколькими способами можно взять из вазы 3 зеленых и 2 красных яблока? 2 вариант 1. Вычислите π log 3 tg . 3 2. Найдите область определения функции 6x x 2 f(x) log 5 . x2 3. Решите уравнение 3x 2 3x 10 2x . 4. Решите неравенство 2 2x 6 2 x 16 0 . 5. Банковская процентная ставка равна 12% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 18816 рублей. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ABC 1 равна 81 2 см 2 . Найдите: а) диагональ куба б) площадь сечения куба плоскостью ACD 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =6, а АВ=ВС=3. Вычислите косинус угла между векторами ВА1 и ВС1 . 8. В вазе лежат яблоки: 12 желтых и 6 красных. Сколькими способами можно взять из вазы 4 желтых и 2 красных яблока? 3 вариант 1. Вычислите π log 2 sin . 6 2. Найдите область определения функции f(x) 36 x 2 . x3 3. Решите уравнение log 4(12 x 2 ) log 4 x . 4. Решите неравенство 5 2x 2 5 x 35 0 . 5. Банковская процентная ставка равна 7% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 34347 рублей. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ACD 1 равна 18 3 см 2 . Найдите: а) диагональ куба; б) площадь сечения куба плоскостью ABC 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =4, а АВ=ВС=2. Вычислите косинус угла между векторами В1 А и В1С . 8. В вазе лежат яблоки: 10 зеленых и 5 красных. Сколькими способами можно взять из вазы 2 зеленых и 3 красных яблока? 4 вариант 1. Вычислите π log 3 ctg . 6 2. Найдите область определения функции x3 f(x) log 5 2 . x 7x 3. Решите уравнение 8x 2 2x 8 3x . 4. Решите неравенство 3 2x 7 3 x 18 0 . 5. Банковская процентная ставка равна 11% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 24642 рубля. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ABC 1 равна 64 2 см 2 . Найдите: а) диагональ куба б) площадь сечения куба плоскостью ACD 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =6, а АВ=ВС=3. Вычислите косинус угла между векторами В1 А и В1С . 8. В вазе лежат яблоки: 12 желтых и 6 красных. Сколькими способами можно взять из вазы 2 желтых и 4 красных яблока? 5 вариант 1. Вычислите π log 2 cos . 4 2. Найдите область определения функции x5 f(x) . x 2 64 3. Решите уравнение log 6(x 2 5) log 6 4x . 4. Решите неравенство 7 2x 3 7 x 28 0 . 5. Банковская процентная ставка равна 9% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 59405 рублей. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ACD 1 равна 24,5 3 см 2 . Найдите: а) диагональ куба; б) площадь сечения куба плоскостью ABC 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =4, а АВ=ВС=2. Вычислите косинус угла между векторами D1 А и D1С . 8. В вазе лежат яблоки: 5 зеленых и 10 красных. Сколькими способами можно взять из вазы 3 зеленых и 2 красных яблока? 6 вариант 1. Вычислите π log 3 tg . 6 2. Найдите область определения функции 5x x 2 f(x) log 5 . x8 3. Решите уравнение 3x 2 5x 6 2x . 4. Решите неравенство 2 2x 5 2 x 36 0 . 5. Банковская процентная ставка равна 12% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 56448 рублей. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ABC 1 равна 25 2 см 2 . Найдите: а) диагональ куба б) площадь сечения куба плоскостью ACD 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =6, а АВ=ВС=3. Вычислите косинус угла между векторами D1 А и D1С . 8. В вазе лежат яблоки: 6 желтых и 12 красных. Сколькими способами можно взять из вазы 4 желтых и 2 красных яблока? 7 вариант 1. Вычислите π log 2 sin . 4 2. Найдите область определения функции f(x) 25 x 2 . x 7 3. Решите уравнение log 3(10 x 2 ) log 3 3x . 4. Решите неравенство 6 2x 4 6 x 12 0 . 5. Банковская процентная ставка равна 8% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 40824 рубля. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ACD 1 равна 32 3 см 2 . Найдите: а) диагональ куба; б) площадь сечения куба плоскостью ABC 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =4, а АВ=ВС=2. Вычислите косинус угла между векторами AD1 и AB1 . 8. В вазе лежат яблоки: 5 зеленых и 10 красных. Сколькими способами можно взять из вазы 2 зеленых и 3 красных яблока? 8 вариант 1. Вычислите π log 3 ctg . 3 2. Найдите область определения функции x 6 f(x) log 5 2 . x 3x 3. Решите уравнение 15x 2 x 12 4x . 4. Решите неравенство 3 2x 6 3 x 27 0 . 5. Банковская процентная ставка равна 11% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 73926 рублей. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ABC 1 равна 36 2 см 2 . Найдите: а) диагональ куба б) площадь сечения куба плоскостью ACD 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =6, а АВ=ВС=3. Вычислите косинус угла между векторами AD1 и AB1 . 8. В вазе лежат яблоки: 6 желтых и 12 красных. Сколькими способами можно взять из вазы 2 желтых и 4 красных яблока? 9 вариант 1. Вычислите π log 2 tg . 4 2. Найдите область определения функции x 6 f(x) . x 2 81 3. Решите уравнение log 5(x 2 8) log 5 2x . 4. Решите неравенство 8 2x 5 8 x 24 0 . 5. Банковская процентная ставка равна 7% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 80143 рубля. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ACD 1 равна 40,5 3 см 2 . Найдите: а) диагональ куба; б) площадь сечения куба плоскостью ABC 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =4, а АВ=ВС=2. Вычислите косинус угла между векторами CD1 и CB1 . 8. В вазе лежат яблоки: 8 зеленых и 6 красных. Сколькими способами можно взять из вазы 4 зеленых и 2 красных яблока? 10 вариант 1. Вычислите π log 3 ctg . 4 2. Найдите область определения функции 4x x 2 f(x) log 5 . x9 3. Решите уравнение 8x 2 4x 5 3x . 4. Решите неравенство 2 2x 3 2 x 40 0 . 5. Банковская процентная ставка равна 9% годовых. Какова должна быть первоначальная сумма вклада, чтобы через 2 года его размер составил 47524 рубля. 6. Площадь сечения куба ABCDA 1 B 1 C 1 D 1 плоскостью ABC 1 равна 49 2 см 2 . Найдите: а) диагональ куба б) площадь сечения куба плоскостью ACD 1 . 7. Дан прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 , в котором А A 1 =6, а АВ=ВС=3. Вычислите косинус угла между векторами CD1 и CB1 . 8. В вазе лежат яблоки: 6 желтых и 8 красных. Сколькими способами можно взять из вазы 4 желтых и 2 красных яблока? ОТВЕТЫ № задания 1 1в -1 2в 0,5 2 7;4 7; ;2 0;6 3 1 2 4 (1; ) (3; ) 5 6 7 8 25000 5 3 см, 25 2 см 2 0,8 1200 0,8 7425 15000 9 3 см, 40,5 3 см 2 3в -1 ;6 3;6 3 4в 0,5 7;0 3; 4 5в -1 6в -1 7в -1 8в -1 9в 0 10в 0 8;5 8; ;8 0;5 ;7 5;5 3;0 6; 9;6 9; ;9 0;4 5 1 2 3 4 5 (1; ) (2; ) (1; ) (2; ) (1; ) (2; ) (1; ) (3; ) 30000 6 3 см, 36 2 см 2 0,8 450 20000 8 3 см, 32 3 см 2 0,8 990 50000 7 3 см, 49 2 см 2 0,8 450 45000 5 3 см, 12,5 3 см 2 0,8 990 35000 8 3 см, 64 2 см 2 0,8 1200 60000 6 3 см, 18 3 см 2 0,8 7425 70000 9 3 см, 81 2 см 2 0,8 1050 0,8 420 40000 7 3 см, 24,5 3 см 2 Информационное обеспечение обучения (перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы) Основные источники: 1. В.А. Гусев и др. Математика для профессий и специальностей социально-экономического профиля – М.:ИЦ «Академия». 2013. 2. Богомолов Н. В., Сб. дидактических заданий по математике: учеб. пособие для среднего профобразования/Н.В. Богомолов, Л.Ю. Сергиенко. -3-е изд., стер. - [б.м.]: Дрофа, 2009. - 236 с. - (Среднее проф.образование). 3. Богомолов Н. В., Сб. задач по математике: учеб. пособие для среднего профобразования/Н.В. Богомолов. -6-е изд., стер. - [б.м.]: Дрофа, 2010. - 205 с. - (Среднее проф.образование). 4. Л.С.Атанасян и др. Геометрия, 10-11классы. – М.: Просвещение, 2011. 5. А.Г.Мордкович Алгебра и начала анализа, 10-11 классы – Мнемозина 2011. Дополнительные источники: 1. Колягин Ю.М. и др. Математика (Книга 1). - М., 2003. 2. Колягин Ю.М. и др. Математика (Книга 2). - М., 2003. 3. Яблонский СВ. Введение в дискретную математику. Учебное пособие. -М.: Высшая школа 2002. 4. Омельченко В.Т., Курбатова Э.В. Математика. Феникс 2005. 5. Пакет прикладных программ по курсу математики ОС Windows XP, MS Office. Интернет-источники: 1. http://www.exponenta.ru/educat/links/l_educ.asp#0 – Полезные ссылки на сайты математической и образовательной направленности: Учебные материалы, тесты 2. http://www.fxyz.ru/ - Интерактивный справочник формул и сведения по алгебре, тригонометрии, геометрии, физике. 3. http://maths.yfa1.ru - Справочник содержит материал по математике (арифметика, алгебра, геометрия, тригонометрия). 4. allmatematika.ru - Основные формулы по алгебре и геометрии: тождественные преобразования, прогрессии, производная, стереометрия и проч. 5. http://mathsun.ru/ – История математики. Биографии великих математиков.