Определенный интеграл. Формула Ньютона - Лейбница
реклама

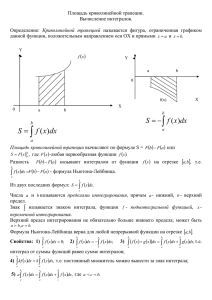
Определенный интеграл. Формула Ньютона - Лейбница 𝑦 Криволинейная трапеция 𝑆𝑘 = 𝑓(𝑥𝑘 ) ⋅ ∆𝑥𝑘 ∆𝑥𝑘 − длина отрезка [𝑥𝑘 ; 𝑥𝑘+1 ] 𝑆𝑛 = 𝑓0 ∆𝑥0 + 𝑓1 ∆𝑥1 + 𝑓2 ∆𝑥2 + + ⋯ + 𝑓𝑘 ∆𝑥𝑘 + ⋯ + 𝑓𝑛−1 ∆𝑥𝑛−1 𝑥0 = 𝑎, 𝑥𝑛 = 𝑏, ∆𝑥0 = ∆𝑥1 = ⋯ = ∆𝑥𝑛 𝑎 0 𝑏 𝑥1 𝑥2 𝑥𝑘 𝑥𝑘+1 𝑥𝑛−1 𝑥 𝑺 = 𝐥𝐢𝐦 𝑺𝒏 𝒏→∞ 𝑥1 𝑥2 𝑥𝑘 𝑥𝑘+1 𝑎 = 𝑥0 𝜌 = 𝜌(𝑥) 𝜌 = 𝜌(𝑥𝑘 ) 𝑥𝑛−1 𝑏 = 𝑥𝑛 𝑚 = 𝑉𝜌 𝑚 = 𝑆𝜌 𝑚 = 𝑙𝜌 𝑚𝑘 ≈ 𝜌(𝑥𝑘 )∆𝑥𝑘 ∆𝑥𝑘 − длина отрезка [𝑥𝑘 ; 𝑥𝑘+1 ] 𝑚 ≈ 𝑆𝑛 = 𝑚0 + 𝑚1 + 𝑚2 + ⋯ + 𝑚𝑘 + ⋯ + 𝑚𝑛−1 = = 𝜌 𝑥0 ∆𝑥0 + 𝜌 𝑥1 ∆𝑥1 + ⋯ + 𝜌 𝑥𝑛−1 ∆𝑥𝑛−1 𝒎 = 𝐥𝐢𝐦 𝑺𝒏 𝒏→∞ 𝑡1 𝑡2 𝑡𝑘 𝑎 = 𝑡0 𝑣 = 𝑣(𝑡) 𝑡𝑘+1 𝑡𝑛−1 𝑏 = 𝑡𝑛 𝑆 = 𝑣𝑡 𝑺 = 𝐥𝐢𝐦 𝑺𝒏 𝒏→∞ 𝑣 = 𝑣(𝑡𝑘 ) 𝑠𝑘 ≈ 𝑣(𝑡𝑘 )∆𝑡𝑘 ∆𝑡𝑘 − длина отрезка [𝑡𝑘 ; 𝑡𝑘+1 ] 𝑠 ≈ 𝑆𝑛 = 𝑠0 + 𝑠1 + 𝑠2 + ⋯ + 𝑠𝑘 + ⋯ + 𝑠𝑛−1 = = 𝑣 𝑡0 ∆𝑡0 + 𝑣 𝑡1 ∆𝑡1 + ⋯ + 𝑣 𝑡𝑛−1 ∆𝑡𝑛−1 𝒔 = 𝐥𝐢𝐦 𝑺𝒏 𝒏→∞ 𝒎 = 𝐥𝐢𝐦 𝑺𝒏 𝒏→∞ Математическая модель: 1. Разбиваем отрезок [𝑎; 𝑏] на 𝑛 равных частей. Определенный интеграл от функции 𝒚 = 𝒇(𝒙) по 2. Составляем сумму 𝑆𝑛 . отрезку [𝒂; 𝒃] 3. Находим lim 𝑆𝑛 . 𝑛→∞ 𝒃 𝐥𝐢𝐦 𝑺𝒏 = 𝒏→∞ Верхний предел интегрирования 𝒇 𝒙 𝒅𝒙 𝒂 Нижний предел интегрирования Древний Египет 1800 год доАрхимед н. э. Евдокс Книдский ок. 408 год до н. э. – ок. 355 год до н. э. 287 год до н. э. – 212 год до н. э. Древний Китай III век н. э. Абу Али аль-Хасан ибн аль-Хасан ́ ́ ́ ибн аль-Хайса́м аль-Басри́ 965 год – 1040 год ́ Бонавентура Франческо Кавальери 1598 год – 1647 год Пьер де Ферма 1601 год – 1665 год Исаак Барроу 1630 год – 1677 год Эванджелиста Торичелли 1608 год – 1647 год Исаак Ньютон 1642 год – 1727 год Готфрид Вильгельм Лейбниц 1646 год – 1716 год ſ − длинная S, сокращение латинского слова «сумма» 𝑏 𝑎 Жан Батист Жозеф Фурье 1642 год – 1830 год 𝑏 𝑓 𝑥𝑺𝒏𝑑𝑥 𝑺 = 𝐥𝐢𝐦 𝒏→∞ 𝑎 Геометрический смысл определенного интеграла 𝑏 𝒔 = 𝐥𝐢𝐦 𝑣 𝑡𝑺𝑑𝑡 𝒏 𝑏 𝜌 𝑥𝑺𝒏𝑑𝑥 𝒎 = 𝐥𝐢𝐦 𝒏→∞ 𝑎 𝒏→∞ 𝑎 Физический смысл определенного интеграла 𝑎 𝑏 𝑏 𝑠= 𝑣 𝑡 𝑑𝑡 𝒃 𝑎 𝑣 𝑡 = 𝑠 ′ 𝑡 ⇒ 𝑠 𝑡 − первообразная для 𝑣 𝑡 ⇒ ⇒ ⇒ 𝑠 = 𝑠 𝑏 − 𝑠(𝑎) 𝒗 𝒕 𝒅𝒕 = 𝒔 𝒃 − 𝒔(𝒂) 𝒂 Теорема. Если функция 𝑦 = 𝑓(𝑥) непрерывна на отрезке [𝑎; 𝑏], то справедлива формула 𝒃 𝒂 Двойная подстановка 𝒃 𝒇 𝒙 𝒅𝒙 = 𝑭(𝒙) 𝑭 𝒃 − 𝑭(𝒂) 𝒂 𝐹(𝑥) – первообразная для 𝑓(𝑥) Формула Ньютона-Лейбница Пример: Вычислить 3 3 𝑥 𝑑𝑥. −1 Решение: 𝑏 𝑓 𝑥 𝑑𝑥 = 𝐹(𝑥) 𝑎 𝑥4 4 3 −1 ′ = 𝑥3 𝑏 𝑎 𝑥4 ⇒𝐹 𝑥 = 4 4 3 3 −1 𝑥 3 𝑑𝑥 = 𝐹 𝑥 = 𝐹 3 − 𝐹 −1 = − −1 4 4 4 = 81 1 − = 20 4 4 Пример: Вычислить площадь фигуры, ограниченной линиями 𝑦 = Решение: 8 3 𝑆= 𝑥, 𝑦 = 0, 𝑥 = 8. 𝑦 𝑥𝑑𝑥 0 𝑏 𝑓 𝑥 𝑑𝑥 = 𝐹(𝑥) 𝑎 1 𝑥 3+1 1 +1 3 3 𝑏 𝑎 ′ = 3 𝑥⇒𝐹 𝑥 = 8 0 3 𝑥𝑑𝑥 = 𝐹 𝑥 33 4 𝑥 4 8 33 4 33 4 =𝐹 8 −𝐹 0 = 8 − 0 = 12 0 4 4 0 8 𝑥 Свойство 1. Интеграл от суммы функций равен сумме интегралов: 𝒃 𝒃 𝒇 𝒙 + 𝒈(𝒙) 𝒅𝒙 = 𝒂 𝒃 𝒇 𝒙 𝒅𝒙 + 𝒂 𝒈 𝒙 𝒅𝒙 𝒂 Доказательство. Если 𝐹 𝑥 − первообразная для 𝑓(𝑥), а G 𝑥 − первообразная для 𝑔(𝑥), то 𝐹 𝑥 + 𝐺 𝑥 − первообразная для 𝑓 𝑥 + 𝑔(𝑥). Тогда 𝑏 𝑓 𝑥 + 𝑔(𝑥) 𝑑𝑥 = 𝐹 𝑥 + 𝐺(𝑥) 𝑎 = 𝐹 𝑏 + 𝐺(𝑏) − 𝐹 𝑎 + 𝐺 𝑎 = 𝐹 𝑏 −𝐹 𝑎 𝑏 = 𝑏 𝑓 𝑥 𝑑𝑥 + 𝑎 𝑔 𝑥 𝑑𝑥 𝑎 𝑏 = 𝑎 + 𝐺 𝑏 −𝐺 𝑎 = Пример: Вычислить 2 1 1 𝑒 𝑥 + 𝑥 𝑑𝑥. Решение: 𝑏 𝑏 𝑓 𝑥 + 𝑔(𝑥) 𝑑𝑥 = 𝑎 𝑒 𝑥 ′ 𝑓 𝑥 𝑑𝑥 + 𝑎 𝑥 𝑏 =𝑒 ⇒𝐹 𝑥 =𝑒 1 ′ ln 𝑥 = ⇒ 𝐺 𝑥 = ln 𝑥 𝑥 2 2 1 𝑥 𝑒 + 𝑑𝑥 = 𝑒 𝑥 𝑑𝑥 + 𝑥 1 = 𝑒 2 − 𝑒 1 + ln 2 1 𝑔 𝑥 𝑑𝑥 𝑎 𝑥 2 1 𝑏 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 = 𝐹(𝑥) 𝑎 1 2 2 𝑑𝑥 = 𝐹 𝑥 +𝐺 𝑥 = 𝑒 2 − 𝑒 1 + ln 2 − ln 1 = 𝑥 1 1 Свойство 2. Постоянный множитель можно вынести за знак интеграла 𝒃 𝒃 𝒌𝒇(𝒙)𝒅𝒙 = 𝒌 𝒂 𝒇 𝒙 𝒅𝒙 𝒂 Пример: Вычислить 22 𝑑𝑥. 1 𝑥 Решение: 𝑏 𝑏 𝑘𝑓(𝑥)𝑑𝑥 = 𝑘 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 𝑎 𝑎 𝑏 𝑓 𝑥 𝑑𝑥 = 𝐹(𝑥) 𝑎 1 ⇒ 𝐹 𝑥 = ln 𝑥 𝑥 2 2 2 1 2 𝑑𝑥 = 2 𝑑𝑥 = 2 ⋅ 𝐹 𝑥 = 2 ⋅ ln 2 − ln 1 = 2 ln 2 = ln 4 𝑥 𝑥 1 ln 𝑥 1 ′ = 1