0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Ответ: 0,4

Задачи по теории
вероятностей
В10 (2)
Простейшие вероятностные задачи:
N ( A)
P ( A) 
N
N - общее число элементарных событий
N(A) - число элементарных событий,
благоприятствующих событию А
На клавиатуре телефона 10 цифр (от 0 до 9).
Какова вероятность того, что случайно нажатая
цифра будет четной?
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
4
P ( A) 
 0,4
10
Ответ: 0,4
Какова вероятность того, что случайно
выбранное натуральное число от 10 до 19
делится на три?
10, 11, 12, 13, 14, 15, 16, 17, 18, 19
3
P( A) 
 0,3
10
Ответ: 0,3
Перед началом футбольного матча судья бросает монету,
чтобы определить, какая из команд начнет игру с мячом.
Команда «Физик» играет три матча с разными
командами. Найдите вероятность того, что в этих играх
«Физик» выиграет жребий ровно два раза.
Ф/1 ОР
ОР
ОР
ОР
РО
РО
РО
РО
Ф/2 ОР
ОР
РО
РО
ОР
ОР
РО
РО
Ф/3 ОР
РО
ОР
РО
ОР
РО
ОР
РО
3
P ( A)   0,375
8
Ответ: 0,375
Правило умножения
Для того чтобы найти число всех возможных
исходов независимого проведения двух
испытаний А и В, следует перемножить
число всех исходов испытания А и число
всех исходов испытания В.
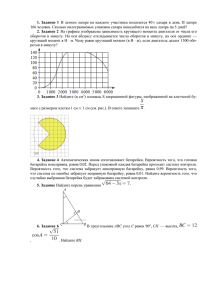
Задача 4. В случайном эксперименте бросают два
игральных кубика. Найдите вероятность того, что в
сумме выпадет 4 очка. Результат округлите до сотых.
Решение:
Множество элементарных исходов: N= 6*6=36
Числа на
выпавших
сторонах
1
2
1
2
3
4
5
6
2
3
4
5
6
7
3 4
4 5
5 6
6 7
7 8
8 9
3
4
5
5
6
7
8
9
10
6
7
8
9
10
11
6
A= {сумма равна 4}
7 N(А)=3
N ( A)
8
P ( A) 
N
9
3
P ( A) 
10
36
11
12
Ответ:0,08
Задача 5. В случайном эксперименте монету бросили три
раза. Какова вероятность того, что орел выпал ровно
два раза.
Решение: Множество элементарных исходов: N=2*2*2=8
1
бросок
2
бросок
3
бросок
О
О
О
О
Р
Р
Р
Р
О
О
Р
Р
О
О
Р
Р
О
Р
О
Р
О
Р
О
Р
A= {орел выпал ровно 2 } N(А)=3
N ( A) 3
P( A) 
  0,375
N
8
8 исходов
Ответ: 0,375
1
2
3
4
О
О
О
О
О
О
О
Р
О
Р
О
О
О
Р
О
Р
О
Р
Р
О
О
Р
Р
Р
Р
О
О
О
Р
О
О
Р
Р
О
Р
О
Р
О
Р
Р
Р
Р
О
О
Р
Р
О
Р
Р
Р
Р
О
Р
Р
Р
Р
Монету бросают четыре
вероятность того,
О
О раза.Р Найдите
О
что орел выпадет ровно
три раза.
О
О
Р
Р
4
P ( A) 
 0,25
16
Ответ: 0,25
Несовместные события – это события, которые не
наступают в одном опыте.
À  Â (объединение)
À Â
А В
À Â
–
событие,
состоящее
из
элементарных исходов, благоприятствующих хотя
бы одному из событий А,В
(пересечение)
–
событие,
состоящее
из
элементарных исходов, благоприятствующих обоим
событиям А и В.
Определение: Суммой А и В называют событие,
которое наступает тогда и только тогда, когда
наступает хотя бы одно из двух событий.
Вероятность суммы несовместных событий
равна сумме вероятностей этих событий
Ð À  Â  Ð À  ÐÂ
Определение: Произведением А и В называют
событие, которое наступает тогда и только тогда, когда
наступает событие А, и событие В.
Вероятность
произведения
независимых
событий равна произведению вероятностей
этих событий
Ð À  Â  Ð À ÐÂ
Вариант 20
В10.
Автоматическая
линия
изготавливает
батарейки. Вероятность того, что готовая батарейка
неисправна, равна 0,02. Перед упаковкой каждая
батарейка проходит систему контроля. Вероятность
того, что система забракует неисправную батарейку,
равна 0,99. Вероятность того, что система по ошибке
забракует исправную батарейку, равна 0,01. Найдите
вероятность того, что случайно выбранная из
упаковки батарейка будет забракована.
1- 0,02= 0,98
Батарейка будет забракована:
А= {батарейка неисправна и забракована справедливо}
В={батарейка исправна и забракована ошибочно}
Батарейка будет забракована: Несовместные события
А= {батарейка неисправна и забракована справедливо}
В={батарейка исправна и забракована ошибочно}
Несовместные события – это события, которые не
наступают в одном опыте.
Формула сложения для несовместных событий:
Ð À  Â  Ð À  ÐÂ
Ð À  0,02  0,99
ÐÂ  0,01 0,98
Ответ: 0,0296
Вариант 21
В10. Вероятность того, что батарейка
бракованная, равна 0,06. Покупатель в
магазине выбирает случайную упаковку, в
которой две таких батарейки. Найдите
вероятность того, что обе батарейки
окажутся исправными.
Р(батарейка исправна) = 1 – 0,06 = 0,94
Вероятность
произведения
независимых событий равна
произведению вероятностей
этих событий
Ð À  Â  Ð À ÐÂ
Ð  0,94  0,94
Ответ: 0,8836
В10. На рисунке изображён лабиринт. Паук заползает в
лабиринт в точке «Вход». Развернуться и ползти назад паук не
может, поэтому на каждом разветвлении паук выбирает один
из путей, по которому ещё не полз. Считая, что выбор
дальнейшего пути чисто случайный, определите, с какой
вероятностью паук придёт к выходу D .
?
?
?
?
Вероятность выбора пути
на развилке равна: один из
двух
1
Ð
2
 0,5
4


Ð  0,5  0,5  0,5  0,5  0,5
Ответ: 0,0625
4 развилки
Выбор пути на развилках - события
независимые
Вариант 23
В10 На рисунке изображён лабиринт. Паук заползает
в лабиринт в точке «Вход». Развернуться и ползти
назад паук не может. На каждом разветвлении паук
выбирает путь, по которому ещё не полз. Считая
выбор дальнейшего пути случайным, определите, с
какой вероятностью паук придёт к выходу А.
Выбор пути движения - события
несовместны
Ð  Ð1  Ð2
Ð1  0,5
3
?
Ð2  0,5
5
?? ?
?? ??
Ð  0,125  0,03125
Ответ: 0,15625
Вариант 24
В10 Всем пациентам с подозрением на гепатит делают анализ
крови. Если анализ выявляет гепатит, то результат анализа
называется положительным. У больных гепатитом пациентов
анализ даёт положительный результат с вероятностью 0,9. Если
пациент не болен гепатитом, то анализ может дать ложный
положительный результат с вероятностью 0,01. Известно, что 5%
пациентов, поступающих с подозрением на гепатит, действительно
больны гепатитом. Найдите вероятность того, что результат анализа
у пациента, поступившего в клинику с подозрением на гепатит,
будет положительным.
Анализ положителен: Несовместные события
А= {болен гепатитом, анализ верен}
1-0,05= 0,95
В={не болен гепатитом, анализ ложен}
Вероятность суммы несовместных событий равна
сумме вероятностей этих событий
Ð À  Â  Ð À  ÐÂ
Ð À  Â  Ð À  ÐÂ
Ð À  0,9  0,05
ÐÂ  0,01 0,95
Ð À  Â  0,045  0,0095  0,0545
Ответ: 0,0545
Вариант 25
В10 Из районного центра в деревню ежедневно ходит
автобус. Вероятность того, что в понедельник в
автобусе окажется меньше 20 пассажиров, равна 0,94.
Вероятность того, что окажется меньше 15 пассажиров,
равна 0,56. Найдите вероятность того, что число
пассажиров будет от 15 до 19.
А= {в автобусе < 15}
Несовместные события
В={ в автобусе от 15 до 19}
(А + В) – хотя бы одно выполняется (объединение)
Ð À  Â  Ð À  ÐÂ
ÐÂ  Ð À  Â  Ð À
Ответ: 0,38
Перестановки
Перестановкой называется множество из n
элементов, записанных в определённом порядке.
Теорема о перестановках элементов конечного
множества: n
различных элементов можно
расставить по одному на n различных мест
ровно n! способами.
Ðn  1 2  3  ...  n  n!
Найдите
количество всех способов,
которыми можно составить трехцветный
флаг из горизонтальных полос красного,
белого и синего цветов.
Ð3  1 2  3  6
В 6 классе в среду 6 уроков: математика,
литература, русский язык, английский
язык, биология и физкультура. Сколько
вариантов расписания можно составить?
Расставляем предметы по порядку
Предмет
Число вариантов
6
Математика
Литература
Русский язык
Английский язык
Биология
Физкультура
5
4
3
2
1
Всего вариантов
расписания
Ð6  6!
1•2•3•4•5•6=720
Размещения
Размещением
называется
расположение
“предметов” на некоторых “местах” при условии,
что каждое место занято в точности одним
предметом и все предметы различны.
В размещении учитывается порядок следования
предметов. Так, например, наборы (2,1,3) и (3,2,1)
являются различными
Число всех выборов k элементов из n
данных с учетом их порядка называют
размещением из n элементов по k
n
!
k
Àn 
( n  k )!
Сколько двузначных чисел можно
составить из цифр 1,2,3,4?
1 2  3  4
4!
À 

(4  2)!
1 2
2
4
Ответ: 12
Сколько трёхзначных чисел можно
составить из цифр 4,5,6,7,8?
3
5
À
5!

(5  3)!
 60
Ответ: 60
Завучу школы из 8 предметов: алгебра,
геометрия, информатика, физика, химия,
ОБЖ, литература, физическая культура
необходимо составить расписание на один
день из 5 уроков. Сколькими способами
можно это сделать?
8!
 6720
A 
(8  5)!
5
8
Ответ: 6720
29
Сочетания
Число всех выборов k элементов из n данных
без учета порядка называют числом сочетаний
из n элементов по k
k
k
n
A

Ñ k!
n
n!
Ñ n  k!n  k !
k
«Проказница Мартышка, Осел, Козел, да
Косолапый Мишка затеяли сыграть
квартет». Мишке поручили выбрать 4
любых инструмента из 7 имеющихся.
Найти
число
возможных
выборов
инструментов.
4!5  6  7 5  6  7
7!
Ñ 7  4!7  4!  4!3!  1 2  3
4
Ответ: 35
N ( A)
P ( A) 
N
Вариант 26
В10 У мальчика есть 8 шариков – 6 белых и 2 красных.
Он раскладывает их наугад в две коробочки по 4
шарика. Найдите вероятность того, что красные
шарики окажутся в разных коробочках. Ответ
округлите до сотых.
А= {красные в разных коробочках}
Из 8 шаров случайным
образом выбор 4 шаров
N  C8
4
C
4
8
8!

4!(8  4)!
C N ( A)  C 6  C 2
Из 2 красных шаров 1 шар можно выбрать C
Ответ: 0,57
3
Из 6 белых шаров 3 шара можно выбрать
6
1
2
3
1
Вариант 27
В10 При изготовлении подшипников диаметром 67 мм
вероятность того, что диаметр будет отличаться от
заданного меньше, чем на 0,01 мм, равна 0,965. Найдите
вероятность того, что случайный подшипник будет
иметь диаметр меньше чем 66,99 мм или больше чем
67,01 мм.
А = {диаметр отличается < на 0,01} P( A)  0,965
À  {диаметр < 66,99
или > 67,01}
Противоположное
Вероятности противоположных событий: событие

Ð À  Ð À  1

Ð À  1  Ð À
P( A)  1  0,965  0,035
Ответ: 0,035
Вариант 28 Ð À  Â  Ð À  ÐÂ
В10. Вероятность того, что на тесте по биологии
учащийся О. верно решит больше 11 задач, равна
0,67. Вероятность того, что О. верно решит больше 10
задач, равна 0,74. Найдите вероятность того, что О.
верно решит ровно 11 задач.
События А и В
несовместные
А = {О. решит верно 11 задач}
В = {О. решит верно > 11 задач} P ( Â )  0,74
Несовместные события – это события, которые не
наступают в одном опыте.
А+В ={О. решит верно > 10 задач} P ( A  Â)  0,67
P( A)  0,74  0,67  0,07
Ответ: 0,07