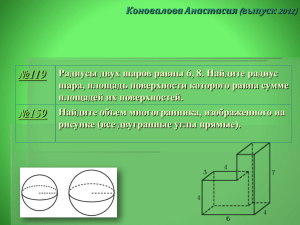
класс, подготовка к ЕГЭ 11
реклама

11 класс, подготовка к ЕГЭ Подготовила: Ефимова Людмила Иосифовна, учитель математики МБОУ «СОШ №9» высшая квалификационная категория Задачи, решаемые при помощи графика линейной функции (прямой): тепловое расширение рельса; месячная прибыль предприятия. Задачи, решаемые при помощи графика квадратичной функции (параболы): мальчик, камешки, колодец; выручка предприятия при наибольшей цене; мяч, подброшенный вверх; скорость вращения ведёрка; частичное вытекание воды из бака; полное вытекание воды из бака; Задачи, решаемые при помощи графика квадратичной функции (параболы): камнеметательная машина; нагревание прибора; время проверки работы лебёдки; мотоциклист в зоне сотовой связи; торможение автомобиля; момент инерции вращающейся катушки. Задание B11 Деталью некоторого прибора является вращающаяся катушка. Она состоит из трёх однородных соосных цилиндров: центрального массой m = 8 кг и радиуса R = 5 см, и двух боковых с массами M = 2 кг и с радиусами R + h. При этом момент инерции катушки относительно оси вращения, выражаемый в кг· см2 , даётся формулой (m+2M)R2 . + h2). I = + M(2Rh 2 При каком максимальном значении h момент инерции катушки не превышает предельного значения 1900 кг· см2 ? Ответ выразите в сантиметрах. Задание B11 Решение. Функция: Данные: m 8, M 2, R 5. hmax 0 при I 1900. 2 (m 2M ) R 2 I M (2 Rh h ). 2 2 I 2h 20h 150, h 0. Найти: hмах Схематичный график: y y = I(h) 1900 150 0 hmax h Задание B11 2 2h 20h 150 1900 Решение. 2h 2 20h 1750 0, |: 2 Решаем 2 h 10h 875 0. уравнение: 2 2 D 10 4 875 60 . h1 35,h2 25 hmax . (больший корень) y y = I(h) 1900 Ответ: 25. 150 0 hmax h Задание B11 Автомобиль, движущийся в начальный момент времени со скоростью v0 = 24 м/с, начал торможение с постоянным ускорением a = 3 м/с2. За t секунд после начала at2 торможения он прошёл путь S = v0t (м). Определите 2 время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 90 метров. Ответ выразите в секундах. Задание B11 Функция: Данные: v0 24, a 3. at 2 S v0t . 2 Найти: t 0 при S 90. Схематичный график: y y = S(t) 90 tнаим. 0 t Задание B11 Решение. Функция: Решаем уравнение: 2 3t S 24t . 2 2 3t 90 24t . 2 3 2 3 t 24t 90 0, |: 2 2 2 t 16t 60 0. t1 10, t2 6 tнаим. ( меньший корень) Ответ: 6. Схематичный график: y y = S(t) 90 tнаим. 0 t Задание B11 Мотоциклист, движущийся по городу со скоростью v0 = 57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a = 12 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением at2 S = v0t . Определите наибольшее 2 время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах. Нет зоны действия сети Задание B11 2 at . Функция: S v0t Данные: v0 57, a 12. 2 tнаиб. 0 при S 30. Найти: 57t 6t 30 2 6t 2 57t 30 0, |: 3 2 2t 19t 10 0. t1 10, t2 0,5(ч) tнаиб. (больший корень ) tнаиб. 30( мин.) Ответ: 30 Схематичный график: y y = S(t) 30 tнаиб. t 0 Задание B11 Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением T(t) = T0 + bt + at2 , где t — время в минутах, T0 = 1450 К, a = - 12,5 К/мин2 , b = 175 К/мин. Известно, что при температуре нагревателя свыше 1750 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах. Пирометр — прибор для беcконтактного измерения температуры тел. Задание B11 Функция: Данные: T0 1450, a 12,5, b 175. T (t ) T0 bt at 2 Найти: tнаиб. 0 при T (t ) 1750. Схематичный график: y 1750 1450 0 y = T(t) tнаиб. Необходимо отключить t Задание B11 2 Решение. Функция: T (t ) 1450 175t 12,5t Решаем Найти: tнаиб. 0 при T (t ) 1750. уравнение: 2 Схематичный 1750 1450 175t 12,5t график: 2 12,5t 175t 300 0, |: 12,5 t 14t 24 0, t1 12, t 2 2 t наиб. y 1750 ( меньший корень ) 1450 2 Ответ: 2. 0 y = T(t) tнаиб. Необходимо отключить t Задание B11 Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полёта камня описывается формулой y = ax2 + bx , -1 -1 7 где a м ,b — постоянные параметры, 60 6 x (м) — смещение камня по горизонтали, y (м) — высота камня над землёй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 9 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра? Задание B11 Данные: Функция: y( x) ax bx. 1 a , 60 7 b . 6 Найти: x при y ( x) 10. 2 Схематичный график: y y = y(x) 10 xнаиб. 0 x Задание B11 Решение. Решаем уравнение: 1 2 7 Функция: y ( x) 60 x 6 x. Найти: x при y ( x) 10. Схематичный график: 1 2 7 x x 10. 60 6 2 x 70 x 600 0, x1 10, x2 60 x наиб. Ответ: 60. y y = y(x) 10 xнаиб. 0 x Задание B11 В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону H(t) = H0 + bt + at2 , где Н0 = 2 м — начальный уровень воды, 1 -2 2 a м/мин , b м/мин, t — время в минутах, 50 5 прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах. H 0 Задание B11 Данные: Функция: H 0 2 м, 1 a , 50 2 b . 5 Найти: Н (t ) H 0 bt at 2 t при H (t ) 0. Схематичный график: y 2 H=0 0 y = H(t) t tвытекания Задание B11 2 1 2 Функция: Н (t ) 2 t t 5 50 Найти: t при H (t ) 0. Решение. Решаем уравнение: 2 1 2 2 t t 0, 5 50 Схематичный график: y 2 100 20t t 0, 2 t 10 2 Ответ: y = H(t) 0 t 10. 10. H=0 0 t tвытекания Задание B11 В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону g 22 H (t ) = H0 — 2gH 0 kt k t , где t — время в секундах, 2 прошедшее с момента открытия крана, k = 1 — 200 отношение площадей поперечных сечений крана и бака, Н0 = 5 м — начальная высота столба воды, а g — ускорение свободного падения (считайте g = 10 м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды? Задание B11 g 22 Данные: Функция: Н (t ) H 0 2 gH 0 kt k t 2 2 g 10 м / с , 1 5 Найти: t при H (t ) H 0 . 1 4 4 k , 200 Схематичный график: H0 5 м y 5 H0 1 H0 4 1 H0 4 0 y = H(t) t tнаим. Задание B11 1 1 2 Решение. Функция: Н (t ) 5 t t 20 8000 Решаем уравнение: 1 1 2 5 5 t t . 20 8000 4 Схематичный график: 40000 400t t 10000. t 2 400t 30000 0. y 5 2 y = H(t) t1 300, t2 100 t наим. Ответ: 100. 1 H0 4 0 t tнаим. Задание B11 Если достаточно быстро вращать ведёрко с водой на верёвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведёрка сила давления воды на дно не остаётся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила её давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная v2 g , где m — масса воды в в ньютонах, равна P m L килограммах, v — скорость движения ведёрка в м/с, L — длина верёвки в метрах, g — ускорение свободного падения (считайте, g = 10 м/с2 ). С какой наименьшей скоростью надо вращать ведёрко, чтобы вода не выливалась, если длина верёвки равна 62,5 cм? Ответ выразите в м/с. Задание B11 Данные: L 62,5 см 0,625 м v2 Функция: P m g L Найти: vнаим. 0 при P 0. Схематичный график: y y = P(v) v Pmax = P ≥ 0 Pmin > 0 0 vнаим. -10m Задание B11 Решение. v2 Функция: P m 10 , m 0, v 0. 0,625 Решаем уравнение: v2 m 10 0, v 0. 0,625 v2 m 10 0, v 0, 0,625 Так как v 0, то v 2,5. Ответ: 2,5. Схематичный график: y y = P(v) v 0 vнаим. -10m Задание B11 Высота над землёй подброшенного вверх мяча меняется по закону h(t) = 1,4 + 9t - 5t2 , где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 3 метров? Функция: h(t ) 5t 9t 1,4 Найти: t t2 t1 2 5t 9t 1,4 3 t 1,6 0,2 1,4 2 5t 9t 1,4 3. 2 5t 9t 1,6 0, y 2 y = h(t) 3 1,4 ∆t 0 t1 t1 0,2, t1 1,6. Ответ: Данные: h(t ) 3 1,4. t t2 Задание B11 Зависимость объёма спроса q (тыс. руб.) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаётся формулой q = 130 - 10p . Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле r(p) = q · p. Определите наибольшую цену p, при которой месячная выручка составит не менее 360 тыс. руб. Ответ приведите в тыс. руб. Функция: q 130 10 p, r ( p) q p r ( p) (130 10 p) p Данные: r ( p) 360 0 Найти: pнаиб. при r ( p) 360. y y = r(p) 360 pнаиб. p Задание B11 Решение. r ( p) (130 10 p) p 2 r ( p) 10 p 130 p 10 p 130 p 360 2 10 p 130 p 360, 2 p 13 p 36 0, p1 4, p2 9 pнаиб. 9. 2 Ответ: 9. y y = r(p) 360 pнаиб. 0 p Задание B11 1,2 с 1,1 с После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле h = 5t2, где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 1,2 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,1 с? Задание B11 2 Решение. Функция: h 5t Данные: tдо 1,2 с, tизм. 1,1 с. h h(1,2) h(1,1) Найти: Схематичный график: h 5 1,2 5 1,1 2 2 y h(1,2) 5 (1,2 1,1 ) 5 (1,2 1,1) (1,2 1,1) ∆h 5 0,1 2,3 1,15( м) 2 2 y=h(t) h(1,1) Ответ: 1,15. 1,1 1,2 0 t Задание B11 Некоторая компания продает свою продукцию по цене p = 600 руб. за единицу, переменные затраты на производство одной единицы продукции составляют ν = 400 руб., постоянные расходы предприятия f = 600000 руб. в месяц. Месячная операционная прибыль (в рублях) вычисляется по формуле π(q) = q( p - ν)- f . Определите наименьший месячный объём производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 500000 руб. Задание B11 Функция: (q) q( p ) f Данные: p 600 руб., Найти: qнаим. при (q) 500000. 400 руб. f 600000 руб. Схематичный график: Решение. y (q) 200q 600000 y = π(q) 200q 600000 500000 500000 200q 1100000 qнаим. q qнаим. 5500 Ответ: 5500. 0 - 600000 Задание B11 При температуре 0oС рельс имеет длину lo= 20 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(to) = l0 ( 1+α·to), где α = 1,2·10-5(oC)-1 – коэффициент теплового расширения, to - температура (в градусах Цельсия). При какой температуре рельс удлинится на 9 мм? Ответ выразите в градусах Цельсия. y 20009 Функция: 0 0 l (t ) l0 l0 t y=l(to) Найти: t при l (t ) 20009 мм 0 20000 0 0 to to Задание B11 Решение. l0 2 104 мм; 1,2 105 (0C )1. l0 20 м 20 100см 2000 10 мм 4 20000 мм 2 10 мм 5 0 l (t ) 20000 2 10 1,2 10 t 0 4 l (t ) 0,24 t 20000 0 y 20009 0 20009 0,24 t 20000 9 0,24 t 0 0 0 t 37,5 С y=l(to) 0 Ответ: 37,5. 20000 0 to to