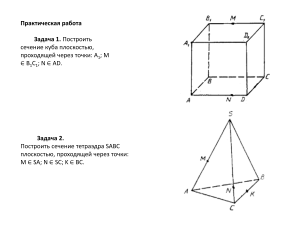
Задача №2. Симанов, Зайсанов.

Сечение тетраэдра
Выполнили: Ученики 11 «М» класса
Симанов Д.В.
Зайсaнов В.А.
Задача
• Дан произвольный тетраэдр ABCS.
AM:MS=3:2. SN:NC=4:1. CP=PB.
• Построить: сечение.
• Найти: Как сечение делит
пересеченные стороны.
Решение при помощи теоремы ЧевыМенелая
S
2x
4y
M
3x
N
А
y
C
L
B
Z
P
Z
K
1
6
CK
KA
M
3x
1
S
CK
KA
2x
4y
1
N
y
А
C
K
5d
A
C
1
1
6
d K
z
z
L
B
P AL
LB
6
1
Ответ: 6:1
Решение при помощи метода
апликат
1) Достроим сечение.
2) ] (MNP) = (XOY).
3) ] Zs = 4
Тогда
4) ZA = -6
5) ZC = -1
А значит,
6) ZB = 1
Откуда следует (ZA = -6)
7) AL/LB= 6
2х
S (ZS = 4)
4y
M
3х
N
y
A
C
P
L
Ответ: 6.
B
z
(ZB = 1)
z
K
(ZC = -1)