rabota 2 - Всероссийский фестиваль педагогического

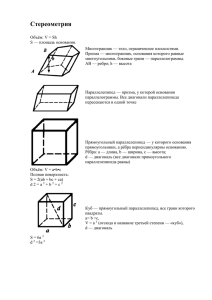
Всероссийский фестиваль педагогического творчества
(2015/2016 учебный год)
Номинация: Педагогические идеи и технологии: среднее
образование
Название работы: Разработка урока по геометрии на тему
«Многогранники» (10 класс)
Автор: Лихолетова Анастасия Сергеевна
Место выполнения работы: МБОУ Куйбышевская СОШ им.
А. А. Гречко с. Куйбышево, Ростовской области
Тема урока:
Цель урока
• рассмотреть понятие многогранника, его
элементов и виды, сформировать понятие
правильного многогранника
Давай те рассмотрим некоторые фигуры, которые нам уже известны?
Рис.2
Рис.1
Рис.3
Как называются фигура изображенные на рисунках 1-3?
На рисунке 1 изображен параллелепипед, на рисунке 2 тетраэдр, на рисунке 3
куб.
Рассмотрим каждую фигуру отдельно и охарактеризуем.
На рисунке изображен параллелепипед.
Из скольких граней состоит параллелепипед?
Параллелепипед состоит из 6 граней.
Какие фигуры представляют собой грани?
Грани параллелепипеда представляют собой
параллелограммы.
Хорошо. Сколько ребер в данной фигуре?
В данной фигуре 12 ребер.
Сколько вершин имеет параллелепипед?
У параллелепипеда 8 вершин.
Итак, параллелепипед составлен из
параллелограммов. А параллелограммам - это
четырехугольник, а если более общее, то
многоугольник.
Рис.1
Теперь охарактеризуем фигуру на рисунке 2, т.е. тетраэдр.
Рис.2
Сколько граней в тетраэдре?
У тетраэдра 4 грани.
Какими фигурами представлены грани?
Грани тетраэдра представляют собой
треугольники.
Сколько ребер в данной фигуре?
В тетраэдре 6 ребер.
Сколько вершин входят в тетраэдр?
Данная фигура имеет 4 вершины.
Какой можно сделать вывод?
Тетраэдр состоит из 4-х треугольников, которые
являются разновидностью многоугольника.
Хорошо, давайте охарактеризуем третью
фигуру.
На рисунке 3 изображен куб. Так же куб можно называть гексаэдр.
Сколько граней у куба?
У куба 6 граней.
Какими фигурами представлены грани?
Грани представляют собой квадраты.
Сколько ребер в данной фигуре?
В состав куба входят 12 ребер.
Сколько имеет данная фигура вершин?
В данной фигуре 8 вершин.
Какой мы сделаем вывод?
Данная фигура состоит из квадратов,
являющихся разновидностью
многогранника.
Рис.3
Мы рассмотрели фигуры составленные только из четырех угольников и
треугольников. А есть ли еще какие-то фигуры составленные из более сложных
фигур?
Давайте возьмем различных фигур и попробуем составить новые.
Например, возьмем шестиугольник, прямоугольник, треугольник и
параллелограмм.
Если возьмем параллелограмм и треугольник, то мы получим следующую
фигуру:
S
Полученная фигура называется
четырехугольной пирамидой.
Даная фигура состоит из:
параллелограмма,
являющегося основанием пирамиды, 4-х
треугольников, являющихся так же ее
гранями.
В данной фигуре 5-ть вершин и 8 ребер.
Обозначается
A
C
B
D
Если возьмем шестиугольник и треугольник, то мы получим следующую
фигуру:
S
Получили фигуру, которая называется
правильной шестиугольной пирамидой.
В состав ее входят:
правильный шестиугольник,
являющийся основанием пирамиды,
6-ть треугольников, причем все
треугольники равнобедренные и
равны между собой.
A
F
Данная пирамида имеет:
7 вершин,
6 граней
B 12 ребер
Обозначается
E
D
C
Если возьмем шестиугольник и прямоугольник, то мы получим следующую
фигуру:
A
B
C
F
E
A1
D
B1
Построенная фигура называется
шестиугольной призмой.
Она состоит из:
2-х оснований, являющихся
правильными шестиугольниками,
6-ти граней – прямоугольников.
Так же у данной фигуры 18 ребер и 12
вершин.
C1
F1
E1
D1
Обозначается
Мы построили и охарактеризовали ряд фигур. Давайте
сделаем из всех характеристик вывод и попробуем их
объединить в какую-то группу, и дать этой группе
название.
Все фигуры составлены из разного вида и количества
многоугольников, являющихся гранями данной фигуры.
Данная характеристика объединяет все рассмотренные нами
фигуры.
Связи с этим какое мы можем дать всем этим фигурам
название?
Многогранники.
Хорошо, а теперь дадим определение многогранника.
Поверхность, составленную из многоугольников и
ограничивающую некоторое геометрическое тело,
будем называть многогранной поверхностью или
многогранником.
Мы дали определение многогранника. Многогранники состоят из
многоугольников, а каких видов бывают многоугольники?
Выпуклые, невыпуклые, правильные.
Давайте теперь вспомним определения перечисленных видов
многоугольников.
Какой многоугольник называется выпуклым?
Многоугольник называется выпуклым, если он лежит по одну сторону от
прямой проходящей через две его соседние вершины.
Например, такие как:
Хорошо. Какие многоугольники называются невыпуклыми?
Многоугольник называется невыпуклым, если он лежит по разные стороны от
прямой проходящей через две его соседние вершины.
Например, такие:
Какой многоугольник называется правильным?
Правильным многоугольником называется выпуклый многоугольник, у которого все
стороны равны и все углы равны.
Так как многоугольники бываю различных видов. Это означает, что бывают и
различные виды многогранников.
Например, такие:
Многогранники бывают выпуклыми и
невыпуклыми. Выпуклый многогранник
расположен по одну сторону от
плоскости каждой своей грани.
Выпуклый
многогранник
Невыпуклый многогранник
расположен по разные
стороны от одной из
плоскости.
Невыпуклый
многогранник
Теперь рассмотрим некоторые виды многогранников
поподробнее.
Для начала дадим определение правильного
многогранника.
Правильным называется многогранник, у которого
все грани являются правильными многоугольниками,
и все многогранные углы при вершинах равны.
Существует 5-ть правильных многогранника.
1). Куб (гексаэдр)
2). Тетраэдр
3). Октаэдр
4). Икосаэдр
5). Додекаэдр
КУБ
A
D
B
C
B1
A1
D1
C1
Правильный
многогранник, у которого
грани – квадраты и в
каждой вершине сходится
по три ребра и три грани.
Состоит из:
6 граней,
8 вершин
12 ребер.
Обозначается
ТЕТРАЭДР
S
A
C
Правильный многогранник,
у которого грани
правильные треугольники
и в каждой вершине
сходится по три ребра и
по три грани.
Состоит из:
4 грани,
4 вершины,
6 ребер.
Обозначается
B
ОКТАЭДР
A
E
B
C
D
F
Правильный многогранник, у
которого граниправильные треугольники
и в каждой вершине
сходится по четыре ребра
и по четыре грани.
Состоит из:
8 граней,
6 вершин,
12 ребер
Обозначается
S
ИКОСОЭДР
A
D
E
B
C
D1
C1
E1
A1
B1
Правильный
многогранник, у которого
грани - правильные
треугольники и в вершине
сходится по пять рёбер и
граней.
Состоит из:
12 вершин,
20 граней,
30 ребер
Обозначается
S1
Додекаэдр
A1
A2
A5
A6
A4
A3
A8
A20
A10
A9
A7
A11
A17
A12
A13
Правильный многогранник,
у которого грани
правильные пятиугольники
A19
и в каждой вершине
сходится по три ребра и три
грани.
Состоит из:
20 вершин
A18 12 граней,
30 ребер.
Обозначается
A16
A14
A15
Как вы думаете где могут в жизни
встречаются многогранники?
В архитектуре, в украшениях.
Хорошо, давайте посмотрим на примеры
многогранников, которые встречаются в
жизни. Например, в архитектуре.
Башня Сююмбике
Башня Сююмбике
состоит из семи
ярусов, нижние ярусы
представляют из себя
параллелепипеды а
верхние многогранники.
Мечеть
Кул-Шариф
Архитектура этой мечети
представляет собой
сочетание различных
многогранников.
Никольский собор
Нижние ярусы
представляют собой
параллелепипеды, а
верхний ярус –
многогранник.
Спасская башня Кремля
Четыре яруса башни
представляют из себя
куб, многогранники и
пирамиду
Египетские пирамиды
Сальвадор Дали на картине “Тайная вечеря” изобразил И.Христа со своими
учениками на фоне огромного прозрачного додекаэдра.
Кристаллы белого фосфора
образованы молекулами Р4 . Такая
молекула имеет вид тетраэдра.
Фосфорноватистая кислота Н 3РО2.
Строение молекулы
метана .
Кристаллы поваренной соли.
Правильная форма алмаза.
Леонардо да Винчи любил изготовлять из дерева каркасы
правильных многогранников и преподносить их в виде подарка
различным знаменитостям.
Задания:
1. Используя модели многогранников заполнить данную
таблицу .
Название
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр
Число
граней и
их форма
Число
ребер
Число
вершин
2. Проведем эксперимент со значениями, которые будут
записаны в таблице.
3. Составить развертки правильных многогранников.
4. Построение октаэдра вписанного в куб.
Задание №1.
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр
4
6
8
20
12
Число
ребер
6
12
12
30
30
Число
вершин
4
8
6
12
20
Название
Число
граней и
их форма
Задание №2.
Давайте сложим число граней с числом вершин.
Название
Тетраэдр
Куб
Октаэдр
Икосаэдр
Додекаэдр
Число
граней (Г)
4
6
8
20
12
Число
ребер (Р)
6
12
12
30
30
Число
вершин (В)
4
8
6
12
20
Число
граней и
вершин
(Г+В)
8
14
14
32
32
Какой вывод можно сделать из заполненной нами
таблицы?
Если от суммы граней и вершин отнять число ребер, то оно
равно 2.
Данная закономерность превращается в теорему
Эйллера.
Число вершин плюс число граней минус число
рёбер равно двум.
Задание №3.
Задание №3.
Построение правильного тетраэдра
вписанного в куб
В
D
C
A
Рассмотрим вершину куба А.
В ней сходятся три грани куба,
имеющие форму квадратов. В
каждом из этих квадратов
берем вершину
противоположную А,вершины куба В, С, D. Точки
А, В,С, D- являются
вершинами правильного
тетраэдра.
Звездчатый октаэдр- многогранник,
полученный продолжением граней
октаэдра.
• Объединением каких
двух многогранников
он является?
• Что является их
пересечением?
Выполнить самостоятельно построение
правильного октаэдра, вписанного в куб.
Итоги урока
•
•
•
•
Чему мы сегодня научились?
За чем нам это нужно?
Окружают ли нас многогранники?
Назовите формулу Эйлера?
Домашнее задание
• Построение куба вписанного в октаэдр.