doc, 436 кб

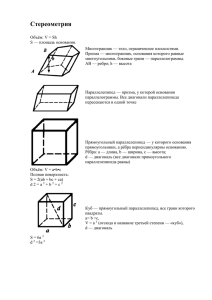
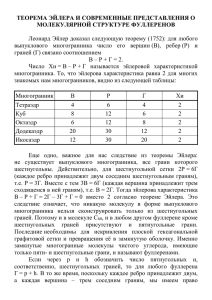
Задачи по олимпиаде 10 класс
1. Упростите выражение, указав при каких значениях a и b
упрощение возможно.
Решение: 1)
при a > 0, и b >0
2)
Ответ:
2. Доказать тождество:
.
Решение:
.
3. Решите неравенство:
.
Решение:
-1
y
0
1
x
0
1
такое
4. Найдите четыре целых числа, первые три из которых образуют
арифметическую прогрессию, а последние три – геометрическую; сумма
крайних чисел равна 66, а сумма средних равна 60.
Решение:
Ответ: 12; 24; 36; 54.
5. Длина стороны АВСД равна 6 см. Точка M удалена от каждой вершины
на 17 см. Найдите расстояние от середины отрезка MA до середины
каждой из сторон квадрата.
Решение: Рассмотрим треугольник АМВ, в нем КН – средняя линия,
поэтому
.
M
E
K
D
C
O
A
H
B
Проведем КЕ || AD, KECO – параллелограмм (КЕ || AD, AD || BC),
поэтому КЕ || OC; KE = OC = AD.
Применяя теорему косинусов для треугольника DMC и треугольника
EMC, находим DMC =
и EC = 9,5 см. Значит, и KO = 9,5 см.
Оставшиеся два расстояния от точки K до сторон AD и DC будут по 8,5
см и 9,5 см. Они находятся аналогично тому, как нашли KH и KO.
6. Футбольный мяч представляет собой многогранник с 32 гранями, 20 из
которых – белые правильные шестиугольники и 12 – черные правильные
пятиугольники. Сколько вершин у такого многогранника?
Решение: Так как между ребрами, гранями и вершинами выпуклого
многогранника есть связь, выражаемая формулой Эйлера: В+Г-Р=2, где
В – число вершин, Г – число граней, Р - число ребер, то В=Р+2-Г.
Граней у данного многогранника 32. Число ребер будет равно
. Тогда В=90+2-32=60. таким образом, многоугольник
имеет 60 вершин.
Ответ: 60